Péndulo de torsión

Procedimiento dinámico

En el procedimiento dinámico se separa la varilla soporte un cierto ángulo de suposición de equilibrio, se suelta, y la varilla comienza a oscilar.

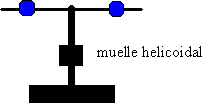
torsion1.gif (766 bytes)

A partir de la medida del periodo de las oscilaciones se obtiene la constante elástica del muelle.

Cuando la varilla soporte se ha desviado un ángulo θ y se suelta el muelle ejerce sobre la varilla soporte un momento -Kθ. El momento es de sentido contrario al desplazamiento angular.

Tenemos un sólido en rotación alrededor de un eje fijo bajo la acción de un momento. La ecuación de la dinámica de rotación se escribe

Iα =-Kθ .

En forma de ecuación diferencial

$\frac{d^{2} θ}{d t^{2}} + \frac{K}{I} θ = 0$

Esta es la ecuación diferencial de un MAS de frecuencia angular ω ²=K/I y periodo

$P = 2 π \sqrt{\frac{I}{K}}$

Ahora bien, el momento de inercia de la varilla soporte, del eje de rotación y del tornillo de sujeción no es conocido. Podemos superar este inconveniente, midiendo el periodo de las oscilaciones cuando la varilla tiene colocados dos cuerpos iguales de masa conocida, simétricamente dispuestos sobre la varilla.

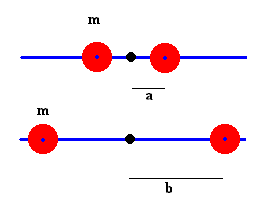
solido5.gif (942 bytes)

Cuando los cuerpos, en este caso esferas, están a una distancia a del eje, el momento de inercia es

$I_{a} = I_{var i l l a} + 2 I_{e s f e r a} + 2 m a^{2}$

El último término de la suma, proviene de la aplicación del teorema de Steiner.

El periodo de las oscilaciones vale

$P_{a}^{2} = 4 π^{2} \frac{I_{a}}{K}$

Cuando los cuerpos están a una distancia b del eje, el momento de inercia es

$I_{b} = I_{var i l l a} + 2 I_{e s f e r a} + 2 m b^{2}$

El periodo de las oscilaciones vale

$P_{b}^{2} = 4 π^{2} \frac{I_{b}}{K}$

Restando los cuadrados de ambos periodos se eliminan las cantidades desconocidas I_varilla e I_esfera

$P_{a}^{2} - P_{b}^{2} = \frac{8 π^{2} m}{K} (a^{2} - b^{2})$

Midiendo P_a y P_b despejamos de la fórmula la constante de torsión del muelle helicoidal K.

Completar una tabla como la siguiente, y calcular la constante de torsión K.

Masa de cada una de las esferas, m
Posición a
Periodo a
Posición b
Periodo b
Constante de torsión K

Actividades

Se introduce

Posición de a, en cm
Posición de b, en cm
Masa m de cada una de las esferas, en g

Se mide el periodo P_a de las oscilaciones del péndulo de torsión estando las esferas en la posición a. Aparece activado el correspondiente botón de radio.

Se cambia las esferas a la posición b, activando el botón de radio correspondiente. Se mide el periodo P_b de las oscilaciones del péndulo de torsión

Para que la precisión en la medidas sea mayor, se mide el periodo de varias oscilaciones (unas cinco) y se divide el tiempo total entre el número de oscilaciones.

Se pulsa en el botón titulado Empieza para que el péndulo comience a oscilar.

Para poner en marcha el cronómetro, se pulsa en el botón titulado En marcha. Para parar el cronómetro, se vuelve a pulsar en el mismo botón titulado ahora Parar.

Se obtiene numéricamente el valor de la constante de torsión y se compara con el resultado que nos proporciona el programa pulsando en el botón titulado Respuesta.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.