Anterior

Solución numérica

Para simplificar, tomemos una escala de tiempos tal que ξ=a2t, la ecuación diferencial que describe la conducción térmica se transforma en otra más sencilla.

∂T ∂ξ = ∂ 2 T ∂ x 2

La solución de la ecuación diferencial en derivadas parciales puede obtenerse utilizando el procedimiento de redes del siguiente modo

 

 

 

T

i

e

m

p

o

 Ta                             Tb
Ta                             Tb
Ta                             Tb
Ta                             Tb
Ta                             Tb
Ta                             Tb
Ta                             Tb
Ta                             Tb
Ta                             Tb
Ta                             Tb
Ta T0 T0 T0 T0 T0 T0 T0 T0 T0 T0 T0 T0 T0 T0 Tb
P o s i c i ó n

Consideremos un sistema de coordenadas posición – tiempo (x en el eje horizontal y x en el vertical). Construyamos un retículo trazando rectas paralelas al eje X equidistantes un intervalo fijo h y tal que h=L/n, siendo L la longitud de la barra y n el número de intervalos en los que se ha dividido la barra. Tracemos rectas paralelas al eje X, equidistantes una cantidad k.

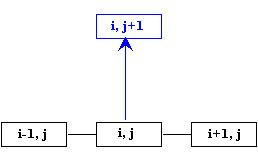Conduc_3.gif (1811 bytes)Podemos calcular la temperatura en los puntos de la barra x=ih (i=1, 2, 3, 4...n) y en el instante ξ=(j+1)k, a partir de los datos de la temperatura de la barra en los puntos x de la barra en el instante anterior ξ=jk (j=0, 1, 2, 3...) sin más que aplicar el procedimiento de recurrencia esquematizado en la figura, y cuya fórmula es

T i,j+1 = T i−1,j +4 T i,j + T i+1,j 6

La distribución inicial de partida (j=0) está dada por la temperatura inicial de la barra T0, y las temperaturas fijas en los extremos Ta y Tb a partir de las cuales y aplicando la fórmula de recurrencia, puede calcularse, sucesivamente, las temperaturas de cada una de los puntos de la malla (i, j).

Para practicar este método con una calculadora o con un pequeño programa de ordenador, se puede seguir el siguiente procedimiento:

  1. Constrúyase una tabla como la indicada y rellénese la columna izquierda, la columna derecha y la fila inferior con las temperaturas fijas en el extremo izquierdo de la barra Ta, del extremo derecho de la barra Tb, y con la temperatura inicial T0.
  1. Completar la primera fila vacía aplicando la fórmula de recurrencia. Las cifras obtenidas corresponden a la distribución de temperatura en un instante posterior al inicial.
  1. A partir de los datos de la primera fila, completar la segunda fila vacía, y así sucesivamente.
Anterior