La conducción del calor. Ley de Fourier
Introducción
El objetivo de este capítulo es el estudio de dos importantes fenómenos análogos:
- La transmisión del calor a lo largo de una barra metálica.
- La difusión unidimensional de un soluto en un disolvente.
Las leyes físicas que describen su comportamiento son simples y fácilmente comprensibles, pero la descripción analítica es compleja. Trataremos además, de resaltar las diferencias entre los mecanismos básicos que explican ambos fenómenos, y cómo afectan las condiciones de contorno a su evolución temporal. Así, en el problema de la conducción del calor a lo largo de una barra metálica se establecerán temperaturas fijas en los extremos de la barra, mientras que en el problema de la difusión se establecerá una masa de soluto en el origen de un medio unidimensional infinito en extensión.
Los fenómenos de transporte son aquellos procesos en los que hay una transferencia neta o transporte de materia, energía o momento lineal en cantidades grandes o macroscópicas. Estos fenómenos físicos tienen rasgos comunes que pueden ser descritos mediante la ecuación diferencial para la propagación unidimensional
Donde a es una constante característica de cada situación física y Ψ es el campo correspondiente al fenómeno de transporte de que se trata.
Históricamente, la ecuación que describe la difusión se denomina ley de Fick. El campo Ψ describe la concentración de soluto en el disolvente y la constante α=D, siendo D el coeficiente de difusión. La difusión se establece siempre que exista un gradiente o diferencia de concentración entre dos puntos del medio.
La ecuación que describe la conducción térmica se conoce como ley de Fourier, en este caso el campo Ψ es la temperatura T, y el coeficiente α=K/(ρc), donde K, es la conductividad térmica, ρ la densidad, y c es el calor específico del material. La conducción del calor se establece siempre que exista un gradiente o diferencia de temperaturas entre dos puntos de una barra metálica.
Se estudia cada uno de los fenómenos en dos partes:
- Se calcula la solución de la ecuación diferencial que gobierna el proceso.
- Se simulan los fenómenos a partir de mecanismos básicos simples. La simulación nos permitirá explicar las facetas esenciales de la descripción matemática del fenómeno en cuestión.
Ley de Fourier
Sea J la densidad de corriente de energía (energía por unidad de área y por unidad de tiempo), que se establece en la barra debido a la diferencia de temperaturas entre dos puntos de la misma. La ley de Fourier afirma que hay una proporcionalidad entre el flujo de energía J y el gradiente de temperatura.
Siendo K una constante característica del material denominada conductividad térmica.
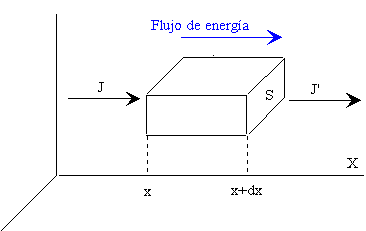
Consideremos un elemento de la barra de longitud dx y sección S. La energía que entra en el elemento de volumen en la unidad de tiempo es JS, y la que sale es J’S. La energía del elemento cambia, en la unidad de tiempo, en una cantidad igual a la diferencia entre el flujo entrante y el flujo saliente.
Esta energía, se emplea en cambiar la temperatura del elemento. La cantidad de energía absorbida o cedida (en la unidad de tiempo) por el elemento es igual al producto de la masa de dicho elemento por el calor específico y por la variación de temperatura.
Igualando ambas expresiones, y teniendo en cuenta la ley de Fourier, se obtiene la ecuación diferencial que describe la conducción térmica
Solución analítica
Supongamos una barra metálica de longitud L, conectada por sus extremos a dos focos de calor a temperaturas Ta y Tb respectivamente. Sea T0 la temperatura inicial de la barra cuando se conectan los focos a los extremos de la barra.
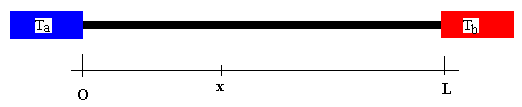
Al cabo de cierto tiempo, teóricamente infinito, que en la práctica depende del tipo de material que empleamos, se establece un estado estacionario en el que la temperatura de cada punto de la barra no varía con el tiempo. Dicho estado está caracterizado por un flujo J constante de energía. La ley de Fourier establece que la temperatura variará linealmente con la distancia x al origen de la barra.
Para describir el estado transitorio buscamos una solución de la forma T(x, t)=F(x)·G(t), variables separadas
El signo negativo asegura el carácter transitorio.
Integramos la primera ecuación diferencial
Integramos la segunda ecuación diferencial
Es una ecuación diferencial similar a la de un MAS, cuya solución es a·sen(ωx+δ)
La temperatura en cualquier punto x a lo largo de la barra, en un instante determinado, T(x, t) es la solución de la ecuación diferencial, que es una combinación de dos términos, la que corresponde al régimen permanente más la del régimen transitorio.
Condiciones de contorno
-
En x=0, T(0, t)=Ta, temperatura fija del extremo izquierdo de la barra
-
En x=L, T(L, t)=Tb, temperatura fija del extremo derecho de la barra
El régimen variable general de temperaturas de la barra es
Distribución inicial de temperaturas
Solamente, queda por determinar los coeficientes an, identificando esta solución con la distribución inicial de temperaturas en la barra T(x, 0)=T0 en el instante t=0.
Más abajo, se proporcionan los detalles del cálculo de los coeficientes an del desarrollo en serie al lector interesado.
La temperatura en cualquier punto de la barra x, en un instante t, se compone de la suma de un término proporcional a x, y de una serie rápidamente convergente que describe el estado transitorio.
El valor de α=K/(ρc) nos da una medida de la rapidez con la que el sistema alcanza el estado estacionario. Cuanto mayor sea α antes se alcanza el estado estacionario
Actividades
En este programa, estudiaremos la conducción del calor a lo largo de una barra metálica cuyos extremos están conectados a dos focos de calor que tienen distintas temperaturas. Observaremos la evolución de la temperatura de cada punto de la barra a medida que transcurre el tiempo.
Examinaremos los factores que determinan la conducción del calor a lo largo de una barra metálica, probando barras de distintos materiales, con distintas temperaturas fijas de los extremos e inicial de la barra.
- Se selecciona en el control selección el Metal de la barra. Las unidades de las magnitudes están expresadas en el Sistema Internacional de Unidades de Medida.
| Metal | Densidad | Calor específico | Conductividad térmica | α |
| Aluminio | 2700 | 880 | 209.3 | 8.81·10-5 |
| Acero | 7800 | 460 | 45 | 1.25·10-5 |
| Cobre | 8900 | 390 | 389.6 | 11.22·10-5 |
| Latón | 8500 | 380 | 85.5 | 2.65·10-5 |
| Plata | 10500 | 230 | 418.7 | 17.34·10-5 |
| Plomo | 11300 | 130 | 34.6 | 2.35·10-5 |
Fuente: Koshkin N. I., Shirkévich M. G.. Manual de Física Elemental. Editorial Mir 1975. págs 36, 74-75, 85-86
Se introduce, moviendo las flechas de color azul con el puntero del ratón
- La temperatura fija en el extremo izquierdo de la barra Ta.
- La temperatura fija en el extremo derecho de la barra Tb.
- La temperatura inicial de la barra T0.
- La longitud de la barra metálica se ha fijado en el valor de L=0.5 m.
Se pulsa el botón titulado Nuevo
- El instante t, en minutos, en el que queremos representar la distribución de temperaturas a lo largo de la barra, en el control de edición o actuando en la barra de desplazamiento titulada Tiempo.
Se pulsa en el botón titulado Gráfica.
El programa interactivo representa la distribución de temperaturas a lo largo de la barra, en el instante actual (en color rojo), y en el instante previamente introducido (en color azul).
Cuestiones:
- Examinar la evolución de la distribución de temperaturas con el tiempo. Comprobar que el régimen estacionario es independiente de la temperatura inicial, solamente depende de la temperatura de los focos frío y caliente.
- Examinar el comportamiento de barras hechas de distintos materiales, con la misma temperatura inicial y fijas en los extremos.
Arrastre con el puntero del ratón las flechas de color azul
Cálculo de los coeficientes del desarrollo en serie an
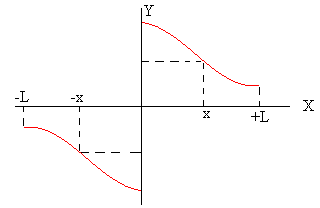 |
La parte derecha de la igualdad es el desarrollo en serie de una función f(x) impar, ya que carece del término independiente y de los términos en coseno. El periodo de f(x) es 2L y se extiende desde –L a +L tal como se muestra en la figura. |
Multiplicamos ambos miembros por sen(mπx/L) e integramos entre –L y +L
Efectuamos el cambio de variable z=πx/L, dz= πdx/L
(1)
Integramos por partes la integral que aparece en el segundo miembro
Volvemos a integrar por partes
Cuando m=n
La expresión (1) se simplifica notablemente
Supongamos que la temperatura inicial de la barra en todos sus puntos es la misma T(x, 0)=T0, la función f(x) es lineal
Calculamos los coeficientes an del desarrollo en serie de Fourier
Finalmente,
Referencias
Puig Adam P., Curso teórico-práctico de ecuaciones diferencias aplicado a la Física y Técnica. Biblioteca Matemática (1950), págs. 300-303
