• Inicio
• Fenómenos de transporte
• Conducción del calor

Ondas térmicas

En esta página, se describe un experimento que nos permite estudiar la propagación de las ondas térmicas a lo largo de una barra de metal.

Como aplicación, citaremos que las variaciones diurnas  de temperatura penetran en el suelo más rápidamente pero con menor profundidad que las variaciones anules de temperatura debidos a los cambios de estación. Se puede explicar este fenómeno en términos de la velocidad de propagación y del amortiguamiento de la amplitud de la onda térmica que dependen de su frecuencia.

 

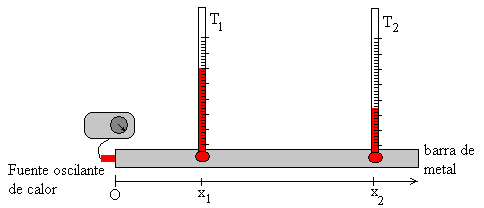
Se calienta el extremo de una barra de cobre de L=50 cm de longitud de forma periódica con un soldador conectado a un reloj. Después de comenzar el experimento, se deja pasar cierto tiempo hasta que se alcanza un estado de equilibrio dinámico en el que las temperaturas de cada punto de la barra oscilan alrededor de sus valores medios.

Se miden las temperaturas en dos puntos situados a una distancia x₁ y x₂ del origen de la barra. La relación entre las amplitudes de la oscilación térmica nos va proporcionar el valor del coeficiente de amortiguamiento y la diferencia de fase, la velocidad de propagación de las ondas térmicas en la barra. La relación entre estos dos parámetros nos proporciona el coeficiente α de la ecuación que describe la conducción térmica.

${\displaystyle \frac{\partial T}{\partial t}=\alpha \frac{{\partial }^{2}T}{\partial x^2}\alpha =\frac{K}{\rho c}}$

donde α es un coeficiente que depende de la densidad ρ, calor específico c y conductividad térmica K del metal.

Calentamiento del extremo de la barra

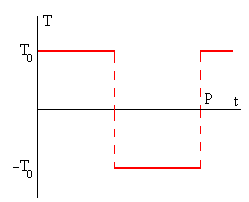El calentamiento en el extremo de la barra x=0, se puede describir mediante un pulso periódico, de periodo P, en forma de escalón de altura 2·T0, tal como se aprecia en la figura. Esta función, se puede expresar en términos de un desarrollo en serie de Fourier, los detalles se pueden consultar en cualquier libro de Cálculo integral.

Si f(t) es una función periódica de periodo P, se puede expresar en forma de desarrollo en serie de la forma.

${\displaystyle f(t)=\frac{a_0}{2}+{\displaystyle \sum _{i=1}^{\infty }\left(a_i\cos \left(i\frac{2\pi }{P}t\right)+b_i\text{sin}\left(i\frac{2\pi }{P}t\right)\right)}}$

donde

${\displaystyle \begin{array}{l}\frac{a_0}{2}=\frac{2}{P}{\displaystyle \underset{0}{\overset{P}{\int }}f(t)·dt}\\ a_i=\frac{2}{P}{\displaystyle \underset{0}{\overset{+P}{\int }}f(t)\cos \left(i\frac{2\pi }{P}t\right)·dt}i=\mathrm{1,}\text{ 2}\text{, 3}\mathrm{...}\\ b_i=\frac{2}{P}{\displaystyle \underset{0}{\overset{+P}{\int }}f(t)\sin \left(i\frac{2\pi }{P}t\right)·dt}i=\mathrm{1,}\text{ 2}\text{, 3}\mathrm{...}\end{array}}$

Para un escalón de potencial

f(t)=T₀ para 0≤t<P/2
f(t)=-T₀ para P/2≤t<P

Los coeficientes a_i y b_i de Fourier valen

${\displaystyle \begin{array}{l}{a}_0=\frac{2}{P}\left({\displaystyle \underset{0}{\overset{P/2}{\int }}{T}_0·dt}+{\displaystyle \underset{P/2}{\overset{P}{\int }}(-T_0)·dt}\right)=0\\ a_i=\frac{2}{P}\left({\displaystyle \underset{0}{\overset{P/2}{\int }}{T}_0·\cos \left(i\frac{2\pi }{P}t\right)dt}+{\displaystyle \underset{P/2}{\overset{P}{\int }}(-T_0)\cos \left(i\frac{2\pi }{P}t\right)·dt}\right)=\frac{T_0}{i·\pi }\left({\left[\sin \left(i\frac{2\pi }{P}t\right)\right]}_0^{P/2}-{\left[\sin \left(i\frac{2\pi }{P}t\right)\right]}_{P/2}^P\right)=0\\ b_i=\frac{2}{P}\left({\displaystyle \underset{0}{\overset{P/2}{\int }}{T}_0·\sin \left(i\frac{2\pi }{P}t\right)dt}+{\displaystyle \underset{P/2}{\overset{P}{\int }}(-T_0)\sin \left(i\frac{2\pi }{P}t\right)·dt}\right)=\frac{T_0}{i·\pi }\left({\left[\text{-cos}\left(i\frac{2\pi }{P}t\right)\right]}_0^{P/2}+{\left[\text{cos}\left(i\frac{2\pi }{P}t\right)\right]}_{P/2}^P\right)\end{array}}$

El resultado de la integral es

${\displaystyle \begin{array}{l}{a}_i=0i=\text{0}\text{, 1}\text{, 2}\mathrm{...}\\ b_i=0i=\text{2}\text{, 4}\text{, 6}\mathrm{...}\\ b_i=\frac{4T_0}{i·\pi }i=\text{1}\text{, 3}\text{, 5}\mathrm{...}\end{array}}$

El desarrollo en serie de la función escalón es

${\displaystyle f(t)={\displaystyle \sum _{i=\mathrm{1,3,5...}}^{\infty }\frac{4T_0}{i·\pi }\sin \left(i\frac{2\pi }{P}t\right)}}$

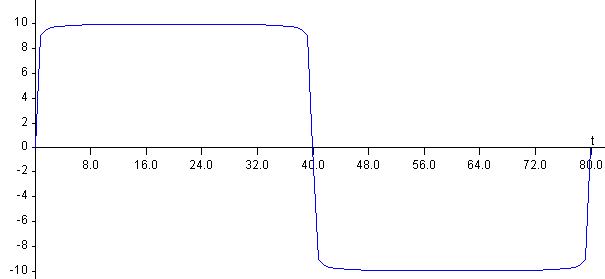
En la figura, se representa el calentamiento del extremo de la barra x=0, descrito por una función escalón de periodo P=80 s y cuya amplitud es de T₀=10º C.

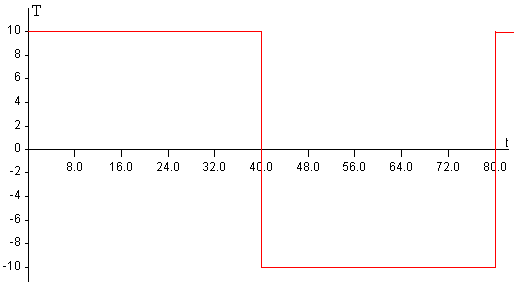
En la figura, se muestra la aproximación a la función escalón tomando los cinco primeros términos i=1, 3, 5, 7, y 9 del desarrollo en serie

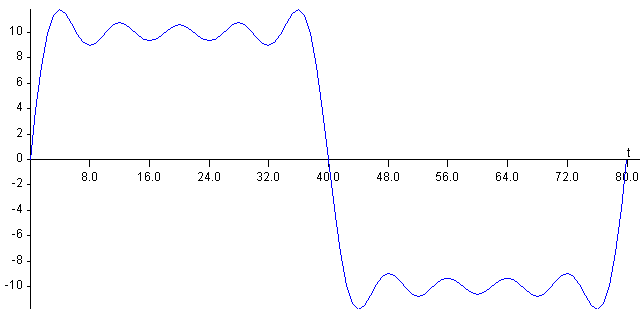
En esta otra figura, la aproximación a la función periódica tomando los 50 primeros términos cuyos índices i son los números impares que van desde i=1 a 99.

Propagación de la onda térmica

La distribución de temperaturas en la barra después de un tiempo de haber comenzado el experimento, cuando el sistema haya olvidado las condiciones iniciales, está dada por una serie, cada uno de cuyos términos corresponde a una onda armónica de frecuencia angular ω_i, número de onda k_i y velocidad de propagación v_i=ω_i/k_i.

${\displaystyle T(x,t)={\displaystyle \sum _{i=1}^{\infty }{A}_i(x)\sin ({\omega }_{i}t-k_{i}x)}}$

Introduciendo esta solución en la ecuación que describe la conducción térmica

${\displaystyle \frac{\partial T}{\partial t}=\alpha \frac{{\partial }^{2}T}{\partial x^2}\alpha =\frac{K}{\rho c}}$

se obtiene

${\displaystyle {\displaystyle \sum _{i=1}^{\infty }\left(\frac{{\partial }^2{A}_i}{\partial x^2}-k_i^2{A}_i\right)}\sin ({\omega }_{i}t-k_{i}t)-{\displaystyle \sum _{i=1}^{\infty }\left(2\frac{\partial A_i}{\partial x}{k}_i+\frac{{\omega }_i}{\alpha }{A}_i\right)}\text{cos}({\omega }_{i}t-k_{i}t)=0}$

La igualdad a cero, conduce al sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}2\frac{\partial A_i}{\partial x}{k}_i+\frac{{\omega }_i}{\alpha }{A}_i=0\\ \frac{{\partial }^2{A}_i}{\partial x^2}-k_i^2{A}_i=0\end{array}}$

Con la condición inicial en el extremo x=0 de la barra

${\displaystyle T(\mathrm{0,}t)={\displaystyle \sum _{i=\mathrm{1,3,5...}}^{\infty }\frac{4T_0}{i·\pi }\sin \left(i\frac{2\pi }{P}t\right)}={\displaystyle \sum _{i=\mathrm{1,3,5...}}^{\infty }\frac{4T_0}{i·\pi }\sin \left({\omega }_{i}t\right)}}$

Integramos la primera ecuación diferencial

${\displaystyle \frac{d{A}_i}{A_i}=-\frac{{\omega }_i}{2\alpha k_i}dx}$

con la condición inicial de que en x=0, A_i(0)=4·T₀/(i·π). La solución es

${\displaystyle A_i(x)=\frac{4T_0}{i·\pi }\exp \left(-\frac{{\omega }_i}{2\alpha k_i}x\right)}$

Introduciendo A_i(x) en la segunda ecuación diferencial

${\displaystyle {\left(-\frac{{\omega }_i}{2\alpha k_i}\right)}^2{A}_i-k_i^2{A}_i=0k_i=\sqrt{\frac{{\omega }_i}{2\alpha }}}$

La amplitud A_i(x) decrece exponencialmente con la distancia x a la fuente de calor de la forma

${\displaystyle A_i(x)=\frac{4T_0}{i·\pi }\exp \left(-k_{i}x\right)}$

La distribución de temperaturas para cada punto x de la barra en función del tiempo t es

${\displaystyle T(x,t)={\displaystyle \sum _{i=1}^{\infty }\frac{\text{4}{T}_0}{i·\pi }\text{exp(-}{k}_{i}x\text{)·sin}({\omega }_{i}t-k_{i}x)}{k}_i=\sqrt{\frac{{\omega }_i}{2\alpha }}{\omega }_i=i\frac{2\pi }{P}}$

La amplitud A_i(x) decrece rápidamente con x y también con i.  Los armónicos altos desaparecen, quedando lejos de la fuente tan solo el primer armónico i=1. La distribución de temperaturas para esos puntos se puede describir mediante la ecuación

${\displaystyle T(x,t)\approx \frac{\text{4}{T}_0}{\pi }\text{exp(-}k·x\text{)·sin}(\omega t-kx)k=\sqrt{\frac{\omega }{2\alpha }}\omega =\frac{2\pi }{P}}$

La velocidad de propagación de las ondas térmicas en la barra de metal vale

${\displaystyle v=\frac{\omega }{k}=\sqrt{2\alpha \omega }}$

Cuando la velocidad de propagación v depende de la frecuencia ω, el medio se dice que es dispersivo.

El cociente v/(2k)=α que es un parámetro característico de cada metal en el proceso de conducción térmica.

Medida del coeficiente k de amortiguamiento de la amplitud

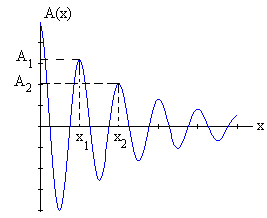
Como hemos demostrado, la amplitud de la onda armónica decrece exponencialmente con la distancia x a la fuente de calor situada en el extremo de la barra.

${\displaystyle A(x)=\frac{4T_0}{\pi }\exp (-kx)}$

Colocamos dos termómetros a las distancias x₁ y x₂ lejos de la fuente de calor, para que la aproximación anterior sea válida.

Medimos la amplitud A1 de la oscilación de la temperatura en la posición x1 Medimos la amplitud A2 de la oscilación de la temperatura en la posición x2

${\displaystyle \frac{A_2}{A_1}=\exp \left(-k(x_2-x_1)\right)k=\frac{1}{\Delta x}\ln \frac{A_1}{A_2}}$

Medida de la velocidad de propagación

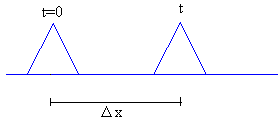Cuando se propaga un Movimiento Ondulatorio, la perturbación, un pico, un valle, se desplaza una longitud Δx en un tiempo Δt. Si el máximo de temperatura  en el punto x₁ se produce en el instante t₁ y el máximo de temperatura en el punto x₂ se produce en el instante t₂. La velocidad de propagación v de las ondas térmicas, se obtiene mediante el cociente

${\displaystyle v=\frac{x_2-x_1}{t_2-t_1}=\frac{\Delta x}{\Delta t}}$

Tres velocidades caracterizan otros tantos procesos en un metal:

• La velocidad del sonido, que depende del módulo de Young y de la densidad del material, del orden de 3000 m/s para el cobre.

• La velocidad de los electrones del conducción del orden de 4·10^-7 m/s

• La velocidad de propagación de las ondas térmicas, del orden de 3·10^-3 m/s

Actividades

Se pulsa el botón titulado Nuevo

Con el puntero del ratón se mueven las flechas de color rojo y de color azul a posiciones marcadas en cm en la regla. Las flechas representan termistores (termómetros) previamente calibrados. Las medidas de resistencia eléctrica se convierten en medidas precisas de temperatura, que se muestran en la parte superior del applet.

Se introduce

• El material del que está hecha la barra, en el control de selección titulado Metal.

• La amplitud T₀ de la oscilación de la temperatura en el extremos de la barra x=0, actuando en la barra de desplazamiento titulada Amplitud temperatura.

• El periodo de la oscilación P en segundos, en el control de edición titulado Periodo.

Se pulsa el botón titulado Empieza

Se observa, que durante medio periodo el extremo de la barra se calienta (color rojo) y durante el otro medio periodo se enfría (color azul). Encima del extremo de la barra aparece un reloj conectado a un dispositivo que calienta o enfría dicho extremo.

Las curvas en color rojo y azul corresponden a las oscilaciones de temperatura en las posiciones que ocupan la flecha roja y azul. Si la amplitud de las oscilaciones es pequeña, se puede aumentar la escala de la representación gráfica en el control de selección titulado Escala.

Las posiciones de las flechas (termistores)  se elegirán de modo que las oscilaciones de temperatura en dichos lugares se describan aproximadamente mediante un MAS.

• Se mide la temperatura máxima o mínima A₁ y A₂, y se calcula el coeficiente k de amortiguamiento de la amplitud.

• Se mide la diferencia de tiempos Δt, que tarda el máximo o el mínimo en desplazarse desde la posición x₁ a la posición x₂, es decir, Δx=x₂-x₁

Ejemplo:

• El metal de la barra es cobre

• La amplitud de proceso de calentamiento-enfriamiento del extremo de la barra es T₀=15º

• El periodo es P=80 s

Observamos que en las posiciones x₁=15 cm y x₂=25 cm las oscilaciones de temperatura se describen aproximadamente mediante un MAS.

 

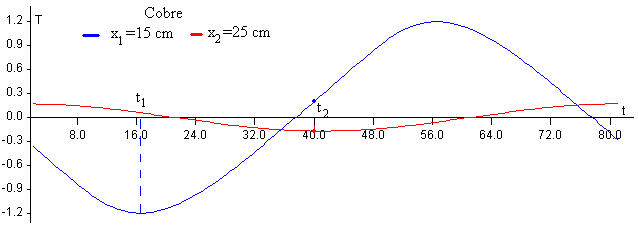
Se elige la escala 10 de la representación gráfica, para realizar mejor las medidas.

• En la posición x₁=15 cm se alcanza el mínimo de temperatura en el instante t₁=15.0, la temperatura mínima es A₁=1.201

• En la posición x₂=25 cm se alcanza el mínimo de temperatura en el instante t₂=39.5, la temperatura mínima es A₂=0.176.

El coeficiente k de amortiguamiento de la amplitud de la onda térmica vale

${\displaystyle k=\frac{1}{\Delta x}\ln \frac{A_1}{A_2}k=\frac{1}{(0.25-0.15)}\ln \frac{1.201}{0.176}=19.2{\text{m}}^{\text{-1}}}$

La velocidad de propagación de las ondas térmicas en la barra de cobre es

${\displaystyle v=\frac{x_2-x_1}{t_2-t_1}v=\frac{0.25-0.15}{39.5-15.0}=4.08·{10}^{-3}\text{m/s}}$

Calculamos el cociente

${\displaystyle \frac{v}{2k}=\alpha \frac{4.08·{10}^{-3}}{2·19.2}=10.62·{10}^{-5}{\text{m}}^{\text{2}}\text{/s}}$

Comprobación

Los datos para el cobre son

• Densidad ρ=8900 kg/m³

• Calor específico c=390 J/(kg·K)

• Conductividad térmica K=389.6 W/(m·K)

El valor de α=K/(ρ·c)=11.22·10^-5 m²/s

TermicoApplet3 aparecerá en un explorador compatible con JDK 1.1.

Se arrastra con el puntero del ratón las fechas de color rojo y azul

Referencias

Bodas A, Gandía V., E. López-Baeza. An undergraduate experiment on the propagation of thermal waves. Am. J. Phys. 66 (6) June 1998, pp. 528-533.

Curso Interactivo de Física en Internet © Ángel Franco García