Asignatura de libre elección

Creación de Contenidos Interactivos en Internet

1.-Crear una clase denominada Lista cuyo miembro dato sea un array de números enteros y cuyas funciones miembro realicen las siguientes tareas:

• Hallar y devolver el valor mayor
• Hallar y devolver el valor menor
• Hallar y devolver el valor medio
• Ordenar los números enteros de menor a mayor
• Mostrar la lista ordenada separando los elementos por un tabulador

Hacer el ejercicio y comprobar la solución en la página: www.sc.ehu.es/sbweb/fisica/cursoJava/fundamentos/clases1/poo1.htm

2.-Crear una clase denominada Estadistica, que calcule y devuelva la media aritmética, la desviación media y la desviación estándar.

Una de las medidas que caracterizan a una distribución es la media aritmética, que se obtiene sumando los valores x_i introducidos, y dividiendo entre el número total N.

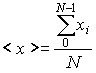
Se denomina desviación, a la diferencia entre un valor y la media aritmética de la serie estadística, d_i=x_i-<x>. La desviación media es la media aritmética de los valores absolutos de todas las desviaciones. Su fórmula es

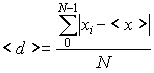
La desviación cuadrática media es la raíz cuadrada de la varianza, es decir, de la media aritmética de los cuadrados de las desviaciones respecto a la media.

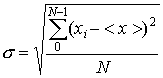
Hacer el ejercicio y comprobar su solución en la página: www.sc.ehu.es/sbweb/fisica/cursoJava/numerico/regresion/estadistica.htm

En la página www.sc.ehu.es/sbweb/fisica/unidades/medidas/medidas.htm hay un applet que realiza estos cálculos

3.-Crear una clase denominada Regresion que calcule la ecuación de la recta de regresión y=ax+b, (pendiente a y ordenada en el origen b) y el coeficiente de correlación r.

Leer la teoría en el primer apartado de la página www.sc.ehu.es/sbweb/fisica/cursoJava/numerico/regresion/regresion.htm, resolver el problema y comprobar en dicha página la solución correcta.

En la página www.sc.ehu.es/sbweb/fisica/cinematica/regresion/regresion.htm se explica el concepto de regresión lineal y en la página www.sc.ehu.es/sbweb/fisica/cinematica/practica/practica.htm se aplica al cálculo de la velocidad de un móvil en movimiento rectilíneo y uniforme.

4.- Obtener el triángulo de Tartaglia

Los números que aparecen en cada fila son los coeficientes del desarrollo del binomio de Newton con n=0, 1, 2, 3, 4, ... Fijarse en la ley de composición,  El número 4 de la última fila se obtiene sumando el número que le precede 3 y el que le sigue 1 de la fila anterior.

1. Definir una función que devuelva un array que contenga los coeficientes de una fila cuando se le siuministra el número n.
2. Definir una función que calcule y devuelva la potencia entera de un número real.
3. Usar ambas funciones para crear otra función que imprima los coeficientes del polinomio , donde a es un número real cualquiera, 3, 0.5, -1, etc. que se le pasa a dicha función.

Los números combinatorios son los que se obtienen mediante la primera función, la que obtiene las filas del triángulo de Tartaglia.

Esquema de la aplicación:

public class BinomioApp {
    static double potencia(double base, int exponente){
	//...
    }
    static int[] tartaglia(int n){
	//....
    }
    static void coefPolinomio(int n, double a){
	//...
        for(int i=n; i>=0; i--){
		//calcula e imprime los coeficientes del polinomio           
        }
    }

    public static void main(String[] args) {
        coefPolinomio(4, 2); //polinomio de grado 4

         try  {
//espera la pulsación de RETORNO
            System.in.read();
        }catch (Exception e) {  }

    }

}