Asignatura de libre elección

Creación de Contenidos Interactivos en Internet

1.- Crear una clase denominada Matematicas que defina las siguientes funciones estáticas

• Calcule y devuelva el valor absoluto de un número entero
• Calcule y devuelva la potencia entera de un número entero
• Calcule el factorial de un número
• Determine si un número entero es o no primo

Hacer el ejercicio y comprobar la solución en la página www.sc.ehu.es/sbweb/fisica/cursoJava/fundamentos/estatico/mates/mates.htm

2.-Obtener las sucesivas aproximaciones del número irracional PI.mediante la fórmula

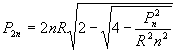
Tomando como radio R, la unidad

• Para un triángulo, n=3, el perímetro
• Para un hexágono, n=6, el perímetro P₆=6.
• y así sucesivamente.

Para obtener las sucesivas aproximaciones del número irracional p mediante la fórmula anterior procedemos del siguiente modo

1. Partimos del valor del perímetro P de un triángulo equilátero inscrito en una circunferencia de radio unidad, el valor de n es 3.
2. Calculamos el perímetro P de un polígono de 2n lados a partir del valor del perímetro de un polígono regular de n lados.
3. El valor obtenido P será el valor del perímetro de un polígono regular de n=2n lados.
4. Se imprime el valor de P dividido entre dos (aproximación de p)
5. Se vuelve al paso 2.

Hacer el ejercicio y comprobar su solución en la página www.sc.ehu.es/sbweb/fisica/cursoJava/fundamentos/fundamentos/estatico/math/math.htm

3.- El desarrollo en serie de sen x es

Comparar el valor obtenido por la función Math.sin(Math.PI/4) seno de 45º, con el valor obtenido al sumar un número determinado (10, 20, etc.) de términos del desarrollo en serie. Hacer lo mismo para 30º o Math.PI/6.

En el desarollo en serie

Tomando x=1, comparar el valor del número e dado por Math.E con el valor obtenido al sumar un número determinado (10, 20, etc.) de términos del desarrollo en serie.

4.- Estudiar la clase Fraccion y crear una clase similar denominada Complejo con las siguientes funciones miembro

• Dos constructores, uno por defecto (sin parámetros)  y otro explícito.
• Redefinir toString para mostrar un número complejo
• Dos funciones que devuelvan el módulo y el argumento de un número complejo
• Funciones que estáticas que realicen las siguientes operaciones
• Suma de dos números complejos
• Producto de dos números complejos
• Producto de un número complejo por un número real con el mismo nombre que la anterior
• Cociente de dos números complejos
• Cociente de un número complejo entre un número real con el mismo nombre
• Potencia de un número complejo

No olvidarse de poner delante de los miembros dato y de los miembros función los modificadores de acceso public y private.

Hacer el ejercicio y comprobar la solución en la página www.sc.ehu.es/sbweb/fisica/cursoJava/numerico/complejo/complejo.htm

5.-Crear una clase denominada Vector3D en el espacio (tres componentes) que defina dos operaciones el producto escalar y el producto vectorial de dos vectores. Finalmente, redefinir la función toString para mostrar el vector.

4.- Definir una clase denominada Vector que representa a un vector de dimensión n. Definir una clase denominada Matriz, que representa una matriz cuadrada de dimensión n. Definir en dicha clase las siguientes operaciones como funciones estáticas

• Suma de dos matrices de las mismas dimensiones
• Producto de dos matrices de las mismas dimensiones
• Producto de una matriz por un vector de las mismas dimensiones
• Producto de un vector por una matriz
• Producto de un número real por una matriz

Redefinir en ambas clases toString para mostrar el vector y la matriz respectivamente.

Hacer el ejercicio y comprobar su solución en la página www.sc.ehu.es/sbweb/fisica/cursoJava/numerico/matrices/matriz/matriz.htm