Ecuaciones diferenciales |
Sistema de dos ecuaciones diferenciales de segundo orden
Sea el sistema de dos ecuaciones diferenciales de segundo orden
![]()
![]()
con las condiciones iniciales
![]()
Este sistema, se puede transformar en un sistema equivalente formado por cuatro ecuaciones diferenciales de primer orden. Aplicando dos veces el esquema descrito para una ecuación diferencial de segundo orden, obtenemos el esquema descrito en las siguientes tablas
|
|
|
|
La codificación de la función que resuelve el sistema de dos ecuaciones diferenciales de segundo orden, repite dos veces, el código de la función resolver correspondiente a una ecuación diferencial de segundo orden, ya que hay que calcular cuatro pares de parámetros más, los correspondientes a la segunda ecuación diferencial de segundo orden.
De modo análogo a los apartados anteriores, estableceremos una jerarquía de clases, la clase base abstracta define el procedimiento numérico y la clase derivada define el sistema físico particular.
public abstract class RungeKutta {
public void resolver(double tf, Estado e, double h){
//variables auxiliares
double k1, k2, k3, k4;
double l1, l2, l3, l4;
double q1, q2, q3, q4;
double m1, m2, m3, m4;
//estado inicial
double x=e.x;
double y=e.y;
double vx=e.vx;
double vy=e.vy;
double t0=e.t;
for(double t=t0; t<tf; t+=h){
k1=h*vx;
l1=h*f(x, y, vx, vy, t);
q1=h*vy;
m1=h*g(x, y, vx, vy, t);
k2=h*(vx+l1/2);
l2=h*f(x+k1/2, y+q1/2, vx+l1/2, vy+m1/2, t+h/2);
q2=h*(vy+m1/2);
m2=h*g(x+k1/2, y+q1/2, vx+l1/2, vy+m1/2, t+h/2);
k3=h*(vx+l2/2);
l3=h*f(x+k2/2, y+q2/2, vx+l2/2, vy+m2/2, t+h/2);
q3=h*(vy+m2/2);
m3=h*g(x+k2/2, y+q2/2, vx+l2/2, vy+m2/2, t+h/2);
k4=h*(vx+l3);
l4=h*f(x+k3, y+q3, vx+l3, vy+m3, t+h);
q4=h*(vy+m3);
m4=h*g(x+k3, y+q3, vx+l3, vy+m3, t+h);
x+=(k1+2*k2+2*k3+k4)/6;
vx+=(l1+2*l2+2*l3+l4)/6;
y+=(q1+2*q2+2*q3+q4)/6;
vy+=(m1+2*m2+2*m3+m4)/6;
}
//estado final
e.x=x;
e.y=y;
e.vx=vx;
e.vy=vy;
e.t=tf;
}
abstract public double f(double x, double y, double vx, double vy, double t);
abstract public double g(double x, double y, double vx, double vy, double t);
}
|
El estado del sistema vendrá dado por cuatro números x, y, vx, vy y t, miembros dato de la clase que hemos denominado Estado.
public class Estado {
public double t;
public double x;
public double y;
public double vx;
public double vy;
public Estado(double t, double x, double y, double vx, double vy) {
this.t=t;
this.x=x;
this.y=y;
this.vx=vx;
this.vy=vy;
}
}
|
Uno de los ejemplos más interesantes de resolución de un sistema de ecuaciones diferenciales de segundo orden es la descripción del movimiento de los planetas, el cual tiene una solución analítica sencilla en coordenadas polares. La trayectoria seguida por un planeta es una cónica, una elipse en particular, en uno de cuyos focos está el centro fijo de fuerzas, el Sol. En la figura, se muestra la fuerza que ejerce el Sol sobre un planeta, inversamente proporcional al cuadrado de las distancias que separan sus centros, y también se muestran sus componentes rectangulares
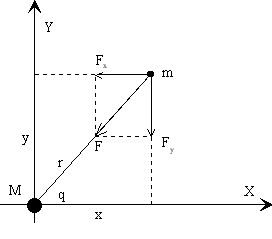
Teniendo en cuenta que la fuerza que ejerce el sol sobre un planeta viene descrita por la ley de la Gravitación Universal
![]()
donde M es la masa del Sol, m la masa del planeta y r la distancia entre el centro del Sol y del planeta. Las componentes de la aceleración del planeta serán
![]()
![]()
Uno de los problemas del tratamiento numérico con ordenador, es la de reducir el problema a números simples e inteligibles por el usuario de un vistazo. Las masa de los planetas y del Sol son números muy grandes: la masa de la Tierra es 5.98 1024 kg., y 1.98 1030 kg. la del Sol. La distancia media entre la Tierra y el Sol es también muy grande 1.49 1011 m. y la constante G es muy pequeña 6.67 10-11 en el Sistema Internacional de Unidades. Podemos simplificar el problema numérico, refiriéndonos a un hipotético Sol cuya masa sea tal que el producto GM=1 o bien, que se ha cambiado la escala de los tiempos de modo que se cumpla esta condición. Teniendo en cuenta que la aceleración es la derivada segunda de la posición, el sistema de dos ecuaciones diferenciales de segundo orden quedará
![]()
![]()
En la clase derivada Planeta redefinimos las funciones f y g.
public class Planeta extends RungeKutta{
public double f(double x, double y, double vx, double vy, double t){
double r=Math.sqrt(x*x+y*y);
return (-x/(r*r*r));
}
public double g(double x, double y, double vx, double vy, double t){
double r=Math.sqrt(x*x+y*y);
return (-y/(r*r*r));
}
}
|
Los pasos para usar la clase Planeta son los siguientes
- Establecer la magnitud del paso h
- Introducir el estado inicial de la partícula (su posición y su velocidad inicial)
- Establecer el tiempo final t, en el que deseamos calcular el nuevo estado del planeta.
- Crear un objeto de la clase Planeta y llamar a la función miembro resolver.
- Mostrar la posición y velocidad final del planeta.
double h=0.1; //paso
//Situación inicial
double x0=1.0;
double vy0=1.2;
Estado es=new Estado(0.0, x0, 0.0, 0.0, vy0);
double t=10.0; //resolver la e. d. hasta este instante
new Planeta().resolver(t, es, h);
System.out.println("posición aprox. x "+es.x);
System.out.println("posición aprox. y "+es.y);
System.out.println("velocidad aprox. vx "+es.vx);
System.out.println("velocidad aprox. vy "+es.vy);