Sistemas de partículas

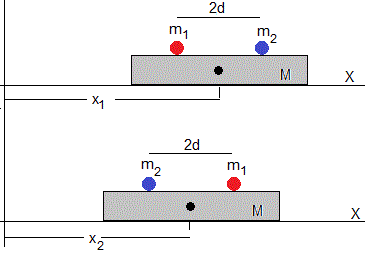
1.-Una plataforma de masa M se puede mover sin rozamiento sobre el plano horizontal. Dos partículas de masas m₁ y m₂ distan 2d tal como se muestra en la figura

Las dos partículas intercambian sus posiciones, como consecuencia la plataforma se desplaza y hacia la izquierda. Calcular la masa m₂ de la partícula

Datos: M=30 kg, m₁=80 kg, 2d=3 m, y=40 cm

Masatsugu Suzuki. Lecture Notes of General Physics I and II Calculus Based

Solución

La posición del centro de masas del sistema aislado no cambia

Sea x₁ la posición inicial del centro de la plataforma. La posición del centro de masas es

$x_{c m} = \frac{m_{1} (x_{1} - d) + M x_{1} + m_{2} (x_{1} + d)}{m_{1} + M + m_{2}} = x_{1} + \frac{m_{2} - m_{1}}{m_{1} + M + m_{2}} d$

Sea x₂ la posición final del centro de la plataforma. La posición del centro de masas es

$x_{c m} = \frac{m_{2} (x_{2} - d) + M x_{2} + m_{1} (x_{2} + d)}{m_{1} + M + m_{2}} = x_{2} + \frac{m_{1} - m_{2}}{m_{1} + M + m_{2}} d$

El centro de la plataforma se desplaza y=x₁-x₂

$y = x_{1} - x_{2} = \frac{m_{1} - m_{2}}{m_{1} + M + m_{2}} 2 d$

Con los datos del problema, m₂=57.6 kg

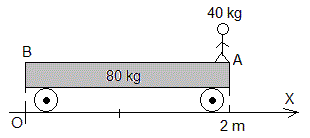
2.-Desde el extremo de una plataforma móvil de 80 kg, inicialmente en reposo, un niño de 40 kg corre hacia el otro extremo a una velocidad constante de 1 m/s (respecto de la plataforma). Determinar la velocidad de la plataforma y el sentido de su movimiento. ¿Qué principio físico aplicas?

Solución

3.-Desde el extremo A de una plataforma móvil de 80 kg inicialmente en reposo, un niño de 40 kg se desplaza hasta su extremo B. Determinar la posición del niño y del centro de la plataforma cuando el niño se encuentra en B. Razónese la respuesta.

El niño se desplaza de A a B con velocidad constante de 1 m/s sobre la plataforma. Determinar la velocidad de la plataforma y el sentido de su movimiento. Razónese la respuesta

Solución

Sistema aislado

$\begin{array}{l} \vec{F_{e x t}} = \frac{d \vec{P}}{d t} \vec{F_{e x t}} = m \frac{d \vec{V_{c}}}{d t} \\ \vec{F_{e x t}} = 0 \vec{V_{c}} = cte \end{array}$

El niño y la plataforma constituyen un sistema aislado de dos partículas, el centro de masa que está inicialmente en reposo sigue en reposo en la misma posición

$x_{c m} = \frac{80 \cdot 1 + 40 \cdot 2}{80 + 40} = \frac{4}{3} m$

Como vemos en el dibujo, la posición del niño es x_cm-(2-x_cm)=2x_cm-2=2/3 m. La posición del centro de la plataforma es x_cm +(x_cm-1)= 2x_cm-1=5/3 m

El niño y la plataforma constituyen un sistema aislado de dos partículas, el centro de masa que está inicialmente en reposo, su velocidad es cero, no se modifica. O de otra forma, el momento total inicial del sistema es cero y el momento lineal final deberá ser cero.

Si la velocidad de la plataforma es v, la velocidad del niño respecto de a Tierra es v-1.

80·v+40(v-1)=0, la velocidad de la plataforma es v=1/3 m/s

4.-Un barquero trata de cruzar un lago con un bote cargado de piedras del mismo tamaño de masa m=1 kg. El motor del bote se ha estropeado y no hay viento, ni corriente, ni dispone de remos para acercarse hasta la orilla opuesta.

El barquero empieza a lanzar secuencialmente una piedra detrás de la otra con una velocidad de u=4 m/s respecto del barco. La masa inicial del barco es M=150 kg (incluido el barquero y las n piedras).

Calcular la velocidad del bote después de lanzar la tercera piedra.

Miguel Lagos, Milton Elgueta, and Rodrigo Paredes, Mario I. Molina. Waterways and Rocket-Propulsion Problems. The Physics Teacher. Vol.61, November 2023. pp. 672-674

Solución

El barquero lanza la primera piedra

El momento lineal inicial es p=0

$\begin{array}{l} m (- u) + (M - m) v_{1} = 0 \\ v_{1} = \frac{m}{M - m} u \end{array}$

El barquero lanza la segunda piedra

El momento lineal inicial es p=(M-m)v₁

$\begin{array}{l} m (- u + v_{1}) + (M - 2 m) v_{2} = (M - m) v_{1} \\ v_{2} = v_{1} + \frac{m}{M - 2 m} u = (\frac{m}{M - m} + \frac{m}{M - 2 m}) u \end{array}$

-u+v₁ es la velocidad de la piedra respecto del lago

El barquero lanza la tercera piedra

El momento lineal inicial es p=(M-2m)v₂

$\begin{array}{l} m (- u + v_{2}) + (M - 3 m) v_{3} = (M - 2 m) v_{2} \\ v_{3} = v_{2} + \frac{m}{M - 3 m} u = (\frac{m}{M - m} + \frac{m}{M - 2 m} + \frac{m}{M - 3 m}) u \end{array}$

Sustituyendo los datos

$v_{3} = (\frac{1}{149} + \frac{1}{148} + \frac{1}{147}) 4 = 0.081 m/s$

El barquero lanza n piedras secuencialmente

La velocidad final de la barca es

$v_{n} = (\sum_{k = 1}^{n} \frac{m}{M - k m}) u$

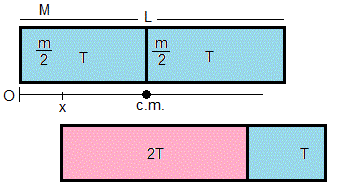
5.-Un recipiente de masa M y longitud L está en reposo. Está dividido en dos partes por un émbolo de masa despreciable que se puede mover sin rozamiento. La parte izquierda contiene una masa m/2 de gas ideal a la temperatura T. La parte derecha contiene la misma cantidad de gas y a la misma temperatura.

Se calienta la porción izquierda hasta que alcanza la temperatura 2T. La temperatura de la porción derecha permanece inalterada.

El resultado es que el recipiente se mueve x.

Physics Challenge for Teachers and Students. Think inside the box. The Physics Teacher. Vol. 55, February 2017. pp. 121

Solución

La ecuación de estado del gas ideal contenido en el recipiente izquierdo es, pV₁=nR(2T)
La ecuación de estado del gas ideal contenido en el recipiente derecho es, pV₂=nRT

Luego, la relación de volúmenes es, V₁=2V₂

Si la sección del recipiente es A

$\begin{array}{l} L_{1} = 2 L_{2} \\ L_{1} + L_{2} = L \end{array}} L_{1} = \frac{2}{3} L, L_{2} = \frac{1}{3} L$

La posición inicial del centro de masas es L/2. Como no hay fuerzas horizontales externas actuando sobre el sistema, la posición del centro de masas no cambia y como consecuencia el recipiente se mueve x. Supongamos que se mueve hacia la derecha, tal como indica la figura

$\frac{L}{2} = \frac{M (x + \frac{L}{2}) + \frac{m}{2} (x + \frac{1}{3} L) + \frac{m}{2} (x + \frac{2}{3} L + \frac{1}{6} L)}{M + \frac{m}{2} + \frac{m}{2}}$

El resultado es

$x = - \frac{1}{12} \frac{m}{m + M} L$

El recipiente se mueve x hacia la izquierda

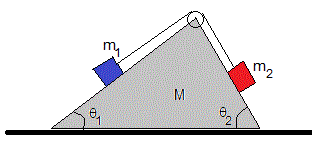
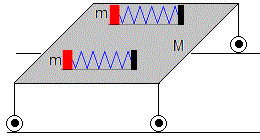
6.-Un prisma triangular de masa M se coloca sobre un plano horizontal sobre el cual puede deslizar sin rozamiento. Sobre los otros dos lados inclinados θ₁ y θ₂, se colocan dos bloques de masas m₁ y m₂, respectivamente, conectadas por un hilo inextensible que pasa por una polea de masa despreciable sujeta en el vértice. Los bloques pueden deslizar sin rozamiento a lo largo de sus respectivos planos inclinados. Calcular:

la aceleración a₀ del prisma
la aceleración a de los masas relativa al prisma
El cociente de las masas m₁/m₂ para que el prisma esté en equilibrio

Problema propuesto en la V Olimpiada Internacional de Física, Sofía, Bulgaria (1971)

Solución

Aceleraciones de los cuerpos

Las aceleraciones relativas al prisma de los bloques tienen el mismo módulo a por estar los bloques unidos mediante una cuerda inextensible.

Del prisma

La aceleración del prisma es $\vec{a_{0}}$ , paralela al plano horizontal

Del bloque de masa m₁

La aceleración del bloque de masa m₁ relativa al prisma es $\vec{a_{1}}$ su módulo es a y su dirección es paralela al plano inclinado θ₁

La aceleración de este bloque respecto al S. R. inercial es

$\vec{A_{1}} = \vec{a_{0}} + \vec{a_{1}} {\begin{cases} A_{1 x} = a_{0} + a \cos θ_{1} \\ A_{1 y} = a \sin θ_{1} \end{cases}$

Del bloque de masa m₂

La aceleración del bloque de masa m₂ relativa al prisma es $\vec{a_{2}}$ su módulo es a y su dirección es paralela al plano inclinado θ₂

La aceleración de este bloque respecto al S. R. inercial es

$\vec{A_{2}} = \vec{a_{0}} + \vec{a_{2}} {\begin{cases} A_{2 x} = a_{0} + a \cos θ_{2} \\ A_{2 y} = - a \sin θ_{2} \end{cases}$

Ecuaciones del movimiento de cada uno de los cuerpos

Bloque de masa m₁

Sobre este bloque actúa el peso m₁g, la tensión de la cuerda T₁ en la dirección del plano sobre el que desliza, la reacción del plano inclinado N₁, perpendicular a dicho plano. La ecuación del movimiento es

$m_{1} \vec{A_{1}} = m_{1} \vec{g} + \vec{T_{1}} + \vec{N_{1}} {\begin{cases} m_{1} (a_{0} + a \cos θ_{1}) = T_{1} \cos θ_{1} - N_{1} \sin θ_{1} \\ m_{1} (a \sin θ_{1}) = T_{1} \sin θ_{1} + N_{1} \cos θ_{1} - m_{1} g \end{cases}$

Bloque de masa m₂

Sobre este bloque actúa el peso m₂g, la tensión de la cuerda T₂ en la dirección del plano sobre el que desliza, la reacción del plano inclinado N₂, perpendicular a dicho plano. La ecuación del movimiento es

$m_{2} \vec{A_{2}} = m_{2} \vec{g} + \vec{T_{2}} + \vec{N_{2}} {\begin{cases} m_{2} (a_{0} + a \cos θ_{2}) = - T_{2} \cos θ_{2} + N_{2} \sin θ_{2} \\ m_{2} (- a \sin θ_{2}) = T_{2} \sin θ_{2} + N_{2} \cos θ_{2} - m_{2} g \end{cases}$

Sobre el prisma de masa M

Sobre el prisma actúa el peso Mg, la reacción del plano horizontal N, las fuerzas que ejerce la cuerda sobre la polea T₁ y T₂, y las fuerzas que ejercen los bloques sobre los planos inclinados N₁ y N₂, que por la tercera ley de Newton son fuerzas iguales y de sentido contrario a la que ejercen los planos sobre los bloques. La ecuación del movimiento es

$\begin{array}{l} M \vec{a_{0}} = M \vec{g} - \vec{N_{1}} - \vec{N_{2}} - {\vec{T}}_{1} - \vec{T_{2}} + \vec{N} \\ {\begin{cases} M a_{0} = N_{1} \sin θ_{1} - N_{2} \sin θ_{2} - T_{1} \cos θ_{1} + T_{2} \cos θ_{2} \\ 0 = - M g - N_{1} \cos θ_{1} - N_{2} \cos θ_{2} - T_{1} \sin θ_{1} - T_{2} \sin θ_{2} + N \end{cases} \end{array}$

La segunda ecuación expresa el equilibrio del prisma en la dirección perpendicular al plano

Los módulos de ${\vec{T}}_{1}$ y ${\vec{T}}_{2}$ son iguales ya que la polea tiene masa y por tanto, momento de inercia despreciable

Tenemos un sistema de cinco ecuaciones con cinco incógnitas: las aceleraciones a₀ y a, los módulos de las fuerzas T, N₁ y N₂, que vamos a resolver a continuación

${\begin{cases} m_{1} (a_{0} + a \cos θ_{1}) = T \cos θ_{1} - N_{1} \sin θ_{1} \\ m_{1} (a \sin θ_{1}) = T \sin θ_{1} + N_{1} \cos θ_{1} - m_{1} g \\ m_{2} (a_{0} + a \cos θ_{2}) = - T \cos θ_{2} + N_{2} \sin θ_{2} \\ m_{2} (- a \sin θ_{2}) = T \sin θ_{2} + N_{2} \cos θ_{2} - m_{2} g \\ M a_{0} = N_{1} \sin θ_{1} - N_{2} \sin θ_{2} - T \cos θ_{1} + T \cos θ_{2} \end{cases}$

Para resolver el sistema, tomamos la primera, tercera y quinta ecuación

${\begin{cases} m_{1} (a_{0} + a \cos θ_{1}) = T \cos θ_{1} - N_{1} \sin θ_{1} \\ m_{2} (a_{0} + a \cos θ_{2}) = - T \cos θ_{2} + N_{2} \sin θ_{2} \\ M a_{0} = N_{1} \sin θ_{1} - N_{2} \sin θ_{2} - T \cos θ_{1} + T \cos θ_{2} \end{cases}$

Despejamos Tcosθ₁ de la primera, Tcosθ₂ de la segunda y la introducimos en la tercera, obtenemos la relación entre las aceleraciones

$a = - a_{0} \frac{M + m_{1} + m_{2}}{m_{1} \cos θ_{1} + m_{2} \cos θ_{2}}$

En el sistema formado por las dos primeras ecuaciones despejamos, T y N₁

$\begin{array}{l} {\begin{cases} m_{1} (a_{0} + a \cos θ_{1}) = T \cos θ_{1} - N_{1} \sin θ_{1} \\ m_{1} (a \sin θ_{1}) = T \sin θ_{1} + N_{1} \cos θ_{1} - m_{1} g \end{cases} \\ m_{1} a_{0} \sin θ_{1} = - N_{1} + m_{1} g \cos θ_{1} \\ m_{1} (a \cos θ_{1} + a) = T - m_{1} g \sin θ_{1} \end{array}$

En el sistema formado por la tercera y cuarta ecuaciones despejamos, T y N₂

$\begin{array}{l} {\begin{cases} m_{2} (a_{0} + a \cos θ_{2}) = - T \cos θ_{2} + N_{2} \sin θ_{2} \\ m_{2} (- a \sin θ_{2}) = T \sin θ_{2} + N_{2} \cos θ_{2} - m_{2} g \end{cases} \\ m_{2} a_{0} \sin θ_{2} = N_{2} - m g \cos θ_{2} \\ m_{2} (a_{0} \cos θ_{2} + a) = - T + m_{2} g \sin θ_{2} \end{array}$

Eliminamos la tensión T en el sistema

$\begin{array}{l} {\begin{cases} m_{1} (a \cos θ_{1} + a) = T - m_{1} g \sin θ_{1} \\ m_{2} (a_{0} \cos θ_{2} + a) = - T + m_{2} g \sin θ_{2} \end{cases} \\ (m_{1} \cos θ_{1} + m_{2} \cos θ_{2}) a_{0} + (m_{1} + m_{2}) a = m_{2} g \sin θ_{2} - m_{1} g \sin θ_{1} \end{array}$

Introducimos el valor de la aceleración a en esta ecuación y despejamos a₀

$a_{0} = g \frac{(m_{2} \sin θ_{2} - m_{1} \sin θ_{1}) (m_{1} \cos θ_{1} + m_{2} \cos θ_{2})}{{(m_{1} \cos θ_{1} + m_{2} \cos θ_{2})}^{2} - (m_{1} + m_{2} + M) (m_{1} + m_{2})}$

La aceleración a₀=0, el bloque no se mueve, cuando

$\frac{m_{1}}{m_{2}} = \frac{\sin θ_{2}}{\sin θ_{1}}$

7.-Consideremos un par de cañones cuyos proyectiles tienen una masa m cada uno, son impulsadas por muelles elásticos comprimidos. Los cañones están situados sobre una plataforma de masa M que puede moverse sobre vías horizontales sin rozamiento.

La plataforma está inicialmente en reposo con los dos cañones en posición de disparo. La energía potencial almacenada por el muelle elástico deformado es E, supondremos que se convierte integramente en energía cinética del proyectil y de la plataforma

Calcular la velocidad final de la plataforma cuando los dos proyectiles se disparan

Simultáneamente
Secuencialmente, después de haber disparado el primero, se dispara el segundo

Carl E. Mungan. The Dual-Spring-Cannon-Propelled Cart. Physics Education. January – March 2020

Solución

Simultáneamente

Sistema aislado (plataforma-cañones). Conservación del momento lineal

$2 m u_{1} = M v_{1}$

Balance energético

$2 E = 2 \frac{1}{2} m u_{1}^{2} + \frac{1}{2} M v_{1}^{2}$

La energía potencial de los muelles deformados se transforma integramente en energía cinética de los proyectiles y de la plataforma. Despejando las velocidad de los proyeciles u₁ y de la plataforma v₁

$\begin{array}{l} v_{1} = \sqrt{\frac{8 m E}{M (M + 2 m)}} \\ u_{1} = \sqrt{\frac{2 M E}{m (M + 2 m)}} \end{array}$

Secuencialmente

Primer disparo

Conservación del momento lineal

$m u = (M + m) v$

Balance energético

$E = \frac{1}{2} m u^{2} + \frac{1}{2} (M + m) v^{2}$

Despejamos la velocidad de la plataforma v y del proyectil u

$\begin{array}{l} v = \sqrt{\frac{2 E m}{(M + m) (M + 2 m)}} \\ u = \sqrt{\frac{2 E (M + m)}{m (M + 2 m)}} \end{array}$

Segundo disparo

Una vez completado el primer disparo, procedemos a realizar el segundo

Nos situamos en el sistema de referencia que se mueve con la plataforma

Conservación del momento lineal

$m U = M V$

Balance energético

$E = \frac{1}{2} m U^{2} + \frac{1}{2} M V^{2}$

Despejamos la velocidad de la plataforma V y del proyectil U

$\begin{array}{l} V = \sqrt{\frac{2 E m}{M (M + m)}} \\ U = \sqrt{\frac{2 E M}{m (M + m)}} \end{array}$

En el sistema de referencia ligado al suelo

$\begin{array}{l} v_{2} = V + v = \sqrt{\frac{2 E m}{M (M + m)}} + \sqrt{\frac{2 E m}{(M + m) (M + 2 m)}} \\ u_{2} = - U + v = - \sqrt{\frac{2 E M}{m (M + m)}} + \sqrt{\frac{2 E m}{(M + m) (M + 2 m)}} \end{array}$

Representamos gráficamente el cociente v₂/v₁ en función del cociente M/m

$\frac{v_{2}}{v_{1}} = \frac{\sqrt{M + 2 m} + \sqrt{M}}{2 \sqrt{M + m}} = \frac{\sqrt{r + 2} + \sqrt{r}}{2 \sqrt{r + 1}}, r = \frac{M}{m}$

Cuando m<<M, el cociente tiende hacia 1

f=@(x) (sqrt(x)+sqrt(x+2))./(2*sqrt(x+1));
fplot(f,[1,5])
grid on
xlabel('M/m')
ylabel('v_2/v_1')
title('Simultáneo o secuencial')

La plataforma alcanza una velocidad mayor, si los dos disparos se producen de forma simultánea

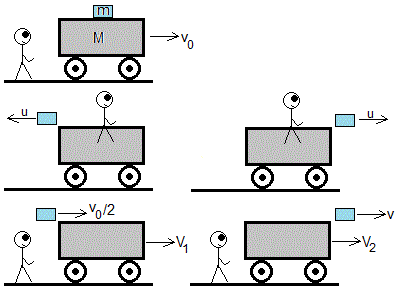
8.-Una caja de masa m descansa sobre una plataforma de masa M que se mueve velocidad constante v₀

Si se arroja la caja desde la plataforma con velocidad u (respecto de la plataforma) hacia atrás, el observador en Tierra mide que su velocidad es v₀/2, y la velocidad de la plataforma es V₁
Si se arroja la caja desde la plataforma con velocidad u (respecto de la plataforma) hacia adelante, el observador en Tierra mide que su velocidad es v y la velocidad de la plataforma es V₂

Dado las masas m y M y la velocidad v₀, determinar la velocidad de la caja v, las velocidades de la plataforma V₁ y V₂ respecto del observador en Tierra y la velocidad u de la caja respecto del observador en la plataforma.

Despreciamos la resistencia del aire y el rozamiento entre la plataforma y el suelo

Kirk T. McDonald. Box Toss. October 2011

Solución

Tenemos un sistema aislado, formado por la caja y la plataforma, la conservación del momento lineal para cada uno de los dos casos, se escribe

$\begin{array}{l} (M + m) v_{0} = m \frac{v_{0}}{2} + M V_{1} \\ (M + m) v_{0} = m v + M V_{2} \end{array}$

Relación entre velocidades

$\begin{array}{l} - u = \frac{v_{0}}{2} - V_{1} \\ u = v - V_{2} \end{array}$

Resolvemos el sistema de ecuaciones (se puede hacer de varias maneras)

De las dos últimas, eliminamos u

$v = V_{1} + V_{2} - \frac{v_{0}}{2}$

De la primera, despejamos V₁

$V_{1} = (\frac{m}{2 M} + 1) v_{0}$

En la segunda, introducimos v y V₁ y despejamos V₂

$\begin{array}{l} (\frac{m}{2} + M - \frac{m^{2}}{2 M}) v_{0} = (m + M) V_{2} \\ V_{2} = \frac{1}{m + M} \frac{m M + 2 M^{2} - m^{2}}{2 M} v_{0} = \frac{2 M - m}{2 M} v_{0} \end{array}$

Dado V₁ y V₂ calculamos la velocidad v de la caja

$v = \frac{3}{2} v_{0}$

Dado v y V₂, calculamos la velocidad relativa u de la caja respecto de la plataforma

$u = \frac{1}{2} (1 + \frac{m}{M}) v_{0}$

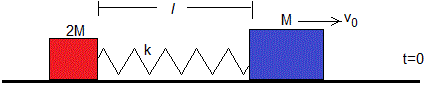
9.-Dos cuerpos de masa 2M y M están unidos por un muelle elástico de constante k y longitud l sin deformar, los cuerpos están en reposo sobre una superficie horizontal sin rozamiento.

En el instante t=0, se proporciona al cuerpo de masa M una velocidad v₀ que lo aleja del otro cuerpo

Determinar el desplazamiento del cuerpo de masa M la próxima vez que vuelva a alcanza la velocidad v₀

Physics Challenge for Teachers and Students. January jiggle. Phys. Teach. 58, 70 (2020)

Solución

En el instante t=0 el cuerpo de masa 2M está en el origen en reposo. El cuerpo de masa M está a una distancia l con velocidad inicial v₀

En el instante t, la posición del cuerpo de masa 2M es x y su velocidad es V=dx/dt, la posición del cuerpo de masa M es y y su velocidad es v=dy/dt.

Movimiento del centro de masas

En un sistema aislado de dos partículas interactuantes, el centro de masas se mueve con velocidad constante

La posición inicial y la velocidad del centro de masas, t=0

$z_{0} = \frac{M l}{M + 2 M} = \frac{l}{3}, v_{c m} = \frac{0 + M v_{0}}{M + 2 M} = \frac{v_{0}}{3}$

En el instante t

$\begin{array}{l} z = \frac{l}{3} + \frac{v_{0}}{3} t \\ z = \frac{2 M x + M y}{M + 2 M} = \frac{2 x + y}{3} \\ 2 x + y = l + v_{0} t \end{array}$

Movimiento relativo de las dos partículas

En el instante t, el muelle se ha deformado (y-x-l) y ejerce fuerzas F=k(y-x-l) iguales y de sentido contario sobre cada una de las partículas. Las ecuaciones del movimiento son

$\begin{array}{l} 2 M \frac{d^{2} x}{d t^{2}} = k (y - x - l) \\ M \frac{d^{2} y}{d t^{2}} = - k (y - x - l) \end{array}$

Multiplicamos la segunda ecuación por 2 y restamos la segunda de la primera.

$\begin{array}{l} 2 M (\frac{d^{2} y}{d t^{2}} - \frac{d^{2} x}{d t^{2}}) = - 3 k (y - x - l) \\ 2 M \frac{d^{2} ξ}{d t^{2}} = - 3 k (ξ - l), ξ = y - x \\ \frac{d^{2} ξ}{d t^{2}} + \frac{3 k}{2 M} ξ = \frac{3 k}{2 M} l \end{array}$

donde ξ=y-x es la posición relativa de las dos partículas.

La solución de esta ecuación diferencial se compone de la suma de solución de la ecuación dierencial homogénea y de un término constante l

$\begin{array}{l} ξ = l + A \sin (ω t) + B \cos (ω t), ω = \sqrt{\frac{3 k}{2 M}} \\ \frac{d ξ}{d t} = A ω \cos (ω t) - B ω \sin (ω t) \end{array}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales.

$\begin{array}{l} t = 0 {\begin{cases} x = 0, y = l \\ \frac{d x}{d t} = 0, \frac{d y}{d t} = v_{0} \end{cases} \\ t = 0 {\begin{cases} ξ = l \\ \frac{d ξ}{d t} = v_{0} \end{cases} \end{array}$

El resultado es

$B = 0, A = \frac{v_{0}}{ω}$

La posición relativa ξ es

$ξ = l + \frac{v_{0}}{ω} \sin (ω t)$

Conocemos la posición del c.m. y la posición relativa de los cuerpos en función del tiempo t. Despejamos la posición x e y de cada uno de los cuerpos

$\begin{array}{l} {\begin{cases} 2 x + y = l + v_{0} t \\ y - x = l + \frac{v_{0}}{ω} \sin (ω t) \end{cases} \\ {\begin{cases} x = \frac{1}{3} v_{0} t - \frac{1}{3} \frac{v_{0}}{ω} \sin (ω t) \\ y = l + \frac{1}{3} v_{0} t + \frac{2}{3} \frac{v_{0}}{ω} \sin (ω t) \end{cases} \end{array}$

v0=1; %velocidad inicial
l=1; %longitud del muelle sin deformar
k=1; %constante del muelle
M=1; %masa
w=sqrt(3*k/(2*M)); %frecuencia angular
x=@(t) v0*t/3-v0*sin(w*t)/(3*w);
y=@(t) l+v0*t/3+2*v0*sin(w*t)/(3*w);
hold on
fplot(x,[0,2*pi/w])
fplot(y,[0,2*pi/w])
hold off
grid on
xlabel('t (s)')
ylabel('x,y (m)')
legend('2M','M','location', 'best')
title('Posición')

Derivando con respecto del tiempo t, obtenemos la velocidad de los cuerpos

$\begin{array}{l} {\begin{cases} \frac{d x}{d t} = \frac{1}{3} v_{0} - \frac{1}{3} v_{0} \cos (ω t) \\ \frac{d y}{d t} = \frac{1}{3} v_{0} + \frac{2}{3} v_{0} \cos (ω t) \end{cases} \\ v_{c m} = \frac{2 M \frac{d x}{d t} + M \frac{d y}{d t}}{2 M + M} = \frac{v_{0}}{3} \end{array}$

Comprobamos que la velocidad constante del centro de masas del sistema aislado es v₀/3

v0=1; %velocidad inicial
k=1; %constante del muelle
M=1; %masa
w=sqrt(3*k/(2*M)); %frecuencia angular
vx=@(t) v0/3-v0*cos(w*t)/3;
vy=@(t) v0/3+2*v0*cos(w*t)/3;
hold on
fplot(vx,[0,2*pi/w])
fplot(vy,[0,2*pi/w])
hold off
grid on
xlabel('t (s)')
ylabel('v_x,v_y (m)')
legend('2M','M','location', 'best')
title('Velocidad')

En el instante ωt=2π, dy/dt=v₀.

Calculamos el desplazamiento Δy del cuerpo de masa M

$\begin{array}{l} y = l + \frac{v_{0}}{3} \frac{2 π}{ω} \\ Δ y = \frac{2 π v_{0}}{3} \sqrt{\frac{2 M}{3 k}} \end{array}$

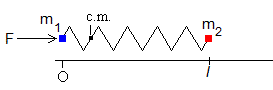
10.-Sean dos partículas de masas m₁ y m₂ respectivamente, unidas por un muelle elástico de constante k y de longitud l sin deformar.

En la situación inicial la partícula de masa m₁ está en el origen x₁=0, y la partícula de masa m₂ en x₂=l, ambas en reposo. Se aplica una fuerza constante F a la primera partícula.

Escribir las ecuaciones del movimiento de cada una de las partículas
Escribir la ecuación del movimiento del centro de masas y determinar la posición x_cm(t) del centro de masas en función del tiempo
Escribir la ecuación del movimiento relativo ξ=x₂-x₁ de las dos partículas y determinar la posición relativa en función del tiempo ξ(t)
Utilizando ambas ecuaciones, determinar la ecuación del movimiento de la primera partícula x₁(t) y de la segunda, x₂(t)
Comprobar que el trabajo de la fuerza F, F·x₁, se emplea en modificar la energía del sistema de partículas.

Datos: m₁=1 kg, m₂=1 kg, k=100 N/m, l=0.25 m, F=10 N

Solución

Ecuaciones del movimiento de las dos partículas

${\begin{cases} m_{1} \frac{d^{2} x_{1}}{d t^{2}} = F + k (x_{2} - x_{1} - l) \\ m_{2} \frac{d^{2} x_{2}}{d t^{2}} = - k (x_{2} - x_{1} - l) \end{cases}$

Movimiento del centro de masas

La posición del centro de masas es

$x_{c m} = \frac{m_{1} x_{1} + m_{2} x_{2}}{m_{1} + m_{2}}$

Sumamos las dos ecuaciones diferenciales

$\begin{array}{l} m_{1} \frac{d^{2} x_{1}}{d t^{2}} + m_{2} \frac{d^{2} x_{2}}{d t^{2}} = F \\ \frac{d^{2} x_{c m}}{d t^{2}} = \frac{F}{m_{1} + m_{2}} \end{array}$

El movimiento del centro de masas solamente depende de la fuerza externa F. El centro de masas se mueve con aceleración constante, la ecuación del movimiento del c.m. es muy sencilla

$x_{c m} = \frac{m_{2} l}{m_{1} + m_{2}} + \frac{1}{2} \frac{F}{m_{1} + m_{2}} t^{2}$

El primer término, es la posición inicial del centro de masas. El centro de masas parte del reposo, al igual que las dos partículas

Movimiento relativo de las partículas, ξ=x₂-x₁

$\begin{array}{l} {\begin{cases} \frac{d^{2} x_{1}}{d t^{2}} = \frac{F}{m_{1}} + \frac{k}{m_{1}} (x_{2} - x_{1} - l) \\ \frac{d^{2} x_{2}}{d t^{2}} = - \frac{k}{m_{2}} (x_{2} - x_{1} - l) \end{cases} \\ \frac{d^{2} (x_{2} - x_{1})}{d t^{2}} = - \frac{F}{m_{1}} - \frac{k}{m_{1}} (x_{2} - x_{1} - l) - \frac{k}{m_{2}} (x_{2} - x_{1} - l) \\ \frac{d^{2} ξ}{d t^{2}} = - \frac{F}{m_{1}} - \frac{k}{μ} (ξ - l), μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}} \end{array}$

μ se denomina masa reducida

Buscamos la solución de la ecuación diferencial

$\frac{d^{2} ξ}{d t^{2}} + \frac{k}{μ} ξ = - \frac{F}{m_{1}} + \frac{k}{μ} l$

La solución particular es una constante ξ_p

$\begin{array}{l} \frac{k}{μ} ξ_{p} = - \frac{F}{m_{1}} + \frac{k}{μ} l \\ ξ_{p} = l - \frac{F}{m_{1}} \frac{μ}{k} \end{array}$

La solución de la ecuación homogénea ξ_h, es

$ξ_{h} = A \sin (ω t) + B \cos (ω t), ω^{2} = \frac{k}{μ}$

La solución completa es la suma

$ξ = ξ_{h} + ξ_{p} = A \sin (ω t) + B \cos (ω t) + l - \frac{F}{m_{1}} \frac{μ}{k}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales, en el instante t=0, ξ=x₂-x₁=l, parten del reposo dξ/dt=0

$\begin{array}{l} l = B + l - \frac{F}{m_{1}} \frac{μ}{k}, B = \frac{F}{m_{1}} \frac{μ}{k} \\ \frac{d ξ}{d t} = ω A \cos (ω t) - ω B \sin (ω t) \\ {\frac{d ξ}{d t} |}_{t = 0} = ω A = 0, A = 0 \end{array}$

La solución de la ecuación diferencial del movimiento relativo es

$ξ = \frac{F}{m_{1}} \frac{μ}{k} \cos (ω t) + l - \frac{F}{m_{1}} \frac{μ}{k} = l - 2 \frac{F}{m_{1}} \frac{μ}{k} \sin^{2} (\frac{ω t}{2})$

Del sistema de dos ecuaciones (movimiento del c.m. y movimiento relativo), despejamos x₁ y x₂ en función del tiempo

$\begin{array}{l} {\begin{cases} \frac{m_{1} x_{1} + m_{2} x_{2}}{m_{1} + m_{2}} = \frac{m_{2} l}{m_{1} + m_{2}} + \frac{1}{2} \frac{F}{m_{1} + m_{2}} t^{2} \\ x_{2} - x_{1} = l - 2 \frac{F}{m_{1}} \frac{μ}{k} \sin^{2} (\frac{ω t}{2}) \end{cases} \\ x_{1} = \frac{1}{2} \frac{F}{m_{1} + m_{2}} t^{2} + 2 \frac{μ}{k} \frac{m_{2}}{m_{1}} \frac{F}{m_{1} + m_{2}} \sin^{2} (\frac{ω t}{2}) \\ x_{2} = l + \frac{1}{2} \frac{F}{m_{1} + m_{2}} t^{2} - 2 \frac{μ}{k} \frac{F}{m_{1} + m_{2}} \sin^{2} (\frac{ω t}{2}) \end{array}$

El trabajo de la fuerza F igual a la variación de la energía del sistema de partículas

El trabajo de la fuerza exterior F es

$F \cdot x_{1} = \frac{1}{2} \frac{F^{2}}{m_{1} + m_{2}} t^{2} + 2 \frac{μ}{k} \frac{m_{2}}{m_{1}} \frac{F^{2}}{m_{1} + m_{2}} \sin^{2} (\frac{ω t}{2})$

La energía del sistema de partículas es la suma de la energía cinética de las dos partículas y de la energía potencial de interacción de las dos partículas

La energía inicial del sistema de partículas U_i=0 en el instante t=0

La energía cinética de las dos partículas en el instante t

$\begin{array}{l} E_{k 1} = \frac{1}{2} m_{1} {(\frac{d x_{1}}{d t})}^{2} = \frac{1}{2} m_{1} {(\frac{F}{m_{1} + m_{2}} t + 2 ω \frac{μ}{k} \frac{m_{2}}{m_{1}} \frac{F}{m_{1} + m_{2}} \sin (\frac{ω t}{2}) \cos (\frac{ω t}{2}))}^{2} \\ E_{k 2} = \frac{1}{2} m_{2} {(\frac{d x_{2}}{d t})}^{2} = \frac{1}{2} m_{2} {(\frac{F}{m_{1} + m_{2}} t - 2 ω \frac{μ}{k} \frac{F}{m_{1} + m_{2}} \sin (\frac{ω t}{2}) \cos (\frac{ω t}{2}))}^{2} \\ E_{k 1} + E_{k 2} = \frac{1}{2} \frac{F^{2}}{m_{1} + m_{2}} t^{2} + 2 \frac{μ}{k} \frac{F^{2}}{m_{1} + m_{2}} \frac{m_{2}}{m_{1}} \sin^{2} (\frac{ω t}{2}) \cos^{2} (\frac{ω t}{2}) \end{array}$

La energía potencial de interacción del sistema de dos partículas

$E_{p 12} = \frac{1}{2} k {(x_{2} - x_{1} - l)}^{2} = \frac{1}{2} k {(- 2 \frac{μ}{k} \frac{F}{m_{1}} \sin^{2} (\frac{ω t}{2}))}^{2} = 2 \frac{μ}{k} \frac{F^{2}}{m_{1} + m_{2}} \frac{m_{2}}{m_{1}} \sin^{4} (\frac{ω t}{2})$

La suma

$U_{f} = E_{k 1} + E_{k 2} + E_{p 12} = \frac{1}{2} \frac{F^{2}}{m_{1} + m_{2}} t^{2} + 2 \frac{μ}{k} \frac{m_{2}}{m_{1}} \frac{F^{2}}{m_{1} + m_{2}} \sin^{2} (\frac{ω t}{2})$

Confirmamos que el trabajo de la fuerza exterior F se invierte en modificar la energía del sistema de partículas

Representamos las posiciones de las dos partículas x₁(t), x₂(t) y la posición del centro de masas x_cm(t)

k=100;    %constante elástica del muelle
m1=1;  %masa izquierda
m2=4; %masa derecha
F=10; %fuerza externa
lonMuelle=0.25; %longitud del muelle sin deformar
mu=m1*m2/(m1+m2); %masa reducida
w=sqrt(k/mu); %frecuencia angular
x1=@(t) F*t.^2/(2*(m1+m2))+2*mu*m2*F*sin(w*t/2).^2/(k*m1*(m1+m2));
x2=@(t) lonMuelle+F*t.^2/(2*(m1+m2))-2*mu*F*sin(w*t/2).^2/(k*(m1+m2));
xcm=@(t) m2*lonMuelle/(m1+m2)+F*t.^2/(2*(m1+m2));
hold on
fplot(x1,[0,1])
fplot(x2,[0,1])
fplot(xcm,[0,1])
hold off
grid on
legend('x_1','x_2','x_{cm}','Location', 'best')
xlabel('t(s)')
ylabel('x')
title('Sistema de dos partículas')

Representamos la energía cinética de cada una de las partículas E_k1(t), E_k2(t), la energía potencial de interación E_p(t) y el trabajo de la fuerza externa, F·x₁(t),

k=100;    %constante elástica del muelle
m1=1;  %masa izquierda
m2=4; %masa derecha
F=10; %fuerza externa
lonMuelle=0.25; %longitud del muelle sin deformar
mu=m1*m2/(m1+m2); %masa reducida
w=sqrt(k/mu); %frecuencia angular
x1=@(t) F*t.^2/(2*(m1+m2))+2*mu*m2*F*sin(w*t/2).^2/(k*m1*(m1+m2));
x2=@(t) lonMuelle+F*t.^2/(2*(m1+m2))-2*mu*F*sin(w*t/2).^2/(k*(m1+m2));
v1=@(t) F*t/(m1+m2)+w*mu*m2*F*sin(w*t)/(k*m1*(m1+m2));
v2=@(t) F*t/(m1+m2)-w*mu*F*sin(w*t)/(k*(m1+m2));
Ek_1=@(t) m1*v1(t).^2/2;
Ek_2=@(t) m2*v2(t).^2/2;
Ep=@(t) k*(x2(t)-x1(t)-lonMuelle).^2/2;
U=@(t) Ek_1(t)+Ek_2(t)+Ep(t);
W=@(t) F*x1(t);

hold on
fplot(Ek_1,[0,1])
fplot(Ek_2,[0,1])
fplot(Ep,[0,1])
% fplot(U,[0,1])
fplot(W,[0,1])
hold off
grid on
legend('E_{k1}','E_{k2}','E_p', 'W', 'Location', 'best')
xlabel('t(s)')
ylabel('Energía')
title('Sistema de dos partículas')