Una máquina de Atwood gigantesca

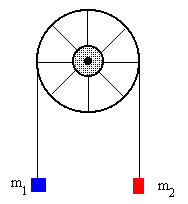La máquina de Atwood es un clásico ejemplo de la aplicación de la segunda ley de Newton. Consta de una polea fija y una cuerda inextensible y de masa despreciable que pasa por la polea y de cuyos extremos cuelgan dos masas.

Primero, se considera que la polea tiene un momento de inercia despreciable y cuando se estudia la dinámica de rotación, se proporciona el dato del momento de inercia de la polea.

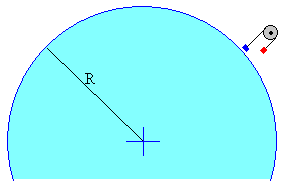En esta página, se estudia el movimiento de una máquina de Atwood gigantesca. Consta de una rueda que supondremos de masa despreciable, situada a altura grande sobre el suelo. Por la rueda pasa una cuerda inextensible y de masa despreciable del cual cuelgan dos masas iguales. Estudiaremos el efecto de la variación de la aceleración de la gravedad con la altura sobre el movimiento de los cuerpos.

La máquina de Atwood

En la figura, se muestran las fuerzas sobre cada uno de los dos cuerpos, supondremos que m₁>m₂. Consideramos que la aceleración de la gravedad g es constante en módulo y dirección

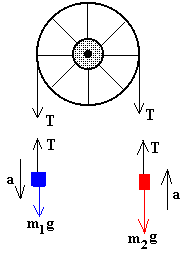Aplicamos la segunda ley de Newton a cada uno de los cuerpos

m₁g-T=m₁a
T-m₂g=m₂a

Despejamos la aceleración

$a = \frac{m_{1} - m_{2}}{m_{1} + m_{2}} g$

La velocidad de los cuerpos cuando el primero desciende una altura h partiendo del reposo es

$v = \sqrt{2 a h} = \sqrt{2 \frac{m_{1} - m_{2}}{m_{1} + m_{2}} g h}$

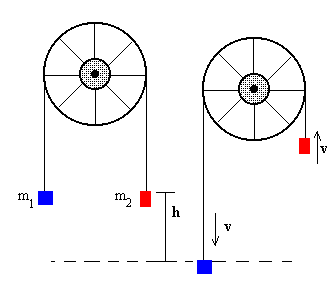
Aplicando el principio de conservación de la energía, se llega al mismo resultado. Comparamos el estado inicial y el estado final cuando el cuerpo de masa m₁ desciende una altura h, y el cuerpo de masa m₂ asciende la misma altura. Ponemos el nivel cero de energía potencial en la posición inicial de los dos cuerpos. Igualamos la energía inicial y la energía final.

$0 = - m_{1} g h + m_{2} g h + \frac{1}{2} m_{1} v^{2} + \frac{1}{2} m_{2} v^{2}$

Una máquina de Atwood gigantesca

Si los dos cuerpos tienen la misma masa y están a la misma altura, la máquina de Atwood estará en equilibrio inestable. En cambio, si los dos cuerpos están inicialmente a distinta altura la variación de la aceleración de la gravedad con la altura hace que el cuerpo más cercano a la Tierra experimente una fuerza mayor que el cuerpo más alejado.

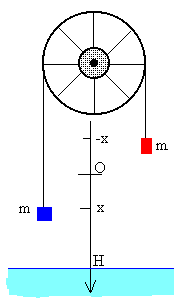Establecemos el origen en la posición de equilibrio de los dos cuerpos, cuando están a la misma altura H sobre la superficie de la Tierra. Se desplazan una distancia x los dos cuerpos, uno hacia arriba y otro hacia abajo. La fuerza que experimenta el cuerpo más cercano al suelo es

$F_{1} = G \frac{M m}{{(R + H - x)}^{2}}$

y el más alejado

$F_{2} = G \frac{M m}{{(R + H + x)}^{2}}$

Siendo R=6.37·10⁶ m el radio de la Tierra, M=5.98·10²⁴ kg la masa de la Tierra, G=6.67·10^-11 Nm²/kg², y m es la masa de cada uno de los dos cuerpos.

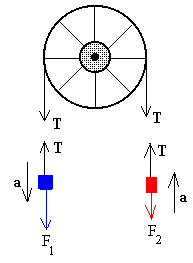Aplicamos la segunda ley de Newton a cada uno de los dos cuerpos

F₁-T=ma
T-F₂=ma

Despejamos la aceleración

a=(F₁-F₂)/(2m)

Teniendo en cuenta que H y x son muy pequeños frente al radio R de la Tierra, podemos obtener una expresión sencilla de la aceleración a en función del desplazamiento x.

$F_{1} - F_{2} = G \frac{M m}{R^{2}} {{(1 + \frac{H - x}{R})}^{- 2} - {(1 + \frac{H + x}{R})}^{- 2}} \approx m g {(1 - 2 \frac{H - x}{R}) - (1 - 2 \frac{H + x}{R})} = m g \frac{4 x}{R}$

Escribimos la ecuación del movimiento en forma de ecuación diferencial

$\frac{d^{2} x}{d t^{2}} - \frac{2 g}{R} x = 0$

La solución de esta ecuación diferencial tiene la forma

$x = A e^{k t} + B e^{- k t} k = \sqrt{\frac{2 g}{R}}$

La velocidad de los cuerpos es

$v = \frac{d x}{d t} = k (A e^{k t} - B e^{- k t})$

Los coeficientes A y B se determinan a partir de las condiciones iniciales, en el instante t=0, el desplazamiento inicial es x=x₀, y la velocidad inicial v=0. Las expresiones de la posición y velocidad de los cuerpos son

$\begin{array}{l} x = \frac{x_{0}}{2} (e^{k t} + e^{- k t}) = x_{0} \cdot \cosh (k t) \\ v = x_{0} \cdot k \cdot sinh (k t) \end{array}$

Tiempo que tarda uno de los cuerpos en llegar al suelo.

El cuerpo más cercano a la Tierra parte de la posición x=x₀ en el instante t=0, y llega a la posición x=H en el instante t.

Despejamos el tiempo t en la ecuación H=x₀·cosh(kt)

$\begin{array}{l} H = \frac{x_{0}}{2} (e^{k t} + e^{- k t}) \\ e^{2 k t} - \frac{2 H}{x_{0}} e^{k t} + 1 = 0 \end{array}$

Haciendo el cambio de variable z=e^kt, tenemos una ecuación de segundo grado en z. La raíz que da un tiempo t positivo es

$\begin{array}{l} z = \frac{H}{x_{0}} + \sqrt{\frac{H^{2}}{x_{0}^{2}} - 1} \\ t = \sqrt{\frac{R}{2 g}} \ln (\frac{H}{x_{0}} + \sqrt{\frac{H^{2}}{x_{0}^{2}} - 1}) \end{array}$

Como podemos apreciar el tiempo t depende del cociente H/x₀. Se obtiene el mismo tiempo cuando H=100 y x₀=10, que cuando H=10 y x₀=1. Siempre que se cumpla que H<<R

Balance energético

Comparamos la situación inicial con la situación en el instante t (véase la segunda figura). Aplicamos el principio de conservación de la energía

$- G \frac{M m}{R + H - x_{0}} - G \frac{M m}{R + H + x_{0}} = \frac{1}{2} 2 m v^{2} - G \frac{M m}{R + H - x} - G \frac{M m}{R + H + x}$

Dado el desplazamiento x calculamos la velocidad v de los cuerpos

Ejemplo

La posición de equilibrio de los dos cuerpos a la misma altura H=100 m. Se desplaza los dos cuerpos x₀=10 m. Calcular el tiempo que emplea en llegar al suelo y la velocidad final de los bloques. Datos:

Radio de la Tierra, R=6.37·10⁶ m,
Masa de la Tierra M=5.98·10²⁴ kg,
Constante G=6.67·10^-11 Nm²/kg²,
Aceleración de la gravedad en la superficie de la Tierra g=GM/R²=9.83 m/s²

$\begin{array}{l} = \sqrt{\frac{6.37 \cdot 10^{6}}{2 \cdot 9.83}} \ln (\frac{100}{10} + \sqrt{\frac{100^{2}}{10^{2}} - 1}) = 1703.8 s \\ v = 10· \sqrt{\frac{2 \cdot 9.83}{6.37 \cdot 10^{6}}} senh (\sqrt{\frac{2 \cdot 9.83}{6.37 \cdot 10^{6}}} \cdot 1703.8) = 0.174801 m/s \end{array}$

Aplicando el principio de conservación de la energía

$6.67 \cdot 10^{- 11} \cdot 5.98 \cdot 10^{24} (\frac{1}{6.37 \cdot 10^{6}} + \frac{1}{6.37 \cdot 10^{6} + 200} - \frac{1}{6.37 \cdot 10^{6} + 90} - \frac{1}{6.37 \cdot 10^{6} + 110}) = \frac{1}{2} 2 v^{2}$

v=0.174795 m/s

Es muy pequeña la discrepancia entre el cálculo exacto de la velocidad y el aproximado teniendo en cuenta que H y x₀ son pequeños frente al radio R de la Tierra

Actividades

Se introduce

El desplazamiento inicial x₀, actuando en la barra de desplazamiento titulada Desplazamiento inicial.
Se ha fijado la altura inicial de equilibrio de los dos cuerpos en H=100 m

Se pulsa el botón titulado Empieza

Referencias

West J. O., The Atwood machine: two special cases. The Physics Teacher Vol. 37, February 1999, pp. 83-85