Medida de la viscosidad de un fluido con la máquina de Atwood

En esta página, se utiliza la máquina de Atwood medir la viscosidad de un fluido a diferentes temperaturas.

La máquina de Atwood

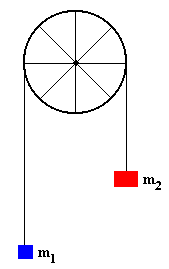La máquina de Atwood es un clásico ejemplo de la aplicación de la segunda ley de Newton. Como vemos en la figura, consta de dos cuerpos de masas m₁ y m₂ unidos por una cuerda que pasa por una polea. En la versión más simplificada, se supone que la cuerda es inextensible y sin peso, y que la polea tiene masa despreciable y gira sin rozamiento en el eje.

En la página titulada “Dinámica de rotación y balance energético”, se estudia la máquina de Atwood teniendo en cuenta la masa de la polea.

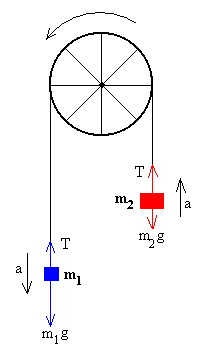En esta figura, se representan las fuerzas que actúan sobre cada una de las masas, y la aceleración a, suponiendo que m₁>m₂. Si T es la tensión de la cuerda, la segunda ley de Newton para cada una de las dos cuerpos se escribe

m₁a=m₁g-T
m₂a=T-m₂g

En este sistema dos ecuaciones, despejamos la aceleración a

$a = \frac{m_{1} - m_{2}}{m_{1} + m_{2}} g$

Medida de la viscosidad de un fluido

El cuerpo de masa m₁ es una pequeña esfera de radio R que cae en el seno de un fluido de densidad ρ, cuya viscosidad η deseamos determinar.

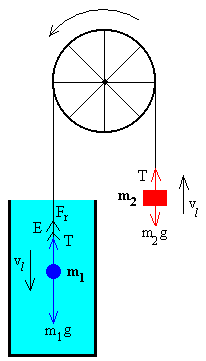Las fuerzas que actúan sobre m₁ son:

El peso m₁g
La tensión de la cuerda T
La fuerza de empuje E, que por el principio de Arquímedes vale

$E = ρ \frac{4}{3} π R^{3} g$

La fuerza de rozamiento F_r. Según la ley de Stokes vale F_r=6πR·η·v, siempre que el número de Reynolds sea menor que la unidad, Re<1

Cuando la masa m₁ cae, alcanza rápidamente una velocidad límite constante Midiendo con un cronómetro el tiempo t, que tarda la esfera en descender una altura x, obtenemos la velocidad límite v_l=x/t. Conocida la velocidad límite calculamos la viscosidad η del fluido.

Cuando la velocidad es constante o la aceleración es cero, las ecuaciones del movimiento de los dos cuerpos se escriben

m₁g-T-E-F_r=0
T-m₂g=0

Despejamos la velocidad límite v_l de fuerza de rozamiento F_r.

$v_{l} = \frac{F_{r}}{6 π R η} = (m_{1} - m_{2} - ρ \frac{4}{3} π R^{3}) \frac{g}{6 π R η}$

En la experiencia, vamos cambiando la masa m₂ y medimos la velocidad límite v_l. Si representamos v_l en función de m₂ obtendremos un conjunto de puntos que se situarán próximos a la recta

$v_{l} = (m_{1} - ρ \frac{4}{3} π R^{3}) \frac{g}{6 π R η} - \frac{g}{6 π R η} m_{2}$

cuya pendiente es

$pendiente = - \frac{g}{6 π R η}$

Cuando la masa m₂ supera un valor límite, la esfera asciende en vez de descender. El valor de m₂ para el cual la velocidad límite v_l es cero es

$m_{2} = m_{1} - ρ \frac{4}{3} π R^{3}$

Variación de la viscosidad con la temperatura

La viscosidad disminuye muy rápidamente a medida que se incrementa la temperatura. La relación entre las dos magnitudes viene dada por la fórmula empírica

$η = a \exp (\frac{b}{T})$

donde T es la temperatura en kelvin, y a y b son dos parámetros que dependen del tipo de líquido. Para la glicerina se ha tomado a=4.289·10^-12, b=7786.1. Para T=20ºC=293 K la viscosidad es

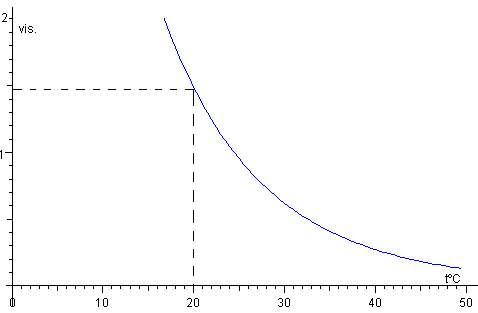
$η = 4.289 \cdot 10^{- 12} \exp (\frac{7786.1}{293}) = 1.49 kg/(m·s)$

La figura muestra la representación gráfica de esta función, en el eje horizontal la temperatura se expresa en grados Celsius.

Actividades

Se introduce

La temperatura T (en grados centígrados), actuando sobre la barra de desplazamiento titulada Temperatura.
La masa m₂ (en gramos), actuando sobre la barra de desplazamiento titulada Masa.
El radio de la esfera se ha fijado en el valor R=1.1 cm
La masa de la esfera se ha fijado en el valor m₁=15 g.
El fluido es glicerina cuya densidad es ρ=1.26 g/cm³

Se pulsa el botón titulado Empieza.

La esfera se mueve con velocidad constante. Para que la esfera descienda tenemos que poner una masa m₂ inferior a

$m_{2} = m_{1} - ρ \frac{4}{3} π R^{3} = 0.015 - 1260 \frac{4}{3} π {0.011}^{3} = 0.008 kg = 8 g$

Cuando la esfera pasa por la marca situada a la altura x=0, se pone en marcha el cronómetro, pulsando el botón titulado En marcha.
Cuando la esfera pasa por la segunda marca situada en x=40 cm, se pulsa el mismo botón titulado Parar.

Los pares de datos: masa m₂ y tiempo t que tarda la esfera en descender x=40 cm se guardan en el control área de texto situado a la izquierda del applet.

Se cambia la masa m₂, sin modificar la temperatura, y se mide el tiempo t que tarda la esfera en descender 40 cm, y se calcula la velocidad límite v_l=40/t

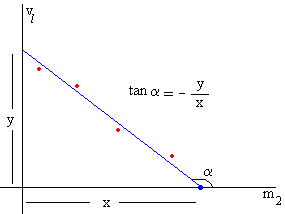Después de repetir el procedimiento varias veces con la misma temperatura, se pulsa en el botón titulado Gráfica, para representar los resultados “experimentales” y la recta que “mejor ajusta” a dichos datos. Se calcula la viscosidad a partir de la medida de la pendiente de la recta.

Ejemplo:

Para la temperatura T=20ºC, la pendiente de la recta es el cociente entre el cateto opuesto y=16 cm/s y el cateto contiguo x=8-3=5 g. La masa del cuerpo m₂ empieza en 3 g.

$pendiente = - \frac{0.16}{0.005} = 32$

En la parte superior derecha de la gráfica, el programa interactivo nos proporciona este dato con mayor precisión -31.72.

$- 31.72 = - \frac{9.8}{6 π 0.011 η} η = 1.49 kg/(m·s)$

El programa interactivo, genera el dato de la viscosidad en función de la temperatura, empleando la fórmula empírica.

Se cambia la temperatura, y se vuelve a repetir la medida de la viscosidad. Se comprueba que el resultado coincide con el calculado a partir de la fórmula empírica.

Se aconseja al lector, que represente en un papel la viscosidad η de la glicerina en función de la temperatura T. Para que perciba el acusado cambio de esta magnitud cuando se incrementa ligeramente la temperatura.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Stautberg M, Fazio F, Russotto M, Wilkosz A. Using the Atwood machine to study Stokes' law. Am. J. Phys. 54 (10) October 1986, pp. 904-906