Caída libre desde distancias grandes.

Examinamos la situación más simple, aquella en la que el momento angular L=0, (movimiento rectilíneo) y solamente es

necesario aplicar el principio de conservación de la energía.

En el capítulo de Cinemática, hemos estudiado el movimiento de caída de los cuerpos, suponiendo que partían desde una altura h<<R pequeña en comparación con el radio de la Tierra. El tiempo t y la velocidad v con la el cuerpo que llega a la superficie de la Tierra se calculan mediante las ecuaciones.

$h = \frac{1}{2} g t^{2} v = g t$

Donde g es la aceleración de la gravedad en la superficie de la Tierra que supondremos constante.

$g = G \frac{M}{R^{2}} = 9.83 {m/s}^{2}$

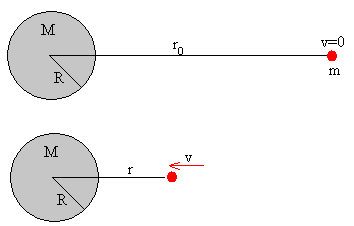
Vamos a describir el movimiento de un cuerpo que se deja caer desde una distancia r₀>R del centro de la Tierra, hasta que llega a su superficie. Como la fuerza de atracción, depende de la distancia r entre el centro de la Tierra y el objeto, la aceleración no es constante. Sin embargo, el principio de conservación de la energía nos permite calcular la velocidad v con la que llegará a dicha posición r.

$\frac{1}{2} m v^{2} - G \frac{m M}{r} = - G \frac{m M}{r_{0}} v = \sqrt{\frac{2 G M}{r_{0}} \frac{(r_{0} - r)}{r}}$

Para calcular el tiempo que tarda en llegar a la superficie escribimos v=-dr/dt, ya que r disminuye cuando v aumenta.

$t = - \int_{r}^{R} \frac{d r}{v} = - \sqrt{\frac{R}{2 G M}} \int_{r_{0}}^{r} \sqrt{\frac{r}{r_{0} - R}} d r = - \sqrt{\frac{r_{0}^{3}}{2 G M}} \int_{1}^{x} \sqrt{\frac{x}{1 - x}} d x$

Se ha escrito la integral en términos de la variable adimensional r=x·r₀. Se efectúa el cambio de variable

$z^{2} = \frac{x}{x - 1} d x = \frac{- 2 z \cdot d z}{{(z^{2} - 1)}^{2}}$

Se integra por partes

$\int \sqrt{\frac{x}{1 - x}} d x = 2 \int \frac{z^{2}}{{(z^{2} + 1)}^{2}} d z = \frac{- z}{z^{2} + 1} + \arctan z$

Se evalúa el integrando para los límites superior e inferior. $\begin{array}{l} \int_{1}^{x} \sqrt{\frac{x}{x - 1}} d x = - \sqrt{x - x^{2}} + \arctan {\sqrt{\frac{x}{x - 1}} |}_{1}^{x} = - \sqrt{x - x^{2}} + \arctan \sqrt{\frac{x}{x - 1}} - \frac{π}{2} = \\ - \sqrt{x - x^{2}} - \arccos \sqrt{x} \end{array}$

El tiempo t que tarda en llegar el móvil a la superficie de la Tierra es

$t = \sqrt{\frac{r_{0}^{3}}{2 G M}} (\sqrt{x - x^{2}} + \arccos \sqrt{x}) x = \frac{r}{r_{0}}$

Ejemplo 1:

Se deja caer un objeto situado a h=20000 km de altura. Calcular el tiempo que tarda en llegar a la superficie de la Tierra, y la velocidad con la que llega. Los datos son:

Radio de la Tierra R=6.37·10⁶ m

Masa de la Tierra M=5.98·10²⁴ kg
Constante G=6.67·10^-11 Nm²/kg²

r₀=R+h=26.37·10⁶ m, x=R/r₀=0.24 el tiempo t=7120 s

Aplicando el principio de conservación de la energía, obtenemos la velocidad con la que el objeto llega a la superficie de la Tierra es v=9746 m/s

Un cuerpo se deja caer desde una altura de h=20 km. Comparamos las predicciones de la Cinemática y de la Dinámica.

Cinemática: h=gt²/2 donde g=9.83 m/s² es la aceleración de la gravedad en la superficie de la Tierra, t=63.8 s, y la velocidad v=627 m/s
Dinámica: r₀=R+h=6.39·10⁶ m, x=R/r₀=0.997 el tiempo t=64.0 s. El principio de conservación de la energía, nos proporciona el valor de la velocidad v=626 m/s

Ejemplo 2:

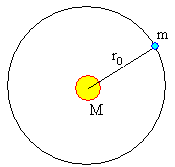Se envían al espacio exterior residuos procedentes de plantas nucleares, se reduce a cero su velocidad, permitíendoles que caigan libremente hacia el Sol a lo largo de la dirección radial. Calcular el tiempo que tardan en llegar a la superficie del Sol. Datos:

Masa del Sol, M=1.98·10³⁰ kg

Radio del Sol, R=6.96·10⁸ m

Radio de la órbita de la Tierra r₀=149.6·10⁹ m
Constante G=6.67·10^-11 Nm²/kg²

Con x=R/r₀=0.00465, t=5.59·10⁶ s=64.7 días.

Aplicando el principio de conservación de la energía obtenemos la velocidad del centro de la Tierra cuando llega a la superficie del Sol, v=614 601 m/s.

Órbitas en una dimensión

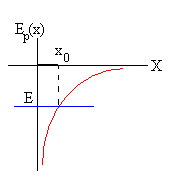Supongamos un cuerpo celeste de masa m es atraído por otro cuerpo de masa M situado en el origen.Su energía potencial es E_p(x)=-GMm/x (curva en color rojo) . Si su energía total es E≤0 (recta azul), se mueve en el segmento comprendido entre –x₀ y x₀, atravesando el origen con velocidad infinita. Estudiaremos su movimiento para x>0
En la posición extrema x₀, la velocidad del cuerpo es cero de modo que la energía del cuerpo es solamente potencial.

$E = - G \frac{m M}{x_{0}}$

La velocidad del cuerpo en cualquier otra posición 0<x≤x₀ es

$\frac{1}{2} m v^{2} - G \frac{m M}{x} = E$

Integramos la ecuación del movimiento, para determinar la posición del cuerpo x en función del tiempo t.

$\begin{array}{l} v = \frac{d x}{d t} = \pm \sqrt{2 (\frac{E}{m} + \frac{G M}{x})} a = \frac{| E |}{m} b = G M \\ \int_{x_{0}}^{x} \frac{d x}{\sqrt{\frac{b}{x} - a}} = \pm \sqrt{2} \int_{0}^{t} d t \int_{x_{0}}^{x} \frac{\sqrt{x} d x}{\sqrt{1 - \frac{a}{b} x}} = \pm \sqrt{2 b} t \end{array}$

Se hace el cambio de variable u²=ax/b

$2 \frac{b}{a} \sqrt{\frac{b}{a}} \int \frac{u^{2}}{\sqrt{1 - u^{2}}} d u$

Se hace el cambio de variable u=siny, se integra y se deshacen los cambios

$\begin{array}{l} 2 \frac{b}{a} \sqrt{\frac{b}{a}} \int \sin^{2} y \cdot d y = 2 \frac{b}{a} \sqrt{\frac{b}{a}} \int \frac{1 - \cos (2 y)}{2} d y = 2 \frac{b}{a} \sqrt{\frac{b}{a}} (\frac{1}{2} y - \frac{1}{4} \sin (2 y)) = \\ \frac{b}{a} \sqrt{\frac{b}{a}} (\arcsin \sqrt{\frac{a}{b} x} - \frac{1}{2} \sin (2 \arcsin \sqrt{\frac{a}{b} x})) \end{array}$

El resultado final es

$\begin{array}{l} \int_{x_{0}}^{x} \frac{\sqrt{x} d x}{\sqrt{1 - \frac{a}{b} x}} = \pm \sqrt{2 b} t \\ F (x) - F (x_{0}) = - \frac{a \sqrt{2 a}}{b} t \\ F (x) = \arcsin \sqrt{\frac{a}{b} x} - \frac{1}{2} \sin (2 \arcsin \sqrt{\frac{a}{b} x}) \end{array}$

Ejemplo:
El cuerpo de masa m cae libremente hacia el origen desde una distancia x₀.

$\begin{array}{l} | E | = G \frac{M m}{x_{0}} a = \frac{G M}{x_{0}} b = G M \\ F (x) = \arcsin \sqrt{\frac{x}{x_{0}}} - \frac{1}{2} \sin (2 \arcsin \sqrt{\frac{x}{x_{0}}}) \\ F (x_{0}) - F (x) = \frac{1}{x_{0}} \sqrt{\frac{2 G M}{x_{0}}} t \end{array}$

Datos del ejemplo 2 de la sección anterior
x=6.96·10⁸ m
x₀=149.6·10⁹ m
G=6.67·10^-11
M=1.98·10³⁰

Obtenemos t= 5.5918·10⁶ s
Para que llegue al centro del Sol x=0,
F(x)=0, F(x₀)=π/2

$t = \frac{π x_{0}}{2} \sqrt{\frac{x_{0}}{2 G M}}$

obtenemos t=5.5925·10⁶ s

Actividades

Se introduce

La altura en km del objeto por encima de la superficie de la Tierra, en el control de edición titulado Altura

Se pulsa el botón titulado EmpiezaSe observa el movimiento de caída del objeto. El programa interactivo proporciona en cada instante t

La altura en km del objeto sobre la superficie de la Tierra
Su velocidad en m/s

Referencias

Van Wyk S. Solution to the problem on p. 913. Am. J. Phys. 54 (10) October 1986, pp. 954

McCall M. Gravitational orbits in one dimension. Am. J. Phys. 74 (12) December 2006, pp. 1115-1119