La Luna

Trayectoria de la Luna alrededor del Sol

Supongamos que la Tierra describe una órbita circular alrededor del Sol de radio R con velocidad angular constante Ω, y la Luna describe una órbita circular alrededor de la Tierra de radio r y con velocidad angular constante ω. Se tratará de determinar la trayectoria seguida por la Luna respecto de un observador imaginariamente situado en el Sol.

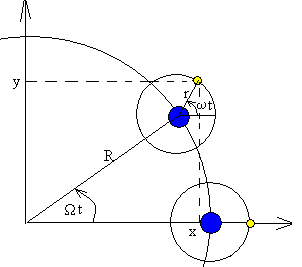
Como vemos en la figura, la posición de la Luna, situando el Sistema de Referencia en el Sol es.

x(t)=R·cos(Ωt)+r·cos(ωt)
y(t)= R·sin(Ωt)+r·sin(ωt)

Las componentes de la velocidad son

v_x=-RΩ·sin(Ωt)-rω·sin(ωt)
v_y=RΩ·cos(Ωt)+rω·cos(ωt)

Las componentes de la aceleración son

a_x=-RΩ²·cos(Ωt)-rω²·cos(ωt)
a_y=-RΩ²·sin(Ωt)-rω²·sin(ωt)

Como vimos en el estudio del movimiento curvilíneo, la componente normal de la aceleración es.

$a_{n} = \frac{a_{x} v_{y} - a_{y} v_{x}}{\sqrt{v_{x}^{2} + v_{y}^{2}}}$

La aceleración normal está dirigida hacia el centro de curvatura.

$a_{n} = - \frac{R^{2} Ω^{3} + r^{2} ω^{3} + r R Ω ω (Ω + ω) \cos (Ω - ω) t}{\sqrt{R^{2} Ω^{2} + r^{2} ω^{2} + 2 R r Ω ω \cos (Ω - ω) t}}$

El denominador es positivo, ya que es el módulo de la velocidad v. El numerador es positivo para cualquier valor de t si se cumple que

R²Ω³+r²ω³>rRΩω(Ω+ω)

o bien si

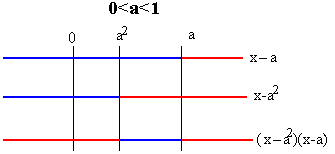$\begin{array}{l} (\frac{r}{R} - \frac{Ω^{2}}{ω^{2}}) (\frac{r}{R} - \frac{Ω}{ω}) > 0 \\ (x - a^{2}) (x - a) > 0 \end{array}$

Resolviendo esta inecuación sencilla se encuentra que la desigualdad se cumple (en color rojo en la figura) para

x>a y para x<a²

La aceleración normal no cambia de signo para cualquier valor de t, para $\frac{r}{R} > \frac{Ω}{ω}$ y para $\frac{r}{R} < \frac{Ω^{2}}{ω^{2}}$
Para $\frac{r}{R} < \frac{Ω^{2}}{ω^{2}}$ se producen cambios de signo en el numerador y por tanto, en la aceleración normal, a_n. La trayectoria presenta lazos.
Cuando $\frac{Ω}{ω} = \frac{r}{R}$ el numerador y el denominador se anulan a la vez en determinados instantes t, como puede fácilmente adivinarse en la expresión de la aceleración normal. La trayectoria presenta cúspides donde la curvatura no está definida.

$a_{n} = - \frac{R Ω (Ω + ω) (1 + \cos (Ω - ω) t)}{\sqrt{2 (1 + \cos (Ω - ω) t})}$

Los datos del sistema Sol-Tierra-Luna son

La velocidad angular de la Tierra alrededor del Sol es Ω=2π/365 dias^-1 y
La velocidad angular de la Luna alrededor de la Tierra es ω=2π/27.3 dias^-1
El radio de la órbita de la Tierra es R=1.496·10⁸ km
El radio de la órbita de la Luna es r=3.84·10⁵ km

Con estos datos r/R=0.0026, Ω/ω =0.075, Ω²/ω²=0.0056. Estamos en el caso r/R< Ω²/ω², o bien, ω²r< Ω²R

La aceleración normal tiene el mismo signo para cualquier valor de t, y apunta hacia el Sol. Esto debe ser así, ya que la fuerza de atracción de la Tierra sobre la Luna es ocho veces menor que la fuerza de atracción del Sol sobre la Luna, la fuerza resultante y por tanto, la aceleración están dirigidos hacia el Sol, la trayectoria de la Luna no puede formar lazos.

Discusión

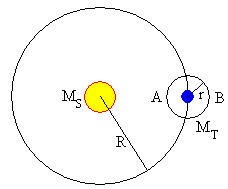Cuando la Luna se encuentra en el punto B, las dos aceleraciones debidas al movimiento circular de la Tierra alrededor del Sol y de la Luna alrededor de la Tierra se suman, y apuntan hacia el centro del Sol.

a_n=Ω²R+ω²r

Cuando la Luna se encuentra en A, las dos aceleraciones tienen signos contrarios

a_n=Ω²R-ω²r

pero como Ω²R>ω²r la aceleración a_n sigue apuntando hacia el Sol

De la dinámica del movimiento circular uniforme tenemos que

$G \frac{M_{s} M_{T}}{R^{2}} = M_{T} Ω^{2} R G \frac{M_{T} M_{L}}{r^{2}} = M_{L} ω^{2} r$

La desigualdad Ω²R>ω²r equivale a

$Ω^{2} R > ω^{2} r \frac{M_{S}}{R^{2}} > \frac{M_{T}}{r^{2}} r > R \sqrt{\frac{M_{T}}{M_{S}}}$

La aceleración debida a la atracción del Sol, supera a la atracción de la Tierra o bien, el radio de la órbita de la Luna alrededor de la Tierra es mayor que el valor crítico $R \sqrt{M_{T} / M_{S}}$

Comprobamos si otros satélites de los planetas del Sistema Solar cumplen esta condición

R es el radio de la órbita del planeta alrededor del Sol, supuesta circular,
M_s=1.98·10³⁰ kg es la masa del Sol,
M_T es la masa del planeta
r es el radio de la órbita del satélite del satélite alrededor del planeta, supuesta circular

Planeta (Satélite)	Datos del planeta	Satélite	$R \sqrt{M_{T} / M_{S}}$	Comentario
Tierra (Luna)	M_T=5.98·10²⁴ kg R=1.496·10¹¹ m	r=384.4·10⁶	260.0·10⁶m	La Luna "cae" hacia el Sol
Marte (Deimos)	M_T=6.58·10²³ kg R=2.28·10¹¹ m	r=23.46·10⁶ m	131.4·10⁶ m	Deimos "cae" hacia Marte
Júpiter (Calisto)	M_T=1.90·10²⁷ kg R=7.78·10¹¹ m	r=1880·10⁶ m	24122·10⁶ m	Calisto "cae" hacia Júpiter
Saturno (Titán)	M_T=5.69·10²⁶ kg R=14.27·10¹¹ m	r=1222·10⁶ m	24185·10⁶ m	Titán "cae" hacia Saturno
Neptuno (Tritón)	M_T=1.03·10²⁶ kg R=44.97·10¹¹ m	r=394.7·10⁶ m	32410·10⁶ m	Tritón "cae" hacia Neptuno

La Luna es el único entre todos los satélites de los planetas cuyo radio de su órbita supera el valor límite $R \sqrt{M_{T} / M_{S}}$ , lo que implica que la aceleración debida a la atracción del Sol, es mayor que la debida al planeta que orbita. Decimos que la Luna "cae" hacia el Sol

Actividades

Se introduce

El cociente r/R (radio de la órbita de la Luna dividido el radio de la órbita de la Tierra), actuando en la barra de desplazamiento titulada rLuna/rTierra.
El cociente Ω/ω (velocidad angular de la Tierra dividido la velocidad angular de la Luna en su órbita alrededor de la Tierra), actuando en la barra de desplazamiento titulada wTierra/wLuna.

Se pulsa en el botón titulado Empieza

La velocidad angular de la Luna en su órbita alrededor de la Tierra se ha fijado en el valor ω=1.
El radio de la órbita de la Tierra alrededor del Sol se ha fijado en el valor R=1.

Se observa en color azul la órbita circular de la Tierra en cuyo centro está el Sol, y en color rojo la trayectoria de la Luna alrededor del Sol para distintos valores de los cocientes r/R y Ω/ω que seleccionamos en las barras de desplazamiento respectivas.

CinemaApplet1 aparecerá en un explorador compatible con JDK 1.1.

Referencias

Amengual A. Sobre la órbita heliocéntrica de la Luna. Revista Española de Física, Vol 16, nº 5, 2002., págs. 50-51