Movimiento curvilíneo

Componentes tangencial y normal de la aceleración

Las componentes rectangulares de la aceleración no tienen significado físico, pero si lo tienen las componentes de la aceleración en un nuevo sistema de referencia formado por la tangente a la trayectoria y la normal a la misma.

Hallar las componentes tangencial y normal de la aceleración en un determinado instante es un simple problema de geometría, tal como se ve en la figura.

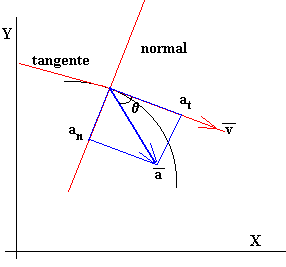
Se dibujan los ejes horizontal X y vertical Y.

Se calculan las componentes rectangulares de la velocidad y de la aceleración en dicho instante. Se representan los vectores velocidad y aceleración en dicho sistema de referencia.

Se dibujan los nuevos ejes, la dirección tangencial es la misma que la dirección de la velocidad, la dirección normal es perpendicular a la dirección tangencial.

Con la regla y el cartabón se proyecta el vector aceleración sobre la dirección tangencial y sobre la dirección normal.

Se determina el ángulo θ entre el vector velocidad y el vector aceleración, y se calcula el valor numérico de dichas componentes: a_t=a cosθ y a_n=a sinθ

Ejemplo:

El vector velocidad del movimiento de una partícula viene dado por v=(3t-2)i+(6t²-5)j m/s. Calcular las componentes tangencial y normal de la aceleración en el instante t=2 s. Dibujar el vector velocidad, el vector aceleración y las componentes tangencial y normal en dicho instante.

Dadas las componentes de la velocidad obtenemos las componentes de la aceleración

v_x =3t-2 m/s, a_x=3 m/s²v_y=6t²-5 m/s, a_y=12t m/s²

Los valores de dichas componentes en el instante t=2 s son

v_x =4 m/s, a_x=3 m/s²v_y=19 m/s, a_y=24 m/s²

Dibujamos el vector velocidad y el vector aceleración

Calculamos el módulo de la aceleración a y el ángulo θ que forman el vector velocidad y el vector aceleración.

\begin{array}{l} θ = \arctan \frac{a_{y}}{a_{x}} - \arctan \frac{v_{y}}{v_{x}} = 4.76 º \\ a = \sqrt{a_{x}^{2} + a_{y}^{2}} = 24.2 \end{array}

Se calculan las componentes tangencial y normal de la aceleración

a_t=a·cosθ =24.1 m/s²
a_n=a·sinθ=2.0 m/s²

Podemos hallar la aceleración tangencial en cualquier instante, a partir del producto escalar del vector aceleración a y el vector velocidad v.

$\begin{array}{l} v \cdot a = v a \cos θ = v a_{t} \\ a_{t} = \frac{v \cdot a}{v} = \frac{v_{x} a_{x} + v_{y} a_{y}}{\sqrt{v_{x}^{2} + v_{y}^{2}}} \end{array}$

La aceleración normal, se obtiene a partir del módulo de la aceleración a y de la aceleración tangencial a_t

$\begin{array}{l} a_{n}^{2} = a^{2} - a_{t}^{2} = a_{x}^{2} + a_{y}^{2} - \frac{{(v_{x} a_{x} + v_{y} a_{y})}^{2}}{v_{x}^{2} + v_{y}^{2}} \\ a_{n} = \frac{a_{x} v_{y} - a_{y} v_{x}}{\sqrt{v_{x}^{2} + v_{y}^{2}}} \end{array}$

Radio de curvatura

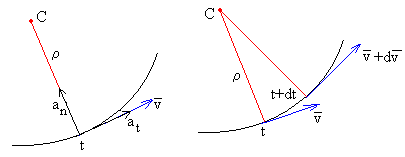
En la figura, se muestra el radio de curvatura y el centro de curvatura de una trayectoria cualesquiera en el instante t. Se dibuja la dirección del vector velocidad v en el instante t, la dirección del vector velocidad v+dv en el instante t+dt. Se trazan rectas perpendiculares a ambas direcciones, que se encuentran en el punto C denominado centro de curvatura. La distancia ente entre la posición del móvil en el instante t, y el centro de curvatura C es el radio de curvatura ρ.

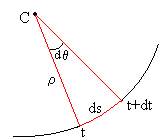En el intervalo de tiempo comprendido entre t y t+dt, la dirección del vector velocidad cambia un ángulo dθ. que es el ángulo entre las tangentes o entre las normales. El móvil se desplaza en este intervalo de tiempo un arco ds=ρ·dθ, tal como se aprecia en la figura.

Otra forma de obtener las componentes tangencial y normal de la aceleración, es la de escribir el vector velocidad v como producto de su módulo v por un vector unitario que tenga su misma dirección y sentido u_t=v/v. La derivada de un producto se compone de la suma de dos términos

$a = \frac{d v}{d t} = \frac{d (v \cdot u_{t})}{d t} = \frac{d v}{d t} u_{t} + v \frac{d u_{t}}{d t}$

El primer término, tiene la dirección de la velocidad o del vector unitario u_t, es la componente tangencial de la aceleración

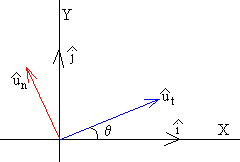El segundo término, vamos a demostrar que tiene la dirección normal u_n. Como vemos en la figura las componentes del vector unitario u_t son

u_t=cosθ·i+sinθ·j

Su derivada es

$\frac{d u_{t}}{d t} = (- \sin θ i + \cos θ j) \frac{d θ}{d t} = \frac{d θ}{d t} u_{n} = \frac{1}{ρ} \frac{d s}{d t} u_{n} = \frac{v}{ρ} u_{n}$

El vector aceleración es

$a = \frac{d v}{d t} = \frac{d v}{d t} u_{t} + \frac{v^{2}}{ρ} u_{n}$

Las componentes tangencial y normal de la aceleración valen, respectivamente

$a_{t} = \frac{d v}{d t} a_{n} = \frac{v^{2}}{ρ}$

Esta última fórmula, la obtendremos de una forma más simple para una partícula que describe un movimiento circular uniforme.

Como la velocidad es un vector, y un vector tiene módulo y dirección. Existirá aceleración siempre que cambie con el tiempo bien el módulo de la velocidad, la dirección de la velocidad o ambas cosas a la vez.

Si solamente cambia el módulo de la velocidad con el tiempo, como en un movimiento rectilíneo, tenemos únicamente aceleración tangencial.
Si solamente cambia la dirección de la velocidad con el tiempo, pero su módulo permanece constante como en un movimiento circular uniforme, tenemos únicamente aceleración normal.
Si cambia el módulo y la dirección de la velocidad con el tiempo, como en un tiro parabólico, tendremos aceleración tangencial y aceleración normal..