Péndulo accionado por las fuerzas de marea

El origen de las fuerza de marea se debe a que la Tierra es un cuerpo extenso y el campo gravitatorio producido por la Luna o por el Sol no es homogéneo en todos sus puntos, ya que hay unos puntos que están más cercanos y otros más alejados de dichos cuerpos celestes.

En esta página, se explica los efectos de las fuerzas de marea producidos por la Tierra sobre un sistema muy simple, que consiste en una varilla rígida, de longitud 2l que supondremos de masa despreciable, en cuyos extremos hay dos masas puntuales iguales.

Descripción

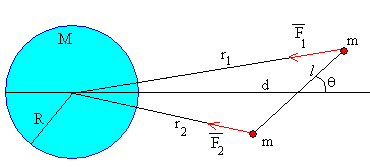
La masa de la Tierra es M, y su radio es R. En el espacio hay una varilla de masa despreciable de longitud 2l cuyo centro dista d del centro de la Tierra. En los extremos de la varilla hay dos masas m puntuales iguales. El sistema puede oscilar libremente en el plano de la figura alrededor del centro de masa de la varilla.

Las masas puntuales distan del centro de la Tierra r₁ y r₂ respectivamente

$\begin{array}{l} r_{1}^{2} = {(R + l \cdot \cos θ)}^{2} + {(l \cdot sin θ)}^{2} = R^{2} + l^{2} + 2 l R \cos θ \\ r_{2}^{2} = {(R - l \cdot \cos θ)}^{2} + {(l \cdot sin θ)}^{2} = R^{2} + l^{2} - 2 l R \cos θ \end{array}$

Las fuerzas que ejerce la Tierra sobre cada una de las masas puntuales tienen por módulo

$F_{1} = G \frac{M m}{r_{1}^{2}} F_{2} = G \frac{M m}{r_{2}^{2}}$

la dirección es a lo largo de la recta que une el centro de la Tierra y cada una de las masas puntuales, y de sentido hacia el centro de la Tierra.

El momento de las fuerzas F₁ y F₂ respecto del centro de la varilla es

M=F₁·l·sin(θ-α₁)-F₂·l·sin(θ+α₂)

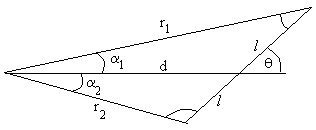
Aplicando el teorema del seno

$\frac{r_{1}}{sin(180- θ)} = \frac{d}{sin (θ - α_{1})} \frac{r_{2}}{sin θ} = \frac{d}{sin (180 - θ + α_{2})}$

La ecuación del movimiento de rotación alrededor del centro de la varilla es

$I \frac{d^{2} θ}{d t^{2}} = G \frac{M m}{r_{1}^{2}} l \frac{d sin θ}{r_{1}} - \frac{M m}{r_{2}^{2}} l \frac{d sin θ}{r_{2}}$

El momento de inercia de las dos masas puntuales, respecto del eje de rotación perpendicular a a varilla y que pasa por su c.m. es I=2ml²

$\frac{d^{2} θ}{d t^{2}} = \frac{G M \cdot d \cdot sin θ}{2 l} (\frac{1}{r_{1}^{3}} - \frac{1}{r_{2}^{3}})$

Se resuelve la ecuación diferencial del movimiento por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, θ=π/6, dθ/dt=0

Aproximaciones

Supongamos que la longitud de la varilla 2l es pequeña en comparación con la distancia d entre el centro de la Tierra y el c.m. de la varilla.

$\frac{1}{r_{1}^{3}} = \frac{1}{d^{3}} {(1 + \frac{l^{2}}{d^{2}} + 2 \frac{l}{d} \cos θ)}^{- 3 / 2} \approx \frac{1}{d^{3}} (1 - 3 \frac{l}{d} \cos θ)$

despreciando los términos en l²/d² en adelante. Del mismo modo

$\frac{1}{r_{2}^{3}} = \frac{1}{d^{3}} {(1 + \frac{l^{2}}{d^{2}} - 2 \frac{l}{d} \cos θ)}^{- 3 / 2} \approx \frac{1}{d^{3}} (1 + 3 \frac{l}{d} \cos θ)$

La ecuación del movimiento se puede aproximar a

$\frac{d^{2} θ}{d t^{2}} = - \frac{3 G M \cdot sin θ \cdot \cos θ}{d^{3}}$

o bien

$\frac{d^{2} (2 θ)}{d t^{2}} + \frac{3 G M \cdot}{d^{3}} sin(2 θ) = 0$

Esta es una ecuación similar a la del péndulo simple, en vez del ángulo θ, que hace el hilo con la vertical aparece el ángulo 2θ.

Suponiendo que el péndulo oscila con una pequeña amplitud angular, aproximamos sin(2θ)≈(2θ). Obtenemos la ecuación diferencial de un MAS

$\frac{d^{2} (2 θ)}{d t^{2}} + \frac{3 G M \cdot}{d^{3}} (2 θ) = 0$

de periodo

$P = \frac{2 π}{ω} = 2 π \sqrt{\frac{d^{3}}{3 G M}}$

El periodo es independiente de la longitud l del péndulo, esto indica que las fuerzas de marea se manifiestan también en sistemas cuyo tamaño es pequeño.

Si el péndulo se coloca en la superficie de la Tierra d=6370 km, M=5.98·10²⁴ kg, G=6.67·10^-11 Nm²/kg²

El periodo P=2920.2 s=48.7 min

Actividades

Se introduce

La longitud 2l/R del péndulo, actuando en la barra de desplazamiento titulada Longitud péndulo.
La distancia d/R del centro de la Tierra al c.m. de la varilla, actuando en la barra de desplazamiento titulada Distancia.

Se pulsa el botón titulado Empieza

El programa no prosigue si d-l<R e invita al usuario a aumentar la distancia d/R o a disminuir la longitud 2l/R del péndulo.

El programa interactivo resuelve por el procedimiento numérico de Runge-Kutta la ecuación diferencial del movimiento con las siguientes condiciones iniciales: en el instante t=0, θ=π/6, dθ/dt=0. En la parte superior del applet, se proporcionan los datos del tiempo t en minutos y del ángulo θ en grados.

Referencias

Grǿn Ǿ. A tidal force pendulum. Am. J. Phys. 51 (5) May 1983, pp. 429-431