Tiros frontales a canasta

Margen de error

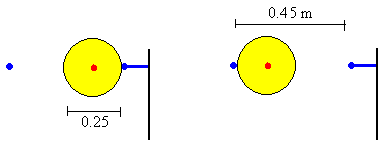
En los apartados anteriores, hemos supuesto que el punto de impacto situado a una distancia L y a una altura h del punto de lanzamiento es único. Como el diámetro del balón es menor que el diámetro del aro, vamos a ver que existe una indeterminación en el alcance L, que da lugar a una tolerancia en la velocidad inicial v₀, en el ángulo de tiro θ₀ o en ambos a la vez. Por tanto, la velocidad inicial de lanzamiento y el ángulo de tiro que dan lugar a enceste pueden cambiar en un pequeño intervalo que depende de la posición inicial del balón respecto del aro.

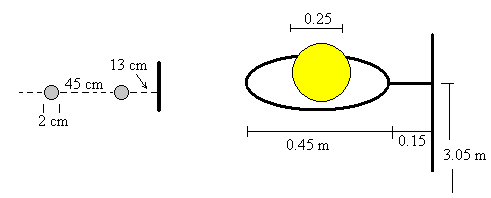
Podríamos pensar que la indeterminación en el alcance es igual a la diferencia entre el diámetro del balón y el diámetro del aro, tal como se muestra en la figura. Sin embargo, el balón entra en el aro siguiendo una trayectoria cuya tangente forma un ángulo θ_e con la horizontal.

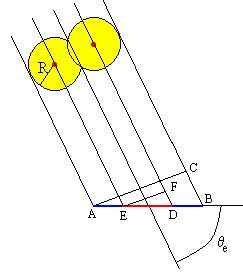
En la figura, el aro AB es atravesado por un balón cuya dirección de su velocidad forma un ángulo θ_e con la horizontal. En los triángulos rectángulos ABC y EDF

AC=D_a·sin|θ_e|

EF=AC-2·R= D_a·sin|θ_e|-2R

ED=2ΔL=EF/sin|θ_e|

$Δ L = \frac{1}{2} (D_{a} - \frac{2 R}{sin| θ_{e} |})$

ΔL (en color rojo) representa el margen de error en la distancia horizontal L desde el punto de lanzamiento hasta el blanco. Este margen de error desaparece cuando ΔL=0, es decir, cuando

$sin | θ_{e} | = \frac{2 R}{D_{a}} = \frac{25}{45} | θ_{e} | = 33.7 º$

Como ya se ha explicado, el ángulo θ_e que forma el vector velocidad v con la horizontal debe se mayor (en valor absoluto) que 33.7º para que el balón entre por el aro, sin tocarlo.

Fijado el ángulo de tiro θ₀> θ₀_Lla velocidad inicial v₀ no es única sino que está comprendida en el intervalo v₀+Δv₊ y v₀-Δv_-.Estos intervalos se calculan del siguiente modo.

En la fórmula,

$v_{0}^{2} = \frac{g L (1 + \tan^{2} θ_{0})}{2 (\tan θ_{0} - h / L)}$

con los datos de h y L calculamos v₀ para un determinado ángulo de disparo θ₀

Sustituimos L por L+ΔL y calculamos la velocidad de disparo v₊= v₀+Δv₊

Sustituimos L por L-ΔL y calculamos la velocidad de disparo v_-= v₀-Δv_-

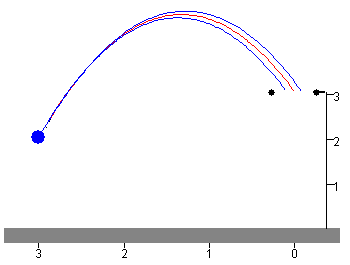
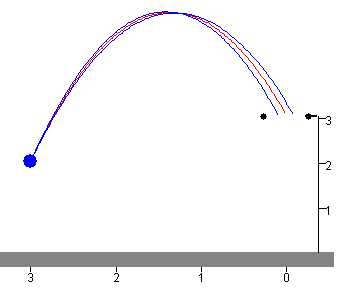
En la figura, se muestra las tres trayectorias:

En color rojo, la que pasa por el centro del aro,

En color azul, las que pasan por L+ΔL y por L-ΔL

Fijada la velocidad de disparo v₀, el ángulo de tiro no es único sino que está comprendida en el intervalo θ₀+Δ θ₊ y θ₀-Δ θ_-. Estos intervalos se calculan del siguiente modo.

Resolvemos la ecuación de segundo grado en tanθ₀.

$\tan^{2} θ_{0} - \frac{2 v_{0}^{2}}{g L} \tan θ_{0} + (1 + \frac{2 v_{0}^{2} h}{g L^{2}}) = 0$

con los datos de h y L calculamos el ángulo de tiro θ₀ para una determinada velocidad de disparo v₀.

Sustituimos L por L+ΔL y calculamos el ángulo de tiro θ₊= θ₀+Δθ₊

Sustituimos L por L-ΔL y calculamos el ángulo de tiro θ_-= θ₀-Δθ_-

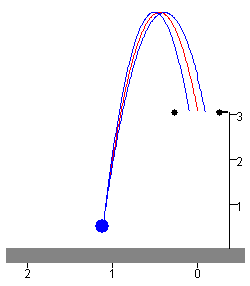
En la figura, se muestra las tres trayectorias:

En color rojo, la que pasa por el centro del aro,

En color azul, las que pasan por L+ΔL y por L-ΔL

Estos dos márgenes de error sirven de criterio para elegir la mejor trayectoria. Cuando mayor sea el margen de error para un determinado ángulo de tiro, mayor es la libertad del jugador para desviarse de los valores precisos de v₀ y θ₀ necesarios para que el balón entre por el centro del aro.

Ejemplo:

Supongamos, como en el ejemplo del apartado anterior, que h=1 m y L=3 m.

Fijamos el ángulo de tiro θ₀=70º, la velocidad inicial calculada v₀=7.21 m/s.
El ángulo de entrada del balón cuando llega al aro es

$\tan θ_{e} = \frac{2 \cdot 1}{3} - \tan 70 º θ_{e} = - 64.3 º$

El margen de error ΔL en la distancia horizontal L vale

$Δ L = \frac{1}{2} (0.45 - \frac{0.25}{sin64 .3}) = 0.086 m$

En la fórmula,

$v_{0}^{2} = \frac{g L (1 + \tan^{2} θ_{0})}{2 (\tan θ_{0} - h / L)}$

Sustituimos L por L+ΔL=3.086 y calculamos la velocidad inicial v₊=7.30 m/s, y la tolerancia Δv₊=0.09 m/s
Sustituimos L por L-ΔL=2.914 y calculamos la velocidad inicial v_-= 7.12 m/s, y la tolerancia Δv_-=0.09 m/s

Fijamos la velocidad inicial v₀=8.0 m/s, el ángulo de tiro calculado es θ₀=74.83º
En la ecuación de segundo grado

$\tan^{2} θ_{0} - \frac{2 v_{0}^{2}}{g L} \tan θ_{0} + (1 + \frac{2 v_{0}^{2} h}{g L^{2}}) = 0$

Sustituimos L por L+ΔL=3.086 y calculamos el ángulo de tiro θ_-=74.34º, y la tolerancia Δ θ_-=0.49º
Sustituimos L por L-ΔL=2.914 y calculamos el ángulo de tiro θ₊ =75.32º, y la tolerancia Δ θ₊=0.49º

Actividades

Se introduce las coordenadas del centro de la pelota:

La distancia x₀ de la pelota al centro del aro, actuando en la barra de desplazamiento titulada Distancia, o introduciendo un valor en el control de edición correspondiente.
La altura y₀ de la pelota sobre el suelo, actuando en la barra de desplazamiento titulada Altura o introduciendo un valor en el control de edición correspondiente.

Las coordenadas del centro (x₀, y₀) de la pelota se miden respecto de un Sistema de Referencia en el que el eje vertical Y pasa por el centro del aro, y el eje horizontal es el suelo.

Fijada la posición del punto de lanzamiento del balón: la distancia horizontal al blanco es L=x₀, y la altura h=3.05-y₀. Se representa, en la parte derecha del applet, la función que relaciona la velocidad inicial v₀ con el ángulo de tiro θ₀. y también se representa la función v₊(θ₀) y v_-(θ₀).

Con el puntero del ratón movemos un pequeño círculo de color azul para seleccionar:

el valor de la velocidad inicial v₀.
el valor del ángulo de tiro θ₀.

Se pulsa el botón titulado Empieza

Comprobar que las trayectorias que corresponden a pares de valores (v₀, θ₀) situados sobre la región coloreada, corresponden a trayectorias que pasan por el aro sin tocarlo.

CinemaApplet2 aparecerá en un explorador compatible con JDK 1.1.

Mueva con el puntero del ratón el círculo de color azul

Referencias

Brancazio P. J. Physics of basketball. Am. J. Phys. 49 (4) April 1981. pp. 356-365

Savirón J. M. Problemas de Física General en un año olímpico. Editorial Reverté (1984), págs. 113-157.