Un trozo de barro que se desprende de una rueda

Posición y velocidad en el instante t

Las componentes de la velocidad del cuerpo en el instante t son

$\begin{array}{l} v_{x} = v_{0} - v_{0} \sin ϕ \\ v_{y} = - v_{0} \cos ϕ - g (t - t_{0}) \end{array}$

La posición del cuerpo en el instante t es

$\begin{array}{l} x = x_{0} + v_{0 x} (t - t_{0}) = v_{0} t_{0} + R \cos ϕ + v_{0} (1 - \sin ϕ) (t - t_{0}) \\ y = y_{0} + v_{0 y} (t - t_{0}) - \frac{1}{2} g {(t - t_{0})}^{2} = R - R \sin ϕ - v_{0} \cos ϕ (t - t_{0}) - \frac{1}{2} g {(t - t_{0})}^{2} \end{array}$

Alcance y altura máxima

El cuerpo llega al suelo cuando y=0.

$t - t_{0} = \frac{- v_{0} \cos ϕ + \sqrt{v_{0}^{2} \cos^{2} ϕ + 2 g R (1 - \sin ϕ)}}{g} ϕ = \frac{v_{0}}{R} t_{0}$

Una vez calculado (t-t₀) se obtiene el alcance horizontal x_m

x_m= v₀·t₀-R·sinφ+ v₀(1-cosφ) ·(t-t₀)

La altura máxima se alcanza cuando v_y=0

$t - t_{0} = \frac{v_{0} \sin ϕ}{g}$

Para que este cociente sea positivo, el ángulo φ debe estar en el intervalo 0<φ<π. El cuerpo se lanza hacia arriba si el ángulo φ está en este intervalo

$y_{m} = R - R \cos ϕ + \frac{v_{0}^{2} \sin^{2} ϕ}{2 g}$

La altura y_m también se puede calcular aplicando el principio de conservación de la energía.

En la posición de lanzamiento y₀=R-Rcosφ las componentes de la velocidad del cuerpo son

v_0x=v₀-v₀·cosφ
v_0y= v₀·sinφ

La energía del cuerpo de masa m es

$E_{i} = \frac{1}{2} m (v_{0}^{2} \sin^{2} ϕ + v_{0 x}^{2}) + m g (R - R \cos ϕ)$

En la posición de máxima altura y_m la componente v_y=0 de la velocidad, la componente v_x no cambia. La energía E_f es

$E_{f} = \frac{1}{2} m v_{0 x}^{2} + m g y_{m}$

Aplicamos el principio de conservación de la energía E_i=E_f y despejamos y_m obteniendo el mismo resultado.

Máximo valor de la altura máxima

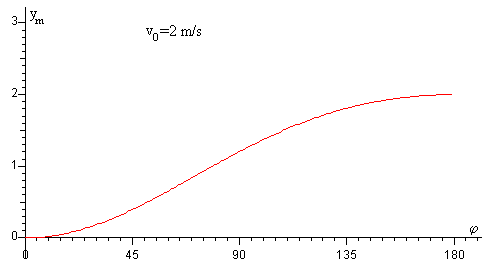
En la figura, se representa la altura máxima y_m que alcanza el trozo de barro en función del ángulo φ cuando la velocidad de traslación de la rueda es de v₀= 2 m/s. El radio de la rueda se ha fijado en R=1 m. El valor máximo de la altura máxima se alcanza cuando φ=π=180º

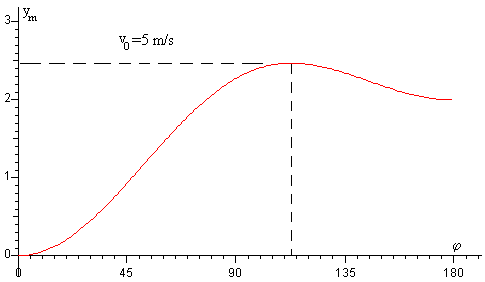
Cuando la velocidad de traslación de la rueda es de v₀= 5 m/s. El valor máximo de la altura máxima se alcanza cuando φ<π.

Calculamos el ángulo φ para el cual y_m presenta un máximo

$\frac{d y_{m}}{d ϕ} = R \sin ϕ + \frac{v_{0}^{2}}{g} \cos ϕ \cdot \sin ϕ = 0$

Esta ecuación tiene dos soluciones

La primera solución, se obtiene haciendo sinφ=0, φ=π, por lo que y_m=2R
La segunda solución, se obtiene haciendo

$\cos ϕ = - \frac{R g}{v_{0}^{2}}$

Para que el coseno sea menor que la unidad, en valor absoluto, se tiene que cumplir que $v_{0}^{2} > R g$

Para que el coseno sea negativo, y al la vez que la trayectoria sea hacia arriba implica que el ángulo φ debe de estar en el intervalo π/2<φ<π.

La máxima altura y_m alcanzada por el cuerpo que se desprende de esta posición es

$y_{m} = R + \frac{R^{2} g}{2 v_{0}^{2}} + \frac{v_{0}^{2}}{2 g}$

Ejemplo:

Se ha fijado el radio de la rueda en R =1 m
Si v₀=2 m/s
Si el trozo de barro se desprende cuando φ=π/2, el instante t₀ en el que se alcanza esta posición es t₀=φ·R/v₀=π/4=0.79 s

Calculamos la altura máxima y_m

$y_{m} = 1 - 1 \cdot \cos (\frac{π}{2}) + \frac{2^{2} \sin^{2} π}{2 \cdot 9.8} = 1.2 m$

Para v₀=5 m/s se cumple que 5²>1·9.8

El ángulo φ que hace que la altura y_m sea la máxima posible, véase la figura más arriba, es

$\begin{array}{l} \cos ϕ = - \frac{1 \cdot 9.8}{5^{2}} ϕ = 1.97 rad = 11 3º \\ y_{m} = 1 + \frac{1^{2} \cdot 9.8}{2 \cdot 5^{2}} + \frac{5^{2}}{2 \cdot 9.8} = 2.47 m \end{array}$

El instante t₀ en el que se alcanza esta posición es t₀=φ·R/v₀=1.97/5=0.39 s

Actividades

Se introduce

La velocidad v₀, del c.m. de la rueda actuando en la barra de desplazamiento titulada Velocidad.
El radio R de la rueda se ha fijado en R=1 m

Se pulsa el botón titulado Empieza

Cuando queremos que el trozo de barro se desprenda en una posición angular φ dada, o en un instante t₀. Se pulsa el botón titulado Pausa y a continuación, varias veces el botón titulado Paso hasta que veamos en la parte superior izquierda del applet que el contador de tiempo marque el instante deseado.

Pulsamos el botón titulado Desprende

Pulsamos el botón titulado Continua para observar la trayectoria, o bien, pulsamos varias veces el botón titulado Paso para acercarnos al instante en el que el cuerpo alcanza la máxima altura (la componente Y de su velocidad v_y=0). Anotamos la máxima altura y_m y la comparamos con los cálculos realizados a mano.

CinemaApplet2 aparecerá en un explorador compatible con JDK 1.1.

Referencias

Newby N. D., Mud thrown from a wheel: a critical speed. Am. J. Phys. 45 (11) November 1977, pp. 1116-1117

Goodman F. O. Mud thrown from a wheel again. Am. J. Phys. 63 (1) January 1995, pp. 82-8