Movimiento bajo la aceleración constante de la gravedad

Alcance horizontal y altura máxima

En el applet se trazan las trayectorias de proyectiles disparados con la misma velocidad inicial v₀ pero con los siguientes ángulos de tiro θ : 10º, 20º, 30º, 40º, 45º, 50º, 60º, 70º, 80º, 90º.

Las ecuaciones del movimiento de los proyectiles son

$\begin{array}{l} x = v_{0} \cos θ \cdot t \\ y = v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{array}$

La parábola de seguridad

El alcance horizontal de cada uno de los proyectiles se obtiene para y=0.

$x_{\max} = \frac{v_{0}^{2} sin (2 θ)}{g}$

Su valor máximo se obtiene para θ =45º, teniendo el mismo valor para θ =45+α , que para θ =45-α . Por ejemplo, tienen el mismo alcance los proyectiles disparados con ángulos de tiro de 30º y 60º, ya que sin(2·30)=sin(2·60).

La altura máxima que alcanza un proyectil se obtiene con v_y=0.

$y_{\max} = \frac{v_{0}^{2} {sin}^{2} θ}{2 g}$

Su valor máximo se obtiene para el ángulo de disparo θ =90º.

La envolvente de todas las trayectorias descritas por los proyectiles cuyo ángulo de disparo está comprendido entre 0 y 180º se denomina parábola de seguridad.

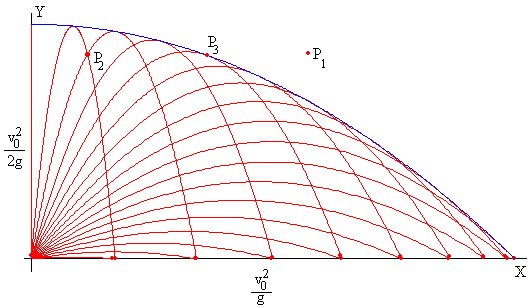
Esta denominación hace referencia al hecho de que fuera de esta parábola estamos a salvo de los proyectiles disparados con velocidad v₀.

Se trata de la parábola simétrica respecto del eje Y de ecuación y=-ax²+b que pasa por los puntos (x=v₀²/g, y=0), y (x=0, y=v₀²/(2g)) tal como se ve en la figura.

La ecuación de dicha parábola es

$y = - \frac{1}{2} \frac{g}{v_{0}^{2}} x^{2} + \frac{1}{2} \frac{v_{0}^{2}}{g}$

Deducción alternativa de la ecuación de la parábola de seguridad

Las ecuaciones paramétricas de la trayectoria son

$\begin{array}{l} x = v_{0} \cos θ \cdot t \\ y = v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{array}$

Eliminado el tiempo t, obtenemos la ecuación de la trayectoria

$y = x \tan θ - \frac{g x^{2}}{2 v_{0}^{2} \cos^{2} θ}$

Esta ecuación se puede escribir de forma alternativa

$\tan^{2} θ - \frac{2 v_{0}^{2}}{g x} \tan θ + (1 + \frac{2 v_{0}^{2} y}{g x^{2}}) = 0$

Consideremos un punto arbitrario P del plano. Sustituimos las coordenadas (x, y) del punto en la ecuación de la trayectoria y puede ocurrir

Que la ecuación de segundo grado en tanθ no tenga raíces reales. El punto P₁ no podría ser un punto de impacto para un proyectil disparado con velocidad inicial v₀.
Que la ecuación de segundo grado tenga dos raíces reales, lo que implicará que el punto P₂ es accesible, y que hay dos ángulos de tiro θ₁ y θ₂ que dan en el blanco P₂. En la figura, vemos que cualquier punto en el interior de la envolvente es alcanzado por dos trayectorias.
Cuando la raíz de la ecuación de segundo grado es doble θ₁=θ₂. Como vemos en la figura, solo hay una trayectoria que pasa por un punto P₃ dado de la envolvente.

Para que las raíces sean iguales, se tiene que cumplir que el discriminante b²-4ac de la ecuación de segundo grado ax²+bx+c=0 sea nulo.

${(\frac{2 v_{0}^{2}}{g x})}^{2} - 4 (1 + \frac{2 v_{0}^{2} y}{g x^{2}}) = 0 y = - \frac{g}{2 v_{0}^{2}} x^{2} + \frac{v_{0}^{2}}{2 g}$

Esta es la ecuación de la envolvente que hemos obtenido anteriormente.

Otra deducción alternativa es la siguiente:

La ecuación de la trayectoria depende del ángulo θ con el que se dispara el proyectil.
f(x, y, θ)=0

La ecuación de la envolvente de las trayectorias se obtiene derivando con respecto a θ o bien, respecto a tanθ e igualando a cero.

$\begin{array}{l} \frac{\partial f}{\partial θ} = 0 \\ 2 \tan θ - 2 \frac{v_{0}^{2}}{g x} = 0 \tan θ = \frac{v_{0}^{2}}{g x} \end{array}$

Combinamos esta ecuación con la de la trayectoria para eliminar el ángulo θ.
F(x,y)=0
Es decir, introducimos la expresión de tanθ en la ecuación de la trayectoria, para obtener la ecuación de la envolvente

$y = - \frac{g}{2 v_{0}^{2}} x^{2} + \frac{v_{0}^{2}}{2 g}$

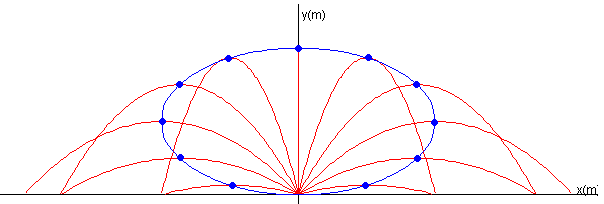
La elipse que une las posiciones de altura máxima

La altura máxima se alcanza cuando v_y=0, en el intante t=v₀·sinθ/g. La posición (x_h, y_h) del proyectil en este instante es

$x_{h} = \frac{v_{0}^{2}}{2 g} sin (2 θ) y_{h} = \frac{v_{0}^{2}}{2 g} {sin}^{2} θ$

Teniendo en cuenta, la relación trigonométrica 1-cos(2θ)=2sin²θ

$x_{h} = \frac{v_{0}^{2}}{2 g} sin (2 θ) y_{h} = \frac{v_{0}^{2}}{4 g} (1 - \cos (2 θ))$

Despejando sin(2θ) en la primera ecuación, cos(2θ), en la segunda, elevando al cuadrado y sumando, eliminamos el ángulo 2θ.

$\frac{x_{h}^{2}}{4 b^{2}} + \frac{{(y_{h} - b)}^{2}}{b^{2}} = 1 b = \frac{v_{0}^{2}}{4 g}$

Esta ecuación representa una elipse centrada en el punto (0, b) cuyos semiejes son 2b y b

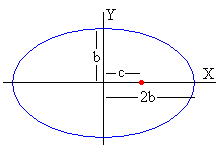La semidistancia focal c y la excentricidad e valen, respectivamente.

$c = \sqrt{4 b^{2} - b^{2}} = b \sqrt{3} e = \frac{c}{2 b} = \frac{\sqrt{3}}{2}$

La excentricidad es un valor constante que no depende de ningún parámetro del movimiento.

Actividades

Se introduce la velocidad inicial de los proyectiles en el control de edición titulado Velocidad inicial.

Se pulsa el botón titulado Empieza

Se representa las trayectorias que siguen los proyectiles disparados con ángulo de tiro θ : 10º, 20º, 30º, 40º, 45º, 50º, 60º, 70º, 80º, 90º.

En la parte superior derecha del applet se muestra el alcance de cada uno de los proyectiles.

El lector puede calcular, el alcance, la altura máxima y el tiempo de vuelo de un proyectil para algunos de los ángulos de tiro especificados y en especial, el que corresponde a 45º, y comparar sus resultados con los proporcionados por el programa interactivo.

CinemaApplet2 aparecerá en un explorador compatible con JDK 1.1.

Referencias

Para el apartado "La elipse que une las posiciones de altura máxima"

Fernández-Chapou J. L., Salas-Brito A. L., Vargas C. A. An elliptic property of parabolic trajectories. Am. J. Phys. 72 (8) August 2004, pp. 1109

Para el apartado "Deducción alternativa de la ecuación de la parábola de seguridad"

Donnelly D. The parabolic envelope of constant initial speed trajectories. Am. J. Phys. 60 (12) December 1992, pp. 1149-1150