Comprobación experimental de la ley de Stefan-Boltzmann
En esta página se va a simular una experiencia que se puede llevar a cabo en el laboratorio para comprobar la ley de Stefan-Boltzmann de la radiación.
De acuerdo con la ley de Stefan-Boltzmann, la energía emitida por un cuerpo negro por unidad de área y por unidad de tiempo es proporcional a la cuata potencia de su temperatura absoluta. La ley de Stefan-Boltzmann es también válida para cualquier otro cuerpo (gris) cuya superficie tenga un coeficiente de absorción (o emitancia) independiente de la longitud de onda.
En el experimento, el cuerpo gris está representado por el filamento incandescente de una lámpara.
Dispositivo experimental
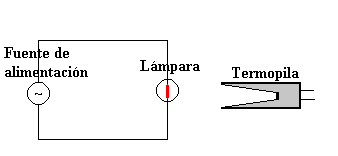 El dispositivo experimental consta de una lámpara incandescente que
produce la radiación, y una termopila de Moll que mide la intensidad de la radiación
producida por la lámpara.
El dispositivo experimental consta de una lámpara incandescente que
produce la radiación, y una termopila de Moll que mide la intensidad de la radiación
producida por la lámpara.
Se conecta una fuente de alimentación alterna a la lámpara. La f.e.m. de la fuente de alimentación se incrementa de voltio en voltio hasta un máximo de 8 voltios. Un amperímetro mide la intensidad de la corriente en el circuito formado por la fuente de alimentación y la resistencia del filamento de la lámpara.
La termopila tiene forma cilíndrica, hueca, que contiene un termopar en su interior. Las paredes interiores son cónicas y plateadas para que reflejen la radiación incidente y la enfoquen en el termopar. La radiación absorbida calienta el termopar produciendo un f.em. termoeléctrica de unos pocos milivoltios.
Descripción
La ley de Stefan-Boltzmann relaciona dos variables: la intensidad emitida por el filamento, y su temperatura absoluta.
- Medida de la intensidad de la radiación emitida por el filamento
La intensidad de la radiación Φ emitida por el filamento es proporcional a la cuarta potencia de su temperatura absoluta T.
Φ =kT4
El flujo de energía (energía por unidad de tiempo) que absorbe la termopila es proporcional a Φ. Ahora bien, la termopila está a la temperatura ambiente T0 y también emite radiación proporcionalmente a la cuarta potencia de T0, de modo que la f.e.m. termoeléctrica Uter vale
donde c es una constante de proporcionalidad desconocida. Podemos despreciar T0 frente a T, de modo que tomando logaritmos neperianos a ambos lados, se cumple que
La representación gráfica de la f.em. termoeléctrica Uter frente a la temperatura absoluta del filamento T en una gráfica doblemente logarítmica conduce a una recta cuya pendiente debe ser próxima a 4.
- Medida de la temperatura T del filamento
La medida de la temperatura del filamento se realiza indirectamente, midiendo su resistencia que varía con la temperatura. Para un filamento de volframio, su resistencia se relaciona con la temperatura de acuerdo con la ecuación
Donde R0 =0.15 Ω , es la resistencia a 0ºC que nos proporciona el fabricante, t es la temperatura en grados centígrados, y los coeficientes α y β, valen para el volframio respectivamente, α =4.82 10-3/K y β =6.76 10-7 /K2
La resistencia del filamento R(t) se calcula aplicando la ley de Ohm, a partir de las indicaciones del voltímetro y del amperímetro.
(1)
La potencia de la lámpara es el producto V·I
Despejando t y teniendo en cuenta que la temperatura absoluta T del filamento es T=t+273, obtenemos
(2)
Actividades
El applet que viene a continuación realiza una práctica demostrativa, con los siguientes datos tomados de la práctica real descrita en el manual citado en las referencias
| Voltímero (V) | Amperímetro (A) | Temperatura del filamento T(K) | Termopila Uter (mV) |
| 1 | 2.20 | 672 | 0.15 |
| 2 | 2.80 | 983 | 0.62 |
| 3 | 3.45 | 1160 | 1.30 |
| 4 | 4.00 | 1300 | 2.20 |
| 5 | 4.45 | 1430 | 3.20 |
| 6 | 4.90 | 1540 | 4.45 |
| 7 | 5.30 | 1630 | 5.90 |
| 8 | 5.70 | 1720 | 7.50 |
Aplicando la fórmula (1) a la primera y segunda columna calculamos la resistencia R(t) del filamento de la lámpara incandescente. Aplicando la fórmula (2) con los datos de R0 =0.15 Ω proporcionado por el fabricante, y los datos de α =4.82 10-3 y β =6.76 10-7 del volframio, obtenemos los valores de la temperatura absoluta del filamento (tercera columna). En la última columna, figuran los datos correspondientes a la lectura de la f.e.m. termoeléctrica Uter.
Pulsando en el botón Nuevo se comienza la experiencia
Pulsando en el botón titulado Siguiente>> se incrementa la f.e.m. de la fuente de alimentación en un voltio.
El amperímetro mide la corriente que pasa por el filamento de la lámpara
El filamento de la lámpara emite luz y cambia de color a medida que se incrementa su temperatura, desde el color negro, pasando por el rojo, hacia el blanco. El número de rayos trazados indica que al aumentar la temperatura aumenta la intensidad de la radiación emitida. Los rayos inciden en la termopila, que muestra el valor de la f.e.m. termoeléctrica. Los valores de la temperatura absoluta del filamento y su correspondiente f.e.m. de la termopila se guardan en un control área de texto, en forma de pares de datos.
Cuando se ha completado la experiencia se pulsa en el botón titulado Gráfica.
Se representan los datos experimentales y la recta que mejor ajusta, en una gráfica doblemente logarítmica. La pendiente de la recta es un valor próximo a 4 tal como nos predice la ley de Stefan-Boltzmann.
Referencias
University Laboratory Experiments. Physics. Volume 4. PHYWE. Pág. 3.17.
