El cuerpo negro. Ejemplos
La lámpara incandescente
La lámpara incandescente se inventó en 1870. La primera lámpara consistía en un filamento de carbón contenida en un recipiente de vidrio en el que se había hecho el vacío. Esta lámpara duraba muy poco y fue sustituida por lámparas de filamento metálico, principalmente de volframio.
La lámpara incandescente funciona cuando un filamento metálico se calienta a altas temperaturas. Los electrones de los átomos emiten energía en todas las longitudes de onda. Cuando una parte importante de la radiación emitida está en el espectro visible y podemos ver el objeto por la radiación visible que emite, decimos que está incandescente.
Para que un sólido emita radiación visible tiene que estar a una temperatura de 850 K, entonces lo vemos de color rojo. Comparando con la temperatura de 6500 K de la fotosfera solar, podemos afirmar que es imposible conseguir calentar un objeto sólido a esta temperatura sin que se funda, para que emita el mismo espectro de la radiación que el Sol.
El volframio es el metal que tiene a la vez la temperatura más alta de fusión 3680 K y el menor grado de evaporación. El carbono soporta temperaturas más elevadas antes de fundirse pero se evapora rápidamente.
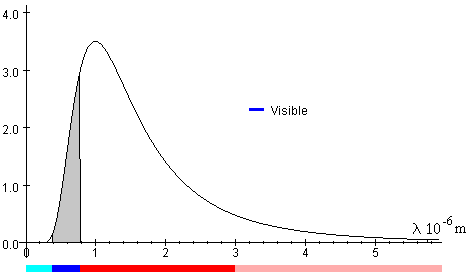
En la práctica, la temperatura más alta que soporta una lámpara incandescente ordinaria fabricada con filamento de volframio es de 2900 K. A estas temperaturas solamente, una pequeña fracción de de la energía emitida está en la región visible, menos del 11%, la mayor parte de es radiación infrarroja. Por lo que las lámparas incandescentes son poco eficientes en la emisión de luz visible.
Hemos supuesto que el filamento se comporta como un cuerpo negro, ignorando la emisividad ε que depende la temperatura y de la longitud de onda y el coeficiente de transmisión del vidrio de la lámpara. Por ejemplo, la emisividad del volframio a la longitud de onda de 0.65·10-6 m (color rojo) y al la temperatura de 2900 K es de ε=0.420.
Actividades
En el applet situado al final de la página anterior
Se introduce
- la temperatura (K), en el control de edición titulado Temperatura
- Elegir en el control de selección titulado Región del espectro, el elemento visible.
Se pulsa el botón titulado Calcular.
Anotar la proporción de la energía emitida por unidad de área y unidad de tiempo en esta región del espectro por un cuerpo negro calentado a esta temperatura.
En la página siguiente se explicará como se determina la temperatura del filamento de una lámpara incandescente a partir de la medida de su resistencia.
La temperatura del Sol
Para determinar la temperatura de la radiación de un cuerpo negro o de una estrella de la misma temperatura se mide la longitud de onda λm a la cual el cuerpo negro emite con intensidad máxima. Aplicando la ley de Wien
λm ·T=2.898·10-3 m·K
se determina la temperatura de dicho cuerpo. Por ejemplo, si el máximo está en la longitud de onda λm=0.5·10-6 m, la temperatura del cuerpo negro es de 5800 K, tal como se muestra en la figura.
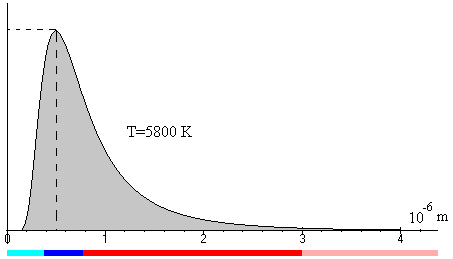
La radiación Sol es absorbida por la atmósfera de la Tierra, por lo que no es fácil determinar la longitud de onda a la cual se produce la máxima intensidad.
Otra forma de medir la temperatura del Sol, es la aplicación de la ley de Stefan-Boltzmann. La energía emitida por unidad de tiempo en todo el espectro por un cuerpo negro a la temperatura T es
P=σAT4
donde A es el área de la superficie del cuerpo. La temperatura T efectiva del Sol será la de un cuerpo negro de la misma área A que emita la energía P por unidad de tiempo del Sol.
Supongamos que el Sol es una esfera de radio R, y que medimos la intensidad de la radiación solar a una distancia r del centro del Sol, por ejemplo en la Tierra.
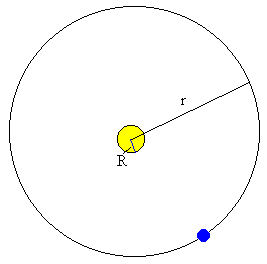 La energía emitida por el Sol, supuesto un cuerpo negro a la temperatura T es
La energía emitida por el Sol, supuesto un cuerpo negro a la temperatura T es
P=4πR2σT4
Si suponemos que el Sol emite en todas las direcciones de forma isótropa. La intensidad de la radicación solar a una distancia r del centro del Sol es
Datos:
- Constante de Stefan-Boltzmann σ =5.67·10-8 (Wm-2K-4).
- Radio del Sol, R=6.96·108 m
- Distancia entre la Tierra y el Sol, r=1.49·1011 m.
- Intensidad de la radiación solar medida en la órbita de la Tierra I=1390 W/m2
Lo que nos da una temperatura T=5790 K o del orden de 6000 K.
Temperatura de un satélite
En este problema se pretende calcular la temperatura de un satélite artificial cuya forma es la de una esfera de radio rs=1 m. Supondremos que la temperatura del satélite es uniforme en toda su superficie y que está en una órbita cercana a la Tierra pero no en su sombra.
- El satélite absorbe en la unidad de tiempo energía procedente del Sol en todas las frecuencias
- En muchas aplicaciones es necesario mantener el satélite tan frío como sea posible. Para enfriar el satélite se utiliza un recubrimiento que refleja la luz por encima de una frecuencia fc tal que hfc/k=1200 K
- Supongamos que el satélite artificial dispone de paneles solares que generan electricidad, la energía generada por los circuitos dentro del satélite actúa como una fuente de calor. Suponiendo que la potencia disipada es de 1000 W, calcular la temperatura final del satélite
Supondremos que el satélite es un cuerpo negro a la temperatura Ts que emite energía por unidad de tiempo al espacio en todas las frecuencias
En el equilibrio, igualando la emisión y absorción de energía, obtenemos
Ts=290 K=17ºC
La intensidad de la radiación absorbida en el intervalo de frecuencias (0, fc) es
Donde la función F(x) se define
Un pequeño programa de ordenador nos proporciona el valor aproximado de F(xc) tomando un número suficientemente grande N pero finito de términos.
tomando N=100 términos, obtenemos F(0.2)=0.9996193
Lo que indica que la energía absorbida es solamente la pequeña proporción δ=1- F(0.2)=3.8066·10-4 de la energía total incidente σT4 en todas las frecuencias.
La energía por unidad de tiempo absorbida por el satélite con el recubrimiento es, por tanto,
Debido al recubrimiento son reflejadas hacia el interior del cuerpo cuya temperatura es Ts las radiaciones de frecuencia comprendida entre 0 a fc
La energía emitida por el cuerpo en la unidad de tiempo será
En el equilibrio, igualamos absorción y emisión
Tomando N=100 términos de la serie, resolvemos la ecuación trascendente para calcular la temperatura Ts del satélite.
Ts=123 K
La energía absorbida más la generada internamente será igual a la energía disipada
La energía generada internamente es muy superior a la energía absorbida procedente del Sol.
Resolviendo la ecuación trascendente obtenemos
Ts=261 K
