El pozo de potencial

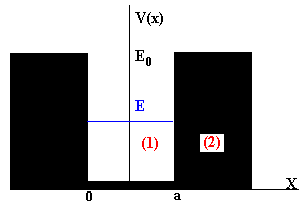
Pozo1.gif (1694 bytes)

Las soluciones de la ecuación de Schrödinger en las regiones (1) y (2) son respectivamente, véase el escalón de potencial (E<E₀).

$\begin{array}{l} Ψ_{1} (x) = A_{1} e^{i q x} + B_{1} e^{- i q x} \\ Ψ_{2} (x) = A_{2} e^{k x} + B_{2} e^{- k x} \\ q^{2} = \frac{2 m E}{ℏ^{2}} k^{2} = \frac{2 m (E_{0} - E)}{ℏ^{2}} \end{array}$

Ψ₂(x) debe tender a cero cuando x se hace grande, para ello A₂ tiene que ser cero.

Las condiciones de continuidad de la función de onda Ψ(x) y su derivada primera en la frontera x=a entre las dos regiones de distinto potencial, constituyen un par de ecuaciones que relacionan A₁ y B₁ con B₂.

Este último parámetro, determina la escala vertical de la función de onda Ψ(x), y se puede obtener a partir de la condición de normalización

$\int_{- \infty}^{+ \infty} {| Ψ (x) |}^{2} d x = 1$

La simetría de la función potencial E_p(x) hace que los estados de energía de la partícula puedan ser

Simétricos si Ψ(x)=Ψ(- x)
Antisimétricos si Ψ(x)=-Ψ(-x)

Los niveles de energía para los estados simétricos se determinan haciendo Ψ(x)=Ψ(-x). Operando y simplificando se obtiene la ecuación trascendente de la energía

q·sin(qa)-k·cos(qa)=0

Los niveles de energía para los estados antisimétricos se obtienen haciendo Ψ(x)=-Ψ(-x). Se obtiene la ecuación

k·sin(qa)+q·cos(qa)=0

Las raíces de las dos ecuaciones nos dan los niveles de energía de la partícula en el pozo de potencial. Dichas raíces se calculan empleando el procedimiento del punto medio. En el applet que viene a continuación se calcula los niveles de energía y se representa las funciones de onda de un pozo de potencial de altura y anchura dadas.

Actividades

Se introduce

la anchura del pozo de potencial, en el control de edición titulado Anchura
la altura del pozo de potencial, en el control de edición titulado Altura

Se pulsa en el botón titulado Gráfica, para observar los primeros niveles de energía y la representación de sus funciones de onda.

Comparar las funciones de onda de los primeros niveles con sus correspondientes de una caja de potencial.

Observar que los niveles de energía se suceden de menor a mayor del siguiente modo: el nivel fundamental o de más baja energía tiene paridad par (la función de onda es simétrica), a continuación viene un nivel de energía de paridad impar (la función de onda es antisimétrica), seguido de un nivel de paridad par, y así sucesivamente,...

Búsqueda de los niveles de energía

En general, los niveles de energía de una partícula de masa m, confinada en una región unidimensional en la que existe un potencial E_p(x) viene dada por la solución de la ecuación de Schrödinger independiente del tiempo.

$\frac{- ℏ^{2}}{2 m} \frac{d^{2} Ψ}{d x^{2}} + E_{p} (x) Ψ = E Ψ$

Con las condiciones de contorno

$\lim_{x \to \pm \infty} Ψ (x) = 0$

Es decir, E es la energía de un nivel, si la solución de le ecuación de Schrödinger, Ψ(x) tiende asintóticamente a cero para grandes valores de x.

En el applet que viene a continuación, vamos a buscar los niveles de energía de un sistema mecánico-cuántico simple, un pozo de potencial, que consiste en una región de anchura a y de altura E₀

Para ello, no se precisará resolver ninguna ecuaciones transcendente de la energía. Seguiremos el procedimiento de prueba y error, ensayando con valores de la energía hasta encontrar aquél en el que la solución de la ecuación de Schrödinger tienda asintóticamente a cero cuando x se hace grande.

La búsqueda no se realizará al azar, sino que estará guiada por la siguiente estrategia que conducirá rápidamente a encontrar la solución aproximada:

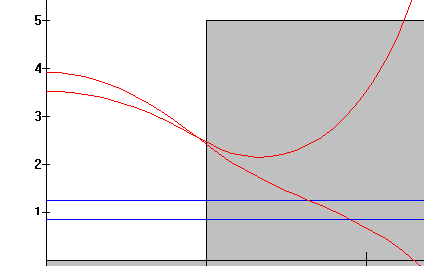
Pozo2.gif (2617 bytes)

El nivel de energía estará comprendido entre dos valores próximos para los cuales la solución de la ecuación de Schrödinger diverge positivamente y negativamente, respectivamente.

Si para las energías de prueba, ocurre que

$\begin{array}{l} E_{1} \to \lim_{x \to \infty} Ψ (x) = + \infty \\ E_{2} \to \lim_{x \to \infty} Ψ (x) = - \infty \end{array}$

El nivel de energía buscado estará comprendido entre E₁ y E₂. Disminuyendo el intervalo (E₁, E₂) encontraremos el nivel de energía dentro de la precisión requerida.

Ejemplo:

Sea un pozo de potencial de 2 unidades de anchura y 5 de altura. Buscamos los niveles de energía que corresponden a funciones de onda de paridad par. Para la energía E₁=0.85 la solución de la ecuación de Schrödinger diverge positivamente y para E₂=1.25 diverge negativamente. Por tanto, hemos localizado el intervalo (0.85, 1.25) donde existe un nivel de energía. Disminuyendo progresivamente el intervalo, encontraremos el nivel de energía dentro de la precisión requerida en el valor 1.15.

Actividades

Se introduce

la anchura del pozo de potencial, en el control de edición titulado Anchura
la altura del pozo de potencial, en el control de edición titulado Altura

Se pulsa el botón titulado Nuevo. Se representa medio pozo de potencial.

Se selecciona el botón de radio titulado Par, que indica que vamos a buscar primero los niveles de energía cuyas funciones de onda sean simétricas.

Ensayar un valor de la energía, introduciendo en el control de edición titulado Energía. Este valor, naturalmente, no puede ser cero, ni mayor que la altura del pozo de potencial.

Pulsar el botón Hallar, para que se represente la solución de la ecuación de Schrödinger para esta energía.

Probar con otro valor de la energía y así sucesivamente, siguiendo la estrategia comentada anteriormente, hasta encontrar aquél valor que hace que la solución de la ecuación de Schrödinger tienda a cero cuando x se hace grande, es decir, tenga como asíntota horizontal la recta que señala el nivel de energía.

Pulsar el botón Guardar, para guardar el valor del nivel de energía y su paridad en control lista titulado Niveles hallados.

Cuando se acumulen muchas funciones de onda en la ventana se puede limpiar el área de trabajo pulsando en el botón Borrar.

Si guardamos en la caja de listas un valor equivocado, podemos suprimirlo seleccionado dicho valor con el ratón y pulsando en el botón titulado Eliminar.

Para buscar los niveles de forma ordenada, se habrá observado que el estado fundamental, el de menor energía, corresponde a un estado simétrico. Los estados se suceden al incrementarse la energía alternadamente, es decir, a un estado cuya función de onda es de paridad par le sucede otro cuya función de onda es de paridad impar, a continuación viene otro de paridad par, y así sucesivamente.

Comprobaremos que hemos encontrado todos los niveles, retornando al apartado anterior para obtener la representación de todos niveles de energía, y de sus correspondientes funciones de onda.