SiguienteAnterior

Trayectoria circular y parabólica

  1. La partícula describe una trayectoria circular si la velocidad en la parte más baja del bucle es

v 0 ≥ 5Rg

  1. La partícula se mueve hacia atrás cuando

v 0 ≤ 2Rg

  1. Cuando la velocidad v0 está comprendida entre estos dos valores, la partícula describe una trayectoria circular y a continuación, una trayectoria parabólica. En la trayectoria circular la distancia entre la partícula y el centro es R, en la trayectoria parabólica la distancia entre la partícula y el centro es menor que R.

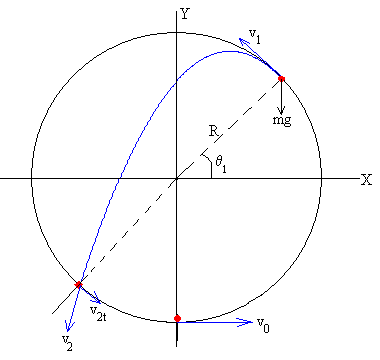
Para analizar este movimiento complejo, situamos el origen en el centro de la trayectoria circular y medimos los ángulos desde el eje X. El nivel cero de energía potencial lo situamos en el eje X.

En la posición angular θ1 la partícula deja de describir la trayectoria circular, la tensión T de la cuerda es nula. En este momento, la ecuación de la dinámica del movimiento circular y el principio de conservación de la energía se escriben

mgsin⁡ θ 1 =m v 1 2 R 1 2 m v 0 2 −mgR= 1 2 m v 1 2 +mgRsin⁡ θ 1

Combinando ambas ecuaciones determinamos el valor del ángulo θ1

v 0 2 =2gR+3gRsin⁡ θ 1

Una vez que llega P1 describe un movimiento parabólico, la velocidad y la posición de la partícula es

{ v x =− v 1 sin⁡ θ 1 v y = v 1 cos⁡ θ 1 −gt   { x=Rcos⁡ θ 1 − v 1 sin⁡ θ 1 t y=Rsin⁡ θ 1 + v 1 cos⁡ θ 1 t− 1 2 g t 2

En el punto P2 la distancia entre la partícula y el centro vuelve a ser R. P2  es el punto de intersección entre la parábola y la circunferencia de radio R. Recordando que la ecuación de una circunferencia, cuando su centro está en el origen de coordenadas es

x 2 + y 2 = R 2 ( Rcos⁡ θ 1 − v 1 sin⁡ θ 1 t ) 2 + ( Rsin⁡ θ 1 + v 1 cos⁡ θ 1 t− 1 2 g t 2 ) 2 = R 2

Teniendo en cuenta que de la dinámica del movimiento circular

v 1 2 =Rgsin⁡ θ 1

Llegamos a la siguiente expresión simplificada

t 3 g( 1 4 gt− v 1 cos⁡ θ 1 )=0

El tiempo de vuelo de la partícula hasta que choca con el bucle es

t= 4 v 1 cos⁡ θ 1 g

La posición del punto P2 y la velocidad de la partícula son, respectivamente

{ v 2x =− v 1 sin⁡ θ 1 v 2y =−3 v 1 cos⁡ θ 1  { x 2 =Rcos⁡ θ 1 − 4 v 1 2 sin⁡ θ 1 cos⁡ θ 1 g =−3Rcos⁡ θ 1 +4R cos 3 θ 1 y 2 =Rsin⁡ θ 1 − 4 v 1 2 cos⁡ 2 θ 1 g =Rsin⁡ θ 1 −4Rsin⁡ θ 1 cos 2 θ 1

Supondremos que cuando la cuerda se estira al máximo, se anula la componente normal de la velocidad y la partícula describe de nuevo una trayectoria circular con la componente tangencial de dicha velocidad como velocidad inicial.

La componente normal de la velocidad se calcula mediante el producto escalar r2·v2

v 2r = r 2 · v 2 R    v 2t 2 = v 2 2 − v 2r 2

El módulo del vector posición r2 del punto P2 es el radio R de la circunferencia

v 2r =8 v 1 sin⁡ θ 1 cos 3 θ 1 v 2t 2 = v 1 2 (1+8 cos 2 θ 1 −64 cos 6 θ 1 +64 cos 8 θ 1 ) v 2t = v 1 (1+4 cos 2 θ 1 −8 cos 4 θ 1 )

La energía final de la partícula en el punto P2 final de la trayectoria parabólica es

E 2 = 1 2 m v 2t 2 +mg y 2 =mgRsin⁡ θ 1 ( 1 2 −32 cos⁡ 6 θ 1 +32 cos⁡ 8 θ 1 )

Esta energía es menor que la energía de la partícula en el punto de lanzamiento

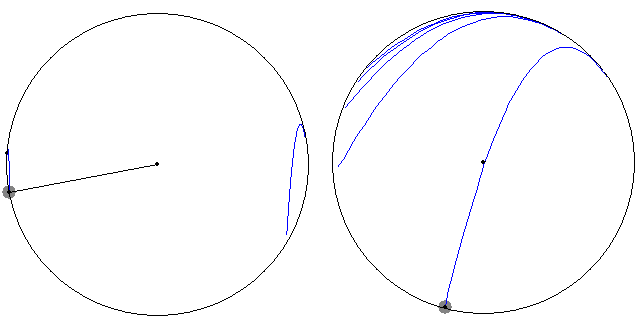
E= 1 2 m v 0 2 −mgR= 1 2 m v 1 2 +mgRsin⁡ θ 1 = 3 2 mgRsin⁡ θ 1

En la figura, se muestran las trayectorias parabólicas seguidas por la partícula. En la figura de la izquierda las parábolas se producen a la derecha y a la izquierda. Las parábolas son cada vez más pequeñas por que la partícula va perdiendo energía, esta pérdida se produce cuando se finaliza la trayectoria parabólica y la cuerda se estira al máximo.

En la figura de la derecha, tenemos una sucesión de cinco trayectorias parabólicas, hasta que la partícula casi se detiene al final de la última trayectoria.

SiguienteAnterior