El péndulo balístico (I)

Se dispara horizontalmente una bala contra un bloque suspendido de una cuerda. Este dispositivo se denomina péndulo balístico y se usa para determinar la velocidad de la bala midiendo el ángulo que se desvía el péndulo después de que la bala se haya incrustado en él. Supondremos que el bloque es una masa puntual suspendido de una cuerda inextensible y sin peso. En el capítulo Sólido rígido, estudiaremos una segunda versión del péndulo balístico en el que la cuerda es sustituida por una varilla rígida y el bloque por un cilindro.

Descripción

De la conservación del momento lineal obtenemos la velocidad v_B inmediatamente después del choque del sistema formado por el péndulo y la bala incrustada en él.

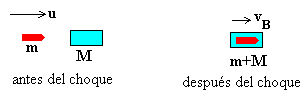
Si M es la masa del bloque, m la masa de la bala y u su velocidad, dicho principio se escribe

mu=(m+M)v_B

Después de la colisión pueden ocurrir los siguientes casos, (véase el bucle) dependiendo del valor de la energía cinética adquirida por el sistema formado por el péndulo y la bala incrustada en él.

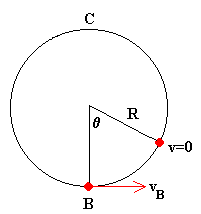
choques6.gif (1128 bytes)

Que el ángulo máximo de desviación del péndulo no supere los 90º

La conservación de la energía se escribe

$\frac{1}{2} (m + M) v_{B}^{2} = (m + M) g R (1 - \cos θ)$

Midiendo el ángulo θ obtenemos v_B y de la conservación del momento lineal obtenemos la velocidad de la bala u.

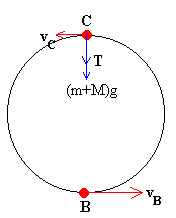
choques7.gif (1122 bytes)

Que el péndulo dé vueltas

$\frac{1}{2} (m + M) v_{B}^{2} = \frac{1}{2} (m + M) v_{C}^{2} + 2 (m + M) g R$

Ahora bien, la velocidad en el punto más alto C debe superar un valor mínimo.

De las ecuaciones de la dinámica del movimiento circular tenemos que

$(m + M) g + T = (m + M) \frac{v_{C}^{2}}{R}$

Siendo T la tensión de la cuerda. La velocidad mínima se obtiene cuando T=0,

$v_{C m í n} = \sqrt{R g}$ . Entonces $v_{B}^{2} = 5 g R$

Que el péndulo se desvíe un ángulo comprendido entre 90º y 180º

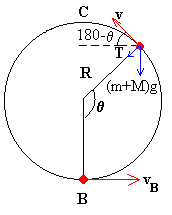choques8.gif (1230 bytes) De la dinámica del movimiento circular y el principio de conservación de la energía tenemos que

$\begin{array}{l} T + (m + M) g \cos (180 - θ) = (m + M) \frac{v^{2}}{R} \\ \frac{1}{2} (m + M) v_{B}^{2} = \frac{1}{2} (m + M) v^{2} + (m + M) g R (1 + \cos (180 - θ)) \end{array}$

La cuerda del péndulo deja de tener efecto en el instante en el que su tensión es cero T=0. Por lo que

$v_{B}^{2} = g R (2 - 3 \cos θ) θ > 90$

En dicho instante, la partícula se mueve bajo la única fuerza de su propio peso describiendo un movimiento curvilíneo bajo la aceleración constante de la gravedad o un tiro parabólico

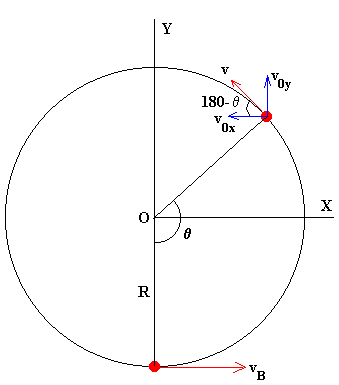
En dicho instante, la partícula se mueve bajo la única fuerza de su propio peso describiendo un movimiento curvilíneo bajo la aceleración constante de la gravedad o un tiro parabólico

$\begin{array}{l} v_{0 x} = v \cos (180 - θ) v_{0 y} = v \sin (180 - θ) \\ x = R \sin (180 - θ) - v_{0 x} t y = R \cos (180 - θ) + v_{0 y} t - \frac{1}{2} g t^{2} \end{array}$

Tomando el centro del bucle como origen de coordenadas. El péndulo vuelve a oscilar cuando se cumpla que $x^{2} + y^{2} = R^{2}$

Un estudio de tallado de la interesante combinación de movimiento circular y parabólico se encuentra en la sección, más abajo, "Trayectoria circular y parabólica". Véase también el ejemplo análogo del movimiento de una partícula en un bucle.

Ejemplo1

Velocidad de la bala, u=10 m/s
Masa de la bala, m=0.2 kg
Masa del bloque, M=1.5 kg
La longitud del péndulo es R=0.5 m

La velocidad v_B del conjunto formado por la bala y el bloque inmediatamente después del choque, es

m·u=(m+M)v_B, v_B=1.18 m/s

Aplicamos el principio de conservación de la energía para calcula la máxima desviación del péndulo

$\frac{1}{2} (m + M) v_{B}^{2} = (m + M) g h h = R - R \cos θ$

Conocido v_B despejamos h=0.07 m, y calculamos el ángulo θ=30.8º

Ejemplo 2

¿Cuál debe ser la velocidad mínima u de la bala para que el péndulo describa una circunferencia?.

Masa de la bala, m=0.2 kg
Masa del bloque, M=1.5 kg
La longitud del péndulo es R=0.5 m

Calculamos la velocidad mínima v_C de la partícula en el punto más alto de la trayectoria circular, cuando la tensión de la cuerda es cero, aplicando la ecuación de la dinámica del movimiento circular uniforme.

$v_{C} = \sqrt{9.8 \cdot 0.5} = 2.21 m/s$

Aplicando el principio de conservación de la energía, calculamos la velocidad de la partícula en el punto B más bajo de la trayectoria circular.

$\frac{1}{2} (m + M) v_{B}^{2} = \frac{1}{2} (m + M) v_{C}^{2} + (m + M) g \cdot 2 R v_{B} = 4.95 m/s$

Aplicamos el principio de conservación del momento lineal, para calcular la velocidad de la bala u antes del choque

m·u=(M+m)v_B, u=42.07 m/s

Ejemplo 3

Velocidad de la bala, u=35 m/s
Masa de la bala, m=0.2 kg
Masa del bloque, M=1.5 kg
La longitud del péndulo es R=0.5 m

La velocidad v_B del conjunto formado por la bala y el bloque inmediatamente después del choque, es

m·u=(m+M)v_B, v_B=4.12 m/s

Aplicamos el principio de conservación de la energía, para calcular la máxima desviación del péndulo

$\frac{1}{2} (m + M) v_{B}^{2} = (m + M) g h h = R - R \cos θ$

Conocido v_B despejamos h=0.87 m, que es mayor que la longitud R=0.5 del péndulo

La cuerda del péndulo deja de tener efecto en el instante en el que su tensión es cero T=0. Por lo que

$\begin{array}{l} (m + M) g \cos (180 - θ) = (m + M) \frac{v^{2}}{R} \\ \frac{1}{2} (m + M) v_{B}^{2} = \frac{1}{2} (m + M) v^{2} + (m + M) g R (1 + \cos (180 - θ)) \end{array}$

En este sistema de ecuaciones, calculamos el ángulo θ=119.1º y la velocidad de la partícula v=1.54 m/s

El movimiento posterior de la partícula viene descrito por las siguientes ecuaciones del tiro parabólico.

$\begin{array}{l} v_{0 x} = v \cos (180 - θ) = 0.75 m/s v_{0 y} = v \sin (180 - θ) = 1.35 m/s \\ x = 0.44 - 0.75 \cdot t y = 0.24 + 1.35 \cdot t - 4.9 \cdot t^{2} \end{array}$

Actividades

Se introduce

La masa de la bala en kg, en el control de edición titulado Masa de la bala
La velocidad de la bala en m/s, en el control de edición titulado Velocidad de la bala
La masa del bloque que pende de la cuerda en kg, en el control de edición titulado Masa bloque.
Dato: la longitud del péndulo es de 0.5 m

Se pulsa el botón titulado Empieza.

Se observa el movimiento del péndulo. Se representa la energía del sistema después del choque.

Se modifica la masa del bloque de modo que se pueda medir la desviación del péndulo en la escala graduada.

Se recomienda al lector que obtenga el valor de la desviación del péndulo para valores dados de la masa de la bala, velocidad de la bala y masa del bloque, y compruebe la solución obtenida con la proporcionada por el programa interactivo.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.