• Inicio
• Dinámica
• Movimiento circular uniforme

Un cuerpo se lanza hacia "arriba" desde el “suelo” de la nave espacial en movimiento de rotación

Sea una nave cilíndrica de radio R, que gira alrededor de su eje con velocidad angular constante ω.

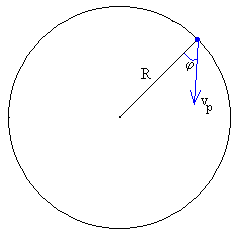Sistema de Referencia de la Nave espacial

Se lanza un objeto mediante un dispositivo situado en el “suelo” de la nave con una velocidad v_p haciendo un ángulo φ con la dirección radial tal como se muestra en la figura.

Este objeto puede ser una pelota que lanza un astronauta desde el “suelo” de la nave espacial.

Sistema de Referencia Inercial

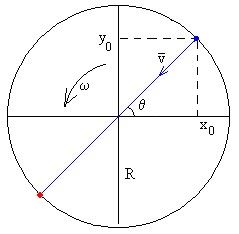
Desde el punto de vista del observador inercial, la velocidad del objeto v es la suma vectorial v=v_p+v_n  donde v_n es la velocidad del dispositivo, cuya dirección es tangencial y cuyo módulo es v_n=ωR

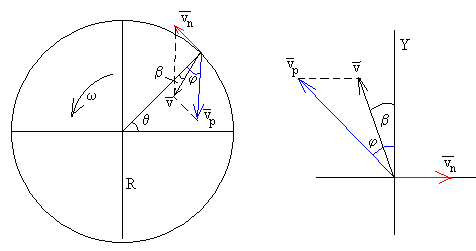
El módulo v del vector resultante y el ángulo β que forma con la dirección radial Y es

${\displaystyle \begin{array}{l}\tan \beta =\frac{v_p\sin \varphi -v_n}{v_p\text{cos}\varphi }\\ v=\sqrt{v_p^2+v_n^2-2v_p{v}_n\sin \varphi }\end{array}}$

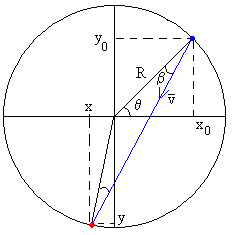El objeto es lanzado desde la posición x₀, y₀ en el instante t=0

x₀=R·cosθ
y₀=R·sinθ

describe un movimiento rectilíneo y uniforme.

x= R·cosθ-v·cos(θ+β)·t
y= R·sinθ-v·sin(θ+β)·t

La trayectoria es la cuerda que une el punto de lanzamiento (x₀, y₀) y el punto (x, y) de impacto en el “suelo” de la nave espacial. El punto de lanzamiento, el centro de la circunferencia y el punto de impacto, forman un triángulo isósceles. La distancia entre el punto de lanzamiento y de impacto es 2Rcosβ, y el tiempo  t de vuelo es

${\displaystyle t=\frac{2R\cos \beta }{v}}$

Tirando hacia "arriba" en dirección radial

Sistema de Referencia Inercial

Cuando el objeto sigue la dirección radial β=0 (hacia “arriba”) es posible que impacte en el dispositivo que lo lanzó. Por ejemplo, si un astronauta lanza una pelota hacia “arriba”, es posible que el mismo astronauta la recoja con la mano.

Para ello, se tiene que cumplir que el tiempo que tarda el objeto en atravesar la nave espacial

${\displaystyle t=\frac{2R}{v}}$

sea igual al tiempo que emplea el dispositivo lanzador en girar π radianes ó180º

${\displaystyle t=\frac{\pi }{\omega }}$

El objeto deberá atravesar la nave espacial en dirección radial, con una velocidad v dada por

${\displaystyle v=\frac{2R\omega }{\pi }}$

Sistema de Referencia de la Nave espacial

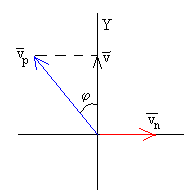El ángulo de tiro φ, medido respecto de la dirección radial y la velocidad v_p con la que se tiene que lanzar el objeto, se calculan resolviendo el triángulo rectángulo de la figura.

${\displaystyle \begin{array}{l}\tan \varphi =\frac{\omega R}{v}=\frac{\pi }{2}\varphi =57.5º\\ v_p=\sqrt{v^2+{\omega }^2{R}^2}\end{array}}$

En general, para que el objeto impacte en el dispositivo lanzador, el tiempo que tarda el objeto en atravesar la nave espacial t=2R/v deberá ser igual al tiempo que tarda el dispositivo en girar 1½, 2½,… n+½ vueltas

${\displaystyle t=\frac{\left(n+\frac{1}{2}\right)2\pi }{\omega }v=\frac{R\omega }{\left(n+\frac{1}{2}\right)\pi }}$

El ángulo de tiro y la velocidad de lanzamiento del objeto v_p serán

${\displaystyle \begin{array}{l}\tan \varphi =\frac{R\omega }{v}=\left(n+\frac{1}{2}\right)\pi \\ v_p=\sqrt{v^2+{\omega }^2{R}^2}\end{array}}$

A medida que n aumenta, φ se aproxima a π/2, y v tiende a cero. El objeto permanecerá en reposo para un observador inercial. Por ejemplo, el astronauta se encontrará con la pelota después de dar una vuelta completa.

Ejemplo:

• Radio de la nave espacial R=10 m

• Velocidad angular de giro ω=1 rad/s

1. Cuando el dispositivo lanzador gira n=0, media vuelta después de haber lanzado el objeto.

El ángulo de tiro ya se ha calculado, φ=57.5º

${\displaystyle \begin{array}{l}{v}_n=\omega R=10\text{m/s }v=\frac{20}{\pi }\text{m/s}\\ v_p=\sqrt{\frac{{20}^2}{{\pi }^2}+{10}^2}=11.85\text{m/s}\end{array}}$

1. Cuando n=1, el dispositivo lanzador gira vuelta y media después de haber lanzado el objeto.

${\displaystyle \begin{array}{l}\tan \varphi =\frac{3\pi }{2}\varphi =\text{78}\text{.0º}\\ v_p=\sqrt{\frac{{20}^2}{3^2{\pi }^2}+{10}^2}{v}_p=10.22\text{m/s}\end{array}}$

Tiro oblicuo

Sistema de Referencia Inercial

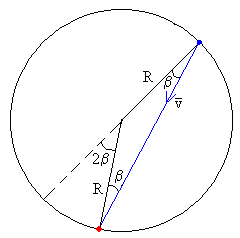Como vemos en la figura, para que el objeto impacte en el dispositivo lanzador, se tiene que cumplir que el tiempo que invierte el objeto en recorrer la cuerda que une el punto de lanzamiento y de impacto sea igual al que invierte el lanzador en recorrer el arco de ángulo π+2β.

${\displaystyle \frac{2R\cos \beta }{v}=\frac{\pi +2\beta }{\omega }v=\frac{2\omega R\cos \beta }{\pi +2\beta }}$

o bien, en general

${\displaystyle v=\frac{2\omega R\cos \beta }{\left(n+\frac{1}{2}\right)2\pi +2\beta }n=\text{0}\text{, 1}\text{, 2}\mathrm{...}}$

 

Sistema de Referencia de la Nave espacial

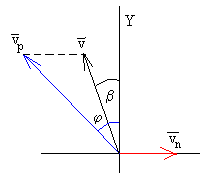La velocidad de lanzamiento v_p y el ángulo de tiro φ medido respecto de la dirección radial se calculan hallando la diferencia de vectores v_p=v-v_n

${\displaystyle \begin{array}{l}\tan \varphi =\frac{v\sin \beta +v_n}{v\text{cos}\beta }\\ v_p=\sqrt{v^2+v_n^2+2v{v}_n\sin \beta }\end{array}}$

 

 

Ejemplo:

• Lanzamiento respecto al Sistema de Referencia Inercial

Sea β=30º

Para que el objeto impacte en el dispositivo lanzador al completar algo más de media vuelta n=0, la velocidad v deberá ser

${\displaystyle v=\frac{2·1·10·\cos 30}{\pi +2·\pi /6}=\text{4}\text{.14}\text{m/s }}$

• Lanzamiento respecto del Sistema de Referencia de la Nave espacial

${\displaystyle \begin{array}{l}\tan \varphi =\frac{4.14·\sin \text{30}+1·10}{4.14·\text{cos30}}\varphi =73.5º\\ v_p=\sqrt{{4.14}^2+{10}^2+2·4.14·10·\sin \text{30}}=12.59\text{m/s}\end{array}}$

Actividades

Se pulsa el botón titulado Inicio

Se introduce

• La velocidad de lanzamiento v_p del objeto desde el "suelo" de la nave espacial, actuando en la barra de desplazamiento o en el control de edición titulado Velocidad.

• El ángulo φ que forma la dirección de dicha velocidad con la dirección "vertical" (o radial) actuando en la barra de desplazamiento o en el control de edición titulado Ángulo

• El radio R de la nave espacial se ha fijado en R=10 m

• La velocidad angular de rotación se ha fijado en ω=1 rad/s

Se pulsa el botón titulado Empieza

• El dispositivo lanzador, se representa mediante un pequeño círculo de color azul

• El objeto lanzado, se representa mediante un círculo más pequeño de color rojo.

Se observa el movimiento del objeto lanzado, y se representa la trayectoria rectilínea que sigue, mientras atraviesa la nave, hasta que impacta en el "suelo"

Fijada la velocidad de lanzamiento v_p, cambiaremos el ángulo de tiro φ hasta conseguir que el objeto impacte en el dispositivo lanzador.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Fisher N. Space science 2001: some problems with artificial gravity. Physics Education 36 (3) May 2001, pp. 193-201

Paetkau M., Tossing on a rotating space station. The Physics Teacher, 42, October 2004, pp. 423-426

Curso Interactivo de Física en Internet © Ángel Franco García