Medida del coeficiente de rozamiento por deslizamiento (II)

En esta página, se simula otra experiencia que nos permite medir el coeficiente de rozamiento por deslizamiento.

Consideremos dos bloques A y B unidos por una cuerda inextensible que pasa por una polea de masa despreciable. Cuando el bloque A desciende una altura h es detenido por una placa y la cuerda deja de tirar del bloque B. El bloque B desliza a lo largo del plano horizontal hasta que se detiene después de desplazarse una distancia x.

Descripción

El problema tiene dos partes:

Movimiento del sistema formado por los dos bloques unidos por una cuerda

En la figura, se representan las fuerzas sobre cada unos de los bloques (en color azul) y la aceleración (en color rojo).

Sobre el cuerpo A de masa m_A actúan dos fuerzas

El peso m_Ag
La tensión de la cuerda T.

Sobre el bloque B actúan cuatro fuerzas

El peso m_Bg
La tensión de la cuerda T.
La reacción del plano horizontal N=m_Bg
La fuerza de rozamiento F_r=μ_k·N

La ecuación del movimiento del bloque A es

m_A·g-T=m_A·a

La ecuación del movimiento del bloque B es

T -F_r=m_B·a

Despejando la aceleración a en el sistema de dos ecuaciones

$a = \frac{m_{A} - μ_{k} m_{B}}{m_{A} + m_{B}} g$

La velocidad que alcanza después de desplazarse h, partiendo del reposo es

$v^{2} = 2 \frac{m_{A} - μ_{k} m_{B}}{m_{A} + m_{B}} g h$

Movimiento del bloque B sobre el plano horizontal

La cuerda deja de tirar del bloque B cuando pasa por la posición señalada por O.

El bloque B se detiene después de desplazarse x.

Las fuerzas que actúan sobre el bloque B son

El peso m_B·g
La reacción del plano horizontal N=m_B·g
La fuerza de rozamiento F_r=μ_k·N

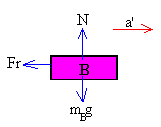La ecuación del movimiento es

F_r=m_B·a’

a’= -μ_kg

De las ecuaciones del movimiento rectilíneo uniformemente acelerado, tenemos

$\begin{array}{l} 0 = v - μ_{k} g \cdot t \\ x = v t - \frac{1}{2} μ_{k} g \cdot t^{2} \end{array}$

Eliminando el tiempo t

$x = \frac{1}{2} \frac{v^{2}}{μ_{k} g} = \frac{m_{A} - μ_{k} m_{B}}{m_{A} + m_{B}} \frac{h}{μ_{k}}$

Conocidos x y h y los valores de las masas m_A y m_B se puede determinar el coeficiente de rozamiento cinético μ_k.

$μ_{k} = \frac{m_{A} h}{(m_{A} + m_{B}) x + m_{B} h}$

Cuando las masas son iguales m_A=m_B para determinar el coeficiente μ_k solamente es necesario medir las distancias h y x.

$μ_{k} = \frac{h}{h + 2 x}$

Ejemplo

Masa del bloque B, m_B=2.5 kg.
Masa del bloque A, m_A=6.3 kg.
El desplazamiento h=1.0 m
El desplazamiento del bloque B después de dejar de actuar la cuerda es x=0.75 m

$μ_{k} = \frac{m_{A} h}{(m_{A} + m_{B}) x + m_{B} h} = \frac{6.3 \cdot 1.0}{(6.3 + 2.5) \cdot 0.75 + 2.5 \cdot 1.0} = 0.692$

Comprobación:

Calculamos la aceleración del sistema formado por el bloque A y el bloque B unidos por una cuerda

$a = \frac{m_{A} - μ_{k} m_{B}}{m_{A} + m_{B}} g = \frac{6.3 - 0.692 \cdot 2.5}{6.3 + 2.5} 9.8 = 5.09 {m/s}^{2}$

La velocidad del bloque B cuando pasa por O, en el instante en el que deja de actuar la cuerda es v=3.19 m/s empleando un tiempo de t=0.63 s.

Tenemos ahora, un bloque con velocidad inicial de v=3.19 m/s que desliza a lo largo de un plano horizontal con rozamiento, es decir, con una aceleración a’= -μ_kg=-0.692·9.8=-6.78 m/s² de sentido contrario a la velocidad.

El tiempo que tarda en parase es t=0.47 s, y se desplaza x=0.75 m

El desplazamiento total del bloque B es de 1.75 m y el tiempo que tarda en desplazarse es de 0.63+0.47=1.10 s.

Actividades

Se pulsa el botón titulado Nuevo, y el programa interactivo genera de forma aleatoria el valor del coeficiente de rozamiento cinético entre el cuerpo B y el plano horizontal.

Se introduce

La masa del bloque A, en el control de edición titulado Masa A
La masa del bloque B está fijada en el programa interactivo en 2.5 kg
El desplazamiento h inicial del bloque B, mientras acelera, en 1 m

Se pulsa el botón Empieza.

Se mide el desplazamiento x del bloque a partir del origen O, es decir, a partir del momento en el que deja de actuar la cuerda. Se calcula el coeficiente de rozamiento cinético.

Se pulsa el botón titulado Respuesta, para comparar nuestros resultados con los proporcionados por el programa interactivo.

Activando la casilla titulada Vectores, se representan las fuerzas que actúan sobre el bloque B.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Eagleson H. V., An experimental method for determining coefficients of sliding friction. Am. J. Phys. 13 (1945), pp. 43-44

Reidl C. The coefficient of kinetic friction. The Physics Teacher. September 1990, pp. 40