El rozamiento por deslizamiento

Comportamiento de un cuerpo que descansa sobre un plano horizontal

Dibujemos una gráfica en la que en el eje horizontal representamos la fuerza F aplicada sobre el bloque y en el eje vertical la fuerza de rozamiento.

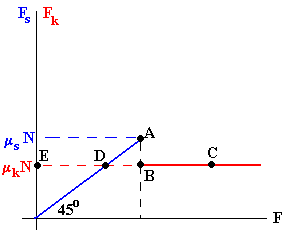
Desde el origen hasta el punto A la fuerza F aplicada sobre el bloque no es suficientemente grande como para moverlo. Estamos en una situación de equilibrio estático

F= F_s<μ_sN

En el punto A, la fuerza de rozamiento estático F_s alcanza su máximo valor μ_sN

F= F_{s máx}=μ_sN

Si la fuerza F aplicada se incrementa un poquito más, el bloque comienza a moverse. La fuerza de rozamiento disminuye rápidamente a un valor menor e igual a la fuerza de rozamiento por deslizamiento, F_k=μ_kN

Si la fuerza F no cambia, punto B, y permanece igual a F_{s máx} el bloque comienza moviéndose con una aceleración

a=(F-F_k)/m

Si incrementamos la fuerza F, punto C, la fuerza neta sobre el bloque F-F_k se incrementa y también se incrementa la aceleración.

En el punto D, la fuerza F aplicada es igual a F_k por lo que la fuerza neta sobre el bloque será cero. El bloque se mueve con velocidad constante.

En el punto E, se anula la fuerza aplicada F, la fuerza que actúa sobre el bloque es - F_k, la aceleración es negativa y la velocidad decrece hasta que el bloque se para.

Experiencia

Un bloque de masa m descansa sobre un plano horizontal, el bloque está unido mediante un hilo inextensible y de peso despreciable que pasa por una polea a un platillo sobre el que se depositan pesas. Vamos a estudiar el comportamiento del bloque y a realizar medidas del coeficiente estático y cinético.

Medida del coeficiente estático

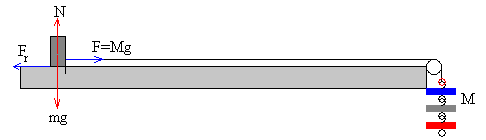
Se van colocando pesas en el platillo y el bloque permanece en reposo. La fuerza de rozamiento vale

F_r=Mg

donde M es la masa de las pesas que contiene el platillo

Cuando va a empezar a deslizar, la fuerza de rozamiento F_r adquiere el valor máximo posible μ_sN=μ_smg

$μ_{s} = \frac{M}{m}$

Medida del coeficiente cinético

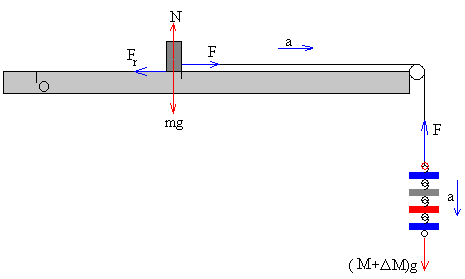
Añadimos una pesa más ΔM y el bloque empieza a deslizar, desplazándose una longitud x en un t. La aceleración es

$x = \frac{1}{2} a t^{2}$

Aplicamos la segunda ley de Newton al movimiento del bloque

F-F_r=ma
F_r=μ_k·N
N=mg

Aplicamos la segunda ley de Newton al movimiento del platillo y las pesas

(M+ΔM)g-F=(M+ΔM)a

Despejamos el coeficiente cinético μ_k

$μ_{k} = \frac{(M + Δ M) g - (m + M + Δ M) a}{m g}$

Actividades

El programa interactivo genera aleatoriamente un valor del coeficiente cinético de rozamiento μ_k. El coeficiente estático se ha tomado arbitrariamente como μ_s= μ_k+0.2.

Se introduce

La masa del bloque en kg, actuando sobre la barra de desplazamiento titulada Masa

Se pulsa el botón titulado Nuevo

Se pulsa el botón izquierdo del ratón cuando el puntero está sobre una determinada pesa, se mantiene pulsado el botón izquierdo del ratón, se arrastra la pesa hasta que enganche debajo del extremo del hilo que cuelga de la polea, se deja de entonces, pulsar el botón izquierdo del ratón.

A continuación, se agrega otra pesa debajo de la anterior, y así sucesivamente, hasta que el bloque empiece a deslizar.

En la parte izquierda del applet, se guardan los pares de datos de la fuerza aplicada F y de la fuerza de rozamiento F_r.

Medida del coeficiente estático

Para medir el coeficiente tenemos que acercarnos lo máximo posible al valor de la fuerza μ_sN que hace que el bloque comience a deslizar con el juego de pesas disponible. En este caso, se dispone de un total de 12 pesas, cuatro de cada tipo:

25 g
100 g
500 g

Ponemos un ejemplo, que nos indica la forma de acercarnos al valor máximo de la fuerza de rozamiento.

Se pulsa el botón titulado Nuevo. Se empieza colocando una pesa de 500 g, el bloque no desliza. Se pone una segunda pesa de 500g, el bloque no desliza. Se añade la tercera pesa de 500 g, el bloque desliza
Se pulsa el botón titulado Nuevo. Se pone dos pesas de 500 g. Se añade una pesa de 100 g, el bloque no desliza. Se añade la segunda pesa de 100 g, el bloque desliza.
Se pulsa el botón titulado Nuevo. Se pone dos pesas de 500 g, y una pesa de 100 g. Se añade una pesa de 25 g, el bloque no desliza. Se añade la segunda pesa de 25 g, el bloque no desliza, se añade la tercera pesa de 25 g, el bloque desliza.

El valor de la fuerza F más cercana al valor máximo μ_sN (por defecto) es

F=(2·500+100+2·25)·10.0/1000 =11.5 N

La aceleración de la gravedad se ha tomado como g=10.0 m/s²

Si la masa del bloque es m=2 kg, N=mg=20 N. El coeficiente estático μ_s valdrá

μ_s=11.5/20=0.575

Medida del coeficiente cinético

Cuando añadimos la tercera pesa de ΔM=25 g, el bloque empieza a deslizar

La masa de las pesas que cuelgan es M+ΔM=1.15+0.025=1.175 kg

El bloque se desplaza x=1 m en t=1.22 s.

$\begin{array}{l} 1.0 = \frac{1}{2} a \cdot {1.22}^{2} a = 1.34 {m/s}^{2} \\ μ_{k} = \frac{(1.15 + 0.025) \cdot 10 - (2 + 1.15 + 0.025) 1.34}{2 \cdot 10} = 0.37 \end{array}$

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Se pulsa el botón titulado Nuevo, se arrastra con el puntero del ratón las pesas