• Inicio
• Dinámica
• Trabajo y energía

Movimiento de la partícula en contacto con el muelle

1. Comprimimos el muelle hasta una posición x₀ y luego se suelta. La partícula desliza bajo la acción de dos fuerzas:

• la fuerza que ejerce el muelle kx

• la fuerza de rozamiento que se opone al movimiento μmg

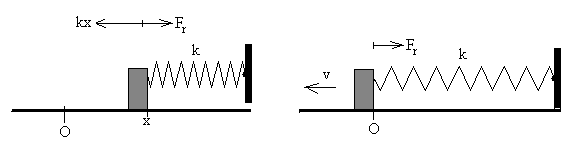
Si la máxima compresión del muelle es x₀, la partícula se moverá si kx₀> μmg, en caso contrario, permanecerá en equilibrio en dicha posición.

La ecuación del movimiento es

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-kx+\mu mg\frac{d^{2}x}{d{t}^2}+{\omega }^{2}x=\mu g}$

La solución de esta ecuación diferencial es

${\displaystyle x=A\sin (\omega t)+B\cos (\omega t)+\frac{\mu g}{{\omega }^2}}$

Las constantes A y B se determinan a partir de las condiciones iniciales: en el instante t=0, x=x₀ y dx/dt=0

${\displaystyle \begin{array}{l}x=\left(x_0-\frac{\mu g}{{\omega }^2}\right)\cos (\omega t)+\frac{\mu g}{{\omega }^2}\\ v=\frac{dx}{dt}=-\omega \left(x_0-\frac{\mu g}{{\omega }^2}\right)\sin (\omega t)\end{array}}$

Pueden ocurrir dos casos:

1.-Que la partícula se detenga antes de alcanzar el origen

2.-Que la partícula alcance el origen x=0, con velocidad final v

La partícula se detiene en el instante t=π/ω, su posición es

${\displaystyle x=2\frac{\mu g}{{\omega }^2}-x_0}$

Para que sobrepase el origen se tiene que cumplir que x₀>2μg/ω²

Llegamos a la misma conclusión desde el punto de vista energético. Solamente si la energía almacenada en el muelle es superior al trabajo de la fuerza de rozamiento, la partícula sobrepasa el origen

${\displaystyle \frac{1}{2}k{x}_0^2>\mu mg{x}_0{x}_0>\frac{2\mu g}{{\omega }^2}}$

La velocidad con la que llega al origen x=0 es

${\displaystyle \begin{array}{l}os(\omega t)=\frac{-\mu g/{\omega }^2}{x_0-\mu g/{\omega }^2}\\ v=-\omega \sqrt{x_0^2-2x_0\frac{\mu g}{{\omega }^2}}=-\sqrt{\frac{k}{m}{x}_0^2-2\mu g{x}_0}\end{array}}$

El mismo resultado que se obtiene aplicando el balance energético: El trabajo de la fuerza de rozamiento es igual a diferencia entre la energía final y la energía inicial

${\displaystyle -\mu mg{x}_0=\frac{1}{2}m{v}^2-\frac{1}{2}k{x}_0^2}$

2. Examinamos ahora la segunda situación: La partícula regresa al origen con velocidad v₀ y comprime el muelle

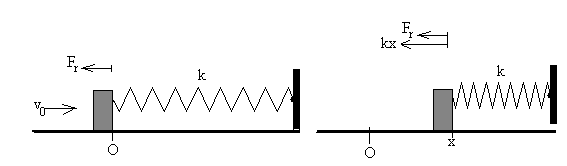
La ecuación del movimiento es

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-kx-\mu mg\frac{d^{2}x}{d{t}^2}+{\omega }^{2}x=-\mu g}$

La solución de esta ecuación diferencial es

${\displaystyle x=A\sin (\omega t)+B\cos (\omega t)-\frac{\mu g}{{\omega }^2}}$

Las constantes A y B se determinan a partir de las condiciones iniciales: en el instante t=0, x=0 y dx/dt=v₀

${\displaystyle \begin{array}{l}x=\frac{v_0}{\omega }\sin (\omega t)+\frac{\mu g}{{\omega }^2}\cos (\omega t)-\frac{\mu g}{{\omega }^2}\\ v=\frac{dx}{dt}=v_0\text{cos}(\omega t)-\frac{\mu g}{\omega }\sin (\omega t)\end{array}}$

La partícula se detiene v=0 en el instante t

${\displaystyle \tan (\omega t)=\frac{v_0\omega }{\mu g}}$

Teniendo en cuenta las relaciones trigonométricas

${\displaystyle \sin \alpha =\frac{\tan \alpha }{\sqrt{1+{\tan }^2\alpha }}\cos \alpha =\frac{1}{\sqrt{1+{\tan }^2\alpha }}}$

Llegamos a la siguiente expresión para la posición final de la partícula

${\displaystyle x=\frac{-\mu g+\sqrt{{\mu }^2{g}^2+{\omega }^2{v}_0^2}}{{\omega }^2}}$

El mismo resultado que se obtiene aplicando el balance energético: El trabajo de la fuerza de rozamiento es igual a diferencia entre la energía final y la energía inicial

${\displaystyle -\mu mgx=\frac{1}{2}k{x}^2-\frac{1}{2}m{v}_0^2}$

Trayectoria circular y parabólica

1. La partícula describe una trayectoria circular si la velocidad en la parte más baja del bucle es

${\displaystyle v_0\ge \sqrt{5Rg}}$

2. La partícula desliza hacia atrás cuando

${\displaystyle v_0\le \sqrt{2Rg}}$

3. Cuando la velocidad v₀ está comprendida entre estos dos valores, la partícula desliza por el bucle, describe un movimiento parabólico, choca con el bucle y vuelva a deslizar por el bucle tal como se muestra en la figura.

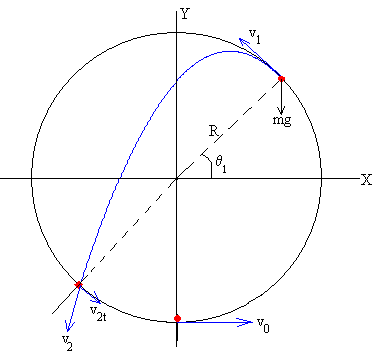
Para analizar este movimiento complejo, situamos el origen en el centro del bucle y medimos los ángulos desde el eje X. El nivel cero de energía potencial lo situamos en el eje X.

En la posición angular θ₁ la partícula deja de tener contacto con el bucle, la reacción N es nula

La ecuación de la dinámica del movimiento circular y el principio de conservación de la energía se escriben

${\displaystyle \begin{array}{l}mg\sin {\theta }_1=m\frac{v_1^2}{R}\\ \frac{1}{2}m{v}_0^2-mgR=\frac{1}{2}m{v}_1^2+mgR\sin {\theta }_1\end{array}}$

Combinando ambas ecuaciones determinamos el valor del ángulo θ₁

${\displaystyle v_0^2=2gR+3gR\sin {\theta }_1}$

Una vez que llega P₁ describe un movimiento parabólico, la velocidad y la posición de la partícula es

${\displaystyle \{\begin{array}{l}{v}_x=-v_1\sin {\theta }_1\\ v_y=v_1\cos {\theta }_1-gt\end{array}\{\begin{array}{l}x=R\cos {\theta }_1-v_1\sin {\theta }_{1}t\\ y=R\sin {\theta }_1+v_1\cos {\theta }_{1}t-\frac{1}{2}g{t}^2\end{array}}$

Choca con el bucle en el punto P₂ que es el punto de intersección entre la parábola y la circunferencia de radio R. Recordando que la ecuación de una circunferencia, cuando su centro está en el origen de coordenadas es

${\displaystyle \begin{array}{l}{x}^2+y^2=R^2\\ {\left(R\cos {\theta }_1-v_1\sin {\theta }_{1}t\right)}^2+{\left(R\sin {\theta }_1+v_1\cos {\theta }_{1}t-\frac{1}{2}g{t}^2\right)}^2=R^2\end{array}}$

Teniendo en cuenta que de la dinámica del movimiento circular

${\displaystyle v_1^2=Rg\sin {\theta }_1}$

Llegamos a la siguiente expresión simplificada

${\displaystyle t^{3}g\left(\frac{1}{4}gt-v_1\cos {\theta }_1\right)=0}$

El tiempo de vuelo de la partícula hasta que choca con el bucle es

${\displaystyle t=\frac{4v_1\cos {\theta }_1}{g}}$

La posición del punto de impacto P₂ y la velocidad de la partícula son, respectivamente

${\displaystyle \{\begin{array}{l}{v}_{2x}=-v_1\sin {\theta }_1\\ v_{2y}=-3v_1\cos {\theta }_1\end{array}\{\begin{array}{l}{x}_2=R\cos {\theta }_1-\frac{4v_1^2\sin {\theta }_1\cos {\theta }_1}{g}=-3R\cos {\theta }_1+4R{\cos }^3{\theta }_1\\ y_2=R\sin {\theta }_1-\frac{4v_1^2{\cos }^2{\theta }_1}{g}=R\sin {\theta }_1-4R\sin {\theta }_1{\cos }^2{\theta }_1\end{array}}$

Después del choque, supondremos que se anula la componente normal de la velocidad, y la partícula desliza sobre el bucle con la componente tangencial de la velocidad.

La componente normal de la velocidad se calcula mediante el producto escalar r₂·v₂

${\displaystyle v_{2r}=\frac{r_2·v_2}{R}{v}_{2t}^2=v_2^2-v_{2r}^2}$

El módulo del vector posición r₂ del punto P₂ es el radio R de la circunferencia

${\displaystyle \begin{array}{l}{v}_{2r}=8v_1\sin {\theta }_1{\cos }^3{\theta }_1\\ v_{2t}^2=v_1^2(1+8{\cos }^2{\theta }_1-64{\cos }^6{\theta }_1+64{\cos }^8{\theta }_1)\\ v_{2t}=v_1(1+4{\cos }^2{\theta }_1-8{\cos }^4{\theta }_1)\end{array}}$

La energía final de la partícula en el punto de impacto P₂ es

${\displaystyle E_2=\frac{1}{2}m{v}_{2t}^2+mg{y}_2=mgR\sin {\theta }_1(\frac{1}{2}-32{\cos }^6{\theta }_1+32{\cos }^8{\theta }_1)}$

La energía en el punto de impacto es menor que la energía de la partícula en el punto de lanzamiento

${\displaystyle E=\frac{1}{2}m{v}_0^2-mgR=\frac{1}{2}m{v}_1^2+mgR\sin {\theta }_1=\frac{3}{2}mgR\sin {\theta }_1}$

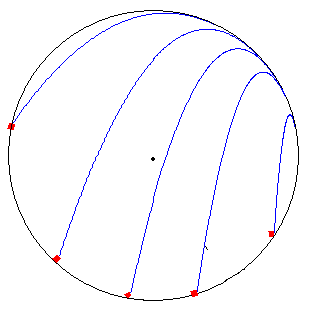
En la figura se muestran, las trayectorias parabólicas seguidas por la partícula, para distintos valores de la velocidad inicial v₀ en la parte inferior del bucle.

Referencias

De la sección Trayectoria circular y parabólica

Gorielay A., Boulanger P, Leroy J., Toy models: The jumping pendulum. Am. J. Phys. 74 (9) September 2006, pp. 784-78

Curso Interactivo de Física en Internet © Ángel Franco García