El bucle

Escultura "el bucle". Juanjo Novella. Plaza de Cruces. Baracaldo (Vizcaya)

Se propone un problema que permite al lector practicar con todos los aspectos relacionados con la dinámica de una partícula.

Se lanza una partícula mediante un dispositivo que consiste esencialmente en un muelle comprimido. Primero, la partícula desliza a lo largo de un plano horizontal. Luego, entra en un bucle y a continuación, si consigue describir el rizo, pasa a un plano inclinado.

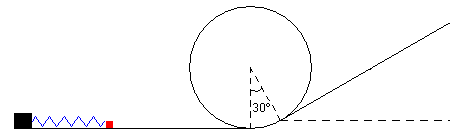
Se supone que existe rozamiento entre la partícula y los planos horizontal e inclinado, pero no existe rozamiento en el bucle, por razón de simplicidad de cálculo.

Descripción

En esta sección analizaremos cada una de las etapas en las que se puede dividir el bucle

Plano horizontal A-B

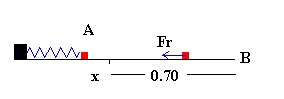
bucle6.gif (680 bytes)

Si comprimimos el muelle una distancia x y luego, lo soltamos en la posición A, podemos calcular la velocidad de la partícula en la entrada B del bucle, aplicando las ecuaciones del balance de energía.

En la posición A, la partícula solamente tiene energía potencial elástica

$E_{A} = \frac{1}{2} k x^{2}$

Siendo k la constante elástica del muelle, que se transforma en energía cinética en la posición B

$E_{B} = \frac{1}{2} m v_{B}^{2}$

En el trayecto AB se pierde energía debido al rozamiento

W_AB=-F_r(x+0.7)=-μ_kmg(x+0.7)

Donde x+0.7 es la distancia entre los puntos A y B.

De la ecuación del balance energético W_AB=E_B-E_Aobtenemos v_B

$\frac{1}{2} k x^{2} = \frac{1}{2} m v_{B}^{2} + μ_{k} m g (x + 0.7)$

En la sección "Movimiento de la partícula en contacto con el muelle" se proporciona un análisis más detallado del movimiento de la partícula.

Bucle

El análisis del comportamiento de la partícula en el bucle es algo más complejo y pueden ocurrir alguna de las siguientes situaciones:

Describe el bucle

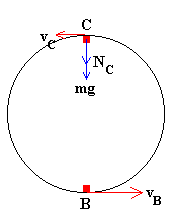bucle7.gif (1127 bytes) De la conservación de la energía (en el bucle no hay rozamiento) calculamos la velocidad de la partícula en la parte superior del bucle C, conocida la velocidad en la parte inferior B.

$\frac{1}{2} m v_{B}^{2} = \frac{1}{2} m v_{C}^{2} + 2 m g R$

Siendo R el radio del bucle

Ahora bien, si la velocidad de la partícula en la posición C es inferior a un valor mínimo, no describirá el bucle.

De las ecuaciones de la dinámica del movimiento circular tenemos que

$m g + N_{C} = m \frac{v_{C}^{2}}{R}$

Siendo N_C la fuerza normal en C, o fuerza que ejerce el raíl sobre la partícula en dicha posición. La velocidad mínima se obtiene cuando N_C=0.

$v_{C m í n} = \sqrt{R g} v_{B}^{2} = 5 R g$

Podemos ahora pensar qué ocurre si no se alcanza la velocidad mínima v_Cmín

Asciende a lo largo del bucle hasta que su velocidad es cero

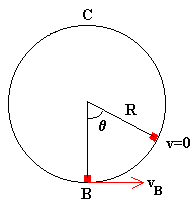Aplicando el principio de conservación de la energía calculamos el ángulo θ

$\frac{1}{2} m v_{B}^{2} = m g R (1 - \cos θ)$

Si el ángulo es mayor que 90º o π /2.
El ángulo θ se calcula mediante la dinámica del movimiento circular y el principio de conservación de la energía.

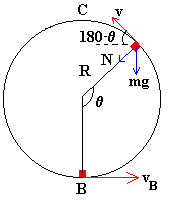
$\begin{array}{l} N + m g \cos (180 - θ) = m \frac{v^{2}}{R} \\ \frac{1}{2} m v_{B}^{2} = \frac{1}{2} m v^{2} + m g R (1 + \cos (180 - θ)) \end{array}$

La partícula deja de tener contacto con el bucle en el instante en el que la fuerza normal es cero, N=0. Por lo que

$v_{B}^{2} = g R (2 + 3 \cos (180 - θ))$

En dicho instante, la partícula se mueve bajo la única fuerza de su propio peso describiendo un movimiento curvilíneo bajo la aceleración constante de la gravedad o un tiro parabólico.

Situamos los ejes en el centro del bucle. La posición de lanzamiento, tal como se ve en la figura anterior, es

x₀=R·sin(180-θ )
y₀=R·cos(180-θ )

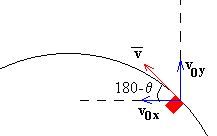Las velocidades iniciales, en el momento del lanzamiento, son

v_0x=-v·cos(180-θ )
v_0y=v·sin(180-θ )

En la sección titulada "Trayectoria circular y parabólica" analizaremos con detalle esta interesante combinación de movimientos.

En las situaciones 1 y 2, la partícula regresa a la posición B con la misma velocidad con la que entró en el bucle, ya que como se ha mencionado el bucle no tiene rozamiento.

Plano inclinado

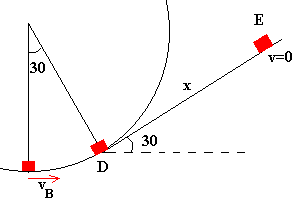
Si la partícula describe el bucle entra en el plano inclinado con una velocidad v_D que se calcula mediante el principio de conservación de la energía

$\frac{1}{2} m v_{B}^{2} = \frac{1}{2} m v_{D}^{2} + m g R (1 - \cos 30)$

Una vez en el plano, el móvil se frena debido a la componente del peso a lo largo del plano inclinado y a la fuerza de rozamiento. La partícula recorre una distancia x a lo largo del plano inclinado hasta que se para.

El balance energético o las ecuaciones de la dinámica del movimiento rectilíneo nos permiten calcular x.

$\begin{array}{l} E_{D} = \frac{1}{2} m v_{D}^{2} E_{E} = m g x \sin 30 º \\ W_{D E} = - F_{r} x = - μ m g \cos 30 x \end{array}$

Aplicando el balance energético W_DE=E_E-E_D despejamos x.

$- μ m g \cos 30 º \cdot x = m g x \sin 30 º - \frac{1}{2} m v_{D}^{2}$

Ejemplos

Constante del muelle k=500 N/m
Radio del bucle R=0.5 m
Coeficiente de rozamiento μ=0.2
La masa de la partícula se ha fijado en m=1 kg

Examinamos las distintas situaciones que se producen cuando se comprime el muelle x.

Ejemplo 1

Se comprime el muelle x=0.24 cuando se actúa con el puntero del ratón sobre el pequeño cuadrado de color rojo, que representa una partícula de masa m=1 kg.

La velocidad con la que llega al punto B, inicio de la pista circular es

$\frac{1}{2} 500 \cdot {0.24}^{2} = \frac{1}{2} 1 v_{B}^{2} + 0.2 \cdot 1 \cdot 9.8 \cdot (0.24 + 0.7) v_{B} = 5.01 m/s$

La partícula pasa por el punto mas alto C de la pista circular con una velocidad de

$\frac{1}{2} 1 \cdot {5.01}^{2} = \frac{1}{2} 1 v_{c}^{2} + 2 \cdot 1 \cdot 9.8 \cdot 0.5 v_{c} = 2.34 m/s, ω = \frac{v_{c}}{R} = 4.70 rad/s$

Regresa al punto B, parte inferior de la pista circular con la misma velocidad v_B=5.01 m/s o una velocidad angular de ω=10.02 rad/s.

Llega al punto D comienzo de la pista inclinada 30º con una velocidad

$\frac{1}{2} 1 \cdot {5.01}^{2} = \frac{1}{2} 1 v_{D}^{2} + 1 \cdot 9.8 \cdot 0.5 \cdot (1 - \cos 30 º) v_{D} = 4.87 m/s$

Calculamos el máximo desplazamiento D de la partícula a lo largo del plano inclinado

$- 0.2 \cdot 1 \cdot 9.8 \cdot \cos 30 º \cdot x = 1 \cdot 9.8 \cdot x \cdot \sin 30 º - \frac{1}{2} 1 \cdot {4.87}^{2} x = 1.80 m$

Ejemplo 2

Se comprime ahora el muelle x=0.2 m

La velocidad con la que llega al punto B, inicio de la pista circular es

$\frac{1}{2} 500 \cdot {0.20}^{2} = \frac{1}{2} 1 v_{B}^{2} + 0.2 \cdot 1 \cdot 9.8 \cdot (0.20 + 0.7) v_{B} = 4.05 m/s$

La partícula desliza por la pista circular hasta que la velocidad sea cero o la reacción N se hace cero. En este caso, se analiza la segunda situación

${4.05}^{2} = 9.8 \cdot 0.5 (2 + 3 \cos (180 - θ)) θ = 117 º$

Su velocidad v en esta posición es

$\frac{1}{2} 1 \cdot {4.05}^{2} = \frac{1}{2} 1 \cdot v^{2} + 1 \cdot 9.8 \cdot 0.5 (1 + \cos (180 - 117)) v = 1.49 m/s, ω = 2.98 rad/s$

La partícula describe una parábola hasta que choca con la parte inferior de la pista circular.

Ejemplo 3

Se comprime ahora el muelle x=0.1 m

La velocidad con la que llega al punto B, inicio de la pista circular es

$\frac{1}{2} 500 \cdot {0.1}^{2} = \frac{1}{2} 1 v_{B}^{2} + 0.2 \cdot 1 \cdot 9.8 \cdot (0.10 + 0.7) v_{B} = 1.36 m/s$

La partícula desliza por la pista circular hasta que la velocidad sea cero

$\frac{1}{2} 1 \cdot {1.36}^{2} = 1 \cdot 9.8 \cdot 0.5 \cdot (1 - \cos θ) θ = 35.9 º$

Retrocede pasando por B, parte inferior de la pista circular con la misma velocidad ya que no hay rozamiento, desliza por la pista horizontal, y puede llegar a A o puede pararse antes.

$- 0.2 \cdot 1 \cdot 9.8 \cdot 0.7 = \frac{1}{2} 1 \cdot v_{A}^{2} - \frac{1}{2} 1 \cdot {1.36}^{2} v_{A}^{2} = - 0.88$

La partícula no llega a la posición A, se para a la distancia

$- 0.2 \cdot 1 \cdot 9.8 \cdot x = 0 - \frac{1}{2} 1 \cdot {1.36}^{2} x = 0.47 m$

Se para a una distancia de 47 cm medido desde B o de 70-47=23 cm medido desde el origen A.

Actividades

Cuando la partícula está en el origen, situamos el puntero del ratón sobre la partícula de color rojo, con el botón izquierdo del ratón pulsado, se arrastra la partícula y se comprime el muelle la distancia x deseada. A continuación, se suelta el botón izquierdo del ratón. La partícula empieza a moverse hacia el bucle.

Para volver a repetir la experiencia, se sitúa la partícula en el origen pulsando el botón titulado Inicio.

El botón titulado Pausa sirve para parar momentáneamente el movimiento, que se reanuda cuando se vuelve a pulsar el mismo botón titulado ahora Continua. Pulsando en el botón titulado Paso se observa la posición de la partícula en cada intervalo de tiempo, paso a paso.

Se pueden cambiar los parámetros siguientes:

El valor de la constante elástica k del muelle, en el control de edición titulado Constante del muelle.
El coeficiente de rozamiento en el control de edición titulado Coeficiente de rozamiento, dentro de ciertos límites (0- 0.7). Introduciendo 0 suponemos que no hay rozamiento. Solamente hay rozamiento en la pistas horizontal e inclinada, pero no hay rozamiento en la circular.
El radio del bucle en el control de edición Radio del bucle, dentro del límite 0.2 a 0.5 m.
La masa de la partícula se ha fijado en 1 kg

El programa es flexible y nos permite practicar la mayor parte de las situaciones que se describen en la dinámica:

La dinámica del movimiento rectilíneo uniformemente acelerado (plano inclinado)
La dinámica del movimiento circular (bucle)
Conservación de la energía (bucle)
Balance energético cuando actúan fuerzas no conservativas, la fuerza de rozamiento (plano inclinado y plano horizontal)

A la izquierda del applet podemos observar de forma cualitativa el balance energético. El círculo mayor es la energía total, y los colores indican las proporciones de cada clase de energía.

En color rojo, se muestra la energía disipada debido al rozamiento en los planos horizontal e inclinado, o en el choque con el raíl cuando no consigue describir el rizo.
En color amarillo, se muestra la energía potencial (gravitatoria o elástica del muelle)
En color azul, la energía cinética

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Arrastre hacia la izquierda con el puntero del ratón, el pequeño cuadrado de color rojo