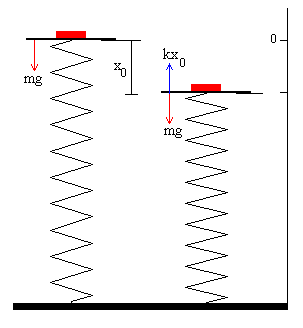
Se coloca un bloque sobre un muelle vertical sin deformar.
Consideremos un bloque de masa m que se coloca sobre un muelle vertical de constante k y de longitud L0 sin deformar. El conjunto formado por el muelle y el cuerpo empezará a oscilar alrededor de una altura de equilibrio, y con una amplitud que vamos a determinar.
Descripción
El bloque unido al muelle describirá un Movimiento Armónico Simple de frecuencia angular
La posición de equilibrio se determina a partir de la condición de que
la resultante de las fuerzas que actúan sobre el cuerpo sea nula.
La posición x0 será tal que mg=kx0
La ecuación del movimiento del sistema oscilante es
x=-x0+A·sin(ω t+φ )
Derivando con respecto del tiempo, obtenemos la expresión de la velocidad v.
v=dx/dt=Aω ·cos(ω t+φ )
En el instante t=0, el móvil se encuentra en la posición x=0 con velocidad nula v=0
Con estos datos determinamos la amplitud A y la fase inicial φ .
0=-x0+A·sinφ
0=Aω ·cosφ
la fase inicial es φ =π/2 y la amplitud A=x0
La ecuación del movimiento es
x=-x0+x0·sin(ω t+π/2) o bien,
x=x0·(-1+cos(ω t))
Balance energético
El cuerpo está sometido a la acción de dos fuerzas conservativas, el peso cuya energía potencial es mgh, y la fuerza que ejerce el muelle cuya energía potencial es kx2/2.
El nivel cero de energía potencial gravitatoria lo podemos poner donde queramos. El nivel cero de la energía potencial elástica es aquél en el que el muelle se encuentra sin deformar.
Ponemos el nivel cero de energía potencial gravitatoria en x=-x0, en la posición de equilibrio.
En la situación de partida
- Energía cinética Ek=0
- Energía potencial elástica Epe=0, el muelle se encuentra sin deformar
- Energía potencial gravitatoria Ep=mgx0.
La energía total E=mgx0, se va a distribuir entre las otras formas de energía sin que la suma total cambie.
Cuando el cuerpo pasa por la situación de equilibrio.
- Energía cinética Ek=mv2/2
- Energía potencial elástica Epe=kx02/2, el muelle se ha deformado x0
- Energía potencial gravitatoria Ep=0,
Cuando el cuerpo pasa por la posición más baja x= -2x0, la velocidad es cero, v=0
- Energía cinética Ek=0
- Energía potencial elástica Epe=2kx02, el muelle se ha deformado 2x0
- Energía potencial gravitatoria Ep= -mgx0, el cuerpo
se encuentra x0 por debajo del nivel cero de energía potencial
Ejemplo:
Sea m=10 kg
Sea k=1000 N/m
El periodo de las oscilaciones es
La posición de equilibrio es
1000·x0=10·9.8, por lo que x0=0.098 m=9.8 cm
La posición del cuerpo en función del tiempo es
x=9.8·(-1+cos(10t)) cm
| Tiempo t (s) | Posición x (cm) |
| 0 | 0 |
| P/4 | -9.8 |
| P/2 | -19.6 |
| 3P/2 | -9.8 |
| 2P | 0 |
A la derecha del applet, vemos la representación de la posición x del cuerpo en función del tiempo t.
La energía total del cuerpo es E=-10·9.8·0.098=9.6 J
Actividades
Se introduce
- La constante elástica del muelle (N/m), en el control de edición titulado Constante elástica
- La masa del cuerpo (kg), en el control de edición titulado Masa del bloque
Se pulsa el botón titulado Inicio para que el programa verifique los datos. Si estos son correctos, se pulsa a continuación el botón titulado Empieza. Observamos el movimiento del sistema oscilante
Cada vez que se realice un nueva "experiencia" se pulsa el botón titulado Inicio.
Las tras clases de energías (cinética, potencial, potencial elástica) se representan mediante barras de colores. Podemos observar que la energía cinética y la energía potencial elástica son ambas positivas. Pero la energía potencial gravitatoria puede se positiva o negativa, ya que hemos puesto el nivel cero de energía potencial en la posición de equilibrio x0. La suma de las tres clases de energías es constante.