• Inicio
• Dinámica
• Trabajo y energía

Fuerza conservativa. Energía potencial

Un fuerza es conservativa cuando el trabajo de dicha fuerza es igual a la diferencia entre los valores inicial y final de una función que solo depende de las coordenadas. A dicha función se le denomina energía potencial.

${\displaystyle {\displaystyle \underset{A}{\overset{B}{\int }}F·dr}=E_{pA}-E_{pB}{E}_p=E_p(x,y,z)}$

El trabajo de una fuerza conservativa no depende del camino seguido para ir del punto A al punto B.

El trabajo de una fuerza conservativa a lo largo de un camino cerrado es cero.

${\displaystyle {\displaystyle \oint F·dr=0}}$

Ejemplo

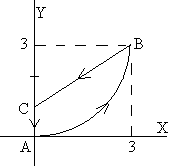Sobre una partícula actúa la fuerza F=2xyi+x²j N

Calcular el trabajo efectuado por la fuerza a lo largo del camino cerrado ABCA.

• La curva AB es el tramo de parábola y=x²/3.
• BC es el segmento de la recta que pasa por los puntos (0,1) y (3,3) y
• CA es la porción del eje Y que va desde el origen al punto (0,1)

 

El trabajo infinitesimal dW es el producto escalar del vector fuerza por el vector desplazamiento

dW=F·dr=(F_xi+F_yj)·(dxi+dyj)=F_xdx+F_ydy

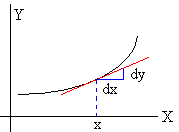Las variables x e y se relacionan a través de la ecuación de la trayectoria y=f(x), y los desplazamientos infinitesimales dx y dy se relacionan a través de la interpretación geométrica de la derivada dy=f’(x)·dx. Donde f’(x) quiere decir, derivada de la función f(x) con respecto a x.

Vamos a calcular el trabajo en cada unos de los tramos y el trabajo total en el camino cerrado.

 

• Tramo AB

Trayectoria y=x²/3, dy=(2/3)x·dx.

${\displaystyle \begin{array}{l}dW=F_{x}dx+F_{y}dy=2x\frac{x^2}{3}dx+x^2\frac{2}{3}xdx=\frac{4}{3}{x}^{3}dx\\ W_{AB}={\displaystyle \underset{0}{\overset{3}{\int }}\frac{4}{3}{x}^{3}dx}=27\text{J}\end{array}}$

• Tramo BC

La trayectoria es la recta que pasa por los puntos (0,1) y (3,3). Se trata de una recta de pendiente 2/3 y cuya ordenada en el origen es 1.

y=(2/3)x+1, dy=(2/3)·dx

${\displaystyle \begin{array}{l}dW=F_{x}dx+F_{y}dy=2x\left(\frac{2}{3}x+1\right)dx+x^2\frac{2}{3}dx=(2x^2+2x)dx\\ W_{BC}={\displaystyle \underset{3}{\overset{0}{\int }}(2x^2+2x)dx}=-27\text{J}\end{array}}$

• Tramo CD

La trayectoria es la recta x=0, dx=0, La fuerza F=0 y por tanto, el trabajo W_CA=0

• El trabajo total

W_ABCA=W_AB+W_BC+W_CA=27+(-27)+0=0

El peso es una fuerza conservativa

Calculemos el trabajo de la fuerza peso F=-mg j cuando el cuerpo se desplaza desde la posición A cuya ordenada es y_A hasta la posición B cuya ordenada es y_B.

${\displaystyle {\displaystyle \underset{A}{\overset{B}{\int }}F·dr}={\displaystyle \underset{A}{\overset{B}{\int }}(-mg\widehat{j})\cdot (dx\widehat{i}+dy\widehat{j})}={\displaystyle \underset{A}{\overset{B}{\int }}-mgdy}=mg{y}_A-mg{y}_B}$

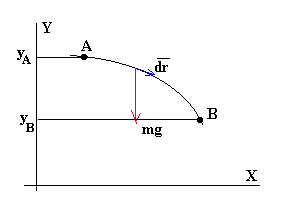
La energía potencial E_p correspondiente a la fuerza conservativa peso tiene la forma funcional

${\displaystyle E_p=mgy+c}$

Donde c es una constante aditiva que nos permite establecer el nivel cero de la energía potencial.

La fuerza que ejerce un muelle es conservativa

Como vemos en la figura cuando un muelle se deforma x, ejerce una fuerza sobre la partícula proporcional a la deformación x y de signo contraria a ésta.

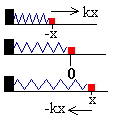Para x>0, F=-kx

Para x<0, F=kx

El trabajo de esta fuerza es, cuando la partícula se desplaza desde la posición x_A a la posición x_B es

${\displaystyle {\displaystyle \underset{A}{\overset{B}{\int }}F·dx}={\displaystyle \underset{A}{\overset{B}{\int }}-kxdx}=\frac{1}{2}k{x}_A^2-\frac{1}{2}k{x}_B^2}$

La función energía potencial E_p correspondiente a la fuerza conservativa F vale

${\displaystyle E_p(x)=\frac{1}{2}k{x}^2+c}$

El nivel cero de energía potencial se establece del siguiente modo: cuando la deformación es cero x=0, el valor de la energía potencial se toma cero, E_p=0, de modo que la constante aditiva vale c=0.

${\displaystyle F=-kx{E}_p=\frac{1}{2}k{x}^2}$

Principio de conservación de la energía

Si solamente una fuerza conservativa F actúa sobre una partícula, el trabajo de dicha fuerza es igual a la diferencia entre el valor inicial y final de la energía potencial

${\displaystyle {\displaystyle \underset{A}{\overset{B}{\int }}F·dr}=E_{pA}-E_{pB}}$

Como hemos visto en el apartado anterior, el trabajo de la resultante de las fuerzas que actúa sobre la partícula es igual a la diferencia entre el valor final e inicial de la energía cinética.

${\displaystyle {\displaystyle \underset{A}{\overset{B}{\int }}F·dr}=E_{kB}-E_{kA}}$

Igualando ambos trabajos, obtenemos la expresión del principio de conservación de la energía

E_kA+E_pA=E_kB+E_pB

La energía mecánica de la partícula (suma de la energía potencial más cinética) es constante en todos los puntos de su trayectoria.

Comprobación del principio de conservación de la energía

Un cuerpo de 2 kg se deja caer desde una altura de 3 m. Calcular

1. La velocidad del cuerpo cuando está a 1 m de altura y cuando llega al suelo, aplicando las fórmulas del movimiento rectilíneo uniformemente acelerado

2. La energía cinética potencial y total en dichas posiciones

Tomar g=10 m/s²

• Posición inicial x=3 m, v=0.

E_p=2·10·3=60 J, E_k=0, E_A=E_k+E_p=60 J

• Cuando x=1 m

${\displaystyle \begin{array}{l}1=3+\frac{1}{2}(-10)t^{2}t=\sqrt{2/5}\text{s}\\ v=-10·tv=\sqrt{40}\text{m/s}\end{array}}$

E_p=2·10·1=20 J, E_k=40, E_B=E_k+E_p=60 J

• Cuando x=0 m

${\displaystyle \begin{array}{l}0=3+\frac{1}{2}(-10)t^{2}t=\sqrt{3/5}\text{s}\\ v=-10·tv=\sqrt{60}\text{m/s}\end{array}}$

E_p=2·10·0=0 J, E_k=60, E_C=E_k+E_p=60 J

La energía total del cuerpo es constante. La energía potencial disminuye y la energía cinética aumenta.

Curso Interactivo de Física en Internet © Ángel Franco García