La fuerza que ejerce la presión atmosférica

En esta página, se estudia un sistema de masa variable, y se comprueba los efectos de la fuerza que ejerce la presión atmosférica.

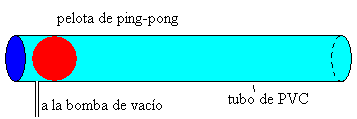
Disponemos de un tubo de PVC de longitud L y sección A, sellado por ambos extremos, que tiene en su interior una pelota de ping-pong. El diámetro del tubo es un poco mayor que el diámetro de la pelota, de modo que ésta pueda moverse a lo largo del tubo.

Se retira el aire en el interior del tubo, conectándolo a una bomba de vacío. Se rompe con un objeto punzante la lámina que sella el extremo izquierdo, el aire penetra en el interior del tubo y empuja a la pelota, que se mueve a lo largo del tubo, hasta que llega al otro extremo, rompe la tapa derecha y sale a gran velocidad.

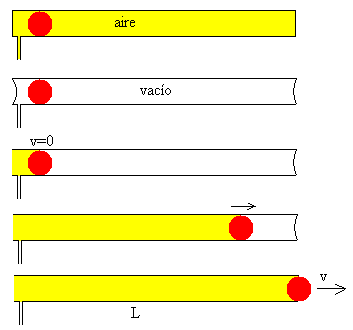
Tenemos de este modo, un cañón cuyo proyectil es impulsado por la fuerza que ejerce la presión atmosférica. La sucesión de imágenes de la figura nos permite entender como opera este dispositivo.

Movimiento del proyectil en el tubo de lanzamiento

Supongamos que el proyectil tiene sección A y masa m. La fuerza que ejerce la presión atmosférica p₀ sobre el proyectil es p₀·A. Pero esta fuerza ha de acelerar el proyectil de masa m y la columna de aire de masa ρAx por detrás del proyectil (en color amarillo en la figura).

La ecuación del movimiento es

$p_{0} A = \frac{d}{d t} ((m + ρ A x) v)$

Si el proyectil parte del reposo v=0 en el instante t=0, la expresión de la velocidad v en función del tiempo t es

$p_{0} A t = (m + ρ A x) v$

Para obtener la posición x del proyectil en función del tiempo t tenemos que integrar

$p_{0} A t = (m + ρ A x) \frac{d x}{d t}$

con la condición inicial de que en el instante t=0, el proyectil parte del origen x=0.

$m x + \frac{1}{2} ρ A x^{2} = \frac{1}{2} p_{0} A t^{2} x = \frac{\sqrt{m^{2} + ρ A^{2} p_{0} t^{2}} - m}{ρ A}$

La velocidad v del proyectil en función del tiempo es

$v = \frac{d x}{d t} = \frac{A p_{0} t}{\sqrt{m^{2} + ρ A^{2} p_{0} t^{2}}} = {(\frac{m^{2}}{p_{0}^{2} A^{2} t^{2}} + \frac{ρ}{p_{0}})}^{- 1 / 2}$

Para un cañón infinitamente largo, cuando t→∞, la velocidad final tiende hacia

$v_{\infty} = \sqrt{\frac{p_{0}}{ρ}}$

Esta velocidad puede comparase con la velocidad del sonido en el aire

$v_{s} = \sqrt{\frac{γ p_{0}}{ρ}}$

Donde γ=1.4 es el índice adiabático del aire

Ejemplo:

Una pelota de ping-pong tiene una masa m=2.5 g y un diámetro de 3.8 cm, o una sección trasversal de A=1.13·10^-3 m², la densidad del aire es ρ=1.29 kg/m³ y la presión atmosférica es de p₀=1.013·10⁵ Pa

Calculamos la velocidad final del proyectil en un tubo de longitud L=1.5 m

$\begin{array}{l} m L + \frac{1}{2} ρ A L^{2} = \frac{1}{2} p_{0} A t^{2} \\ 0.0025 \cdot 1.5 + \frac{1}{2} 1.29 \cdot 1.13 \cdot 10^{- 3} \cdot {1.5}^{2} = \frac{1}{2} 1.013 \cdot 10^{5} \cdot 1.13 \cdot 10^{- 3} t^{2} t = 0.0097 s \\ v = \frac{A p_{0} t}{\sqrt{m^{2} + ρ A^{2} p_{0} t^{2}}} = \frac{1.13 \cdot 10^{- 3} \cdot 1.013 \cdot 10^{5} \cdot 0.0097}{\sqrt{{0.0025}^{2} + 1.29 \cdot {(1.13 \cdot 10^{- 3})}^{2} \cdot 1.013 \cdot 10^{5} \cdot {0.0097}^{2}}} = 237.0 m/s \end{array}$

Movimiento del proyectil fuera del tubo.

Para simular el movimiento de la pelota de ping-pong fuera del tubo de lanzamiento, suponemos que sobre el proyectil actúa una fuerza de rozamiento proporcional al cuadrado de la velocidad.

$m \frac{d v}{d t} = - k v^{2}$

Integramos esta ecuación sabiendo que en el instante t=t₀, el móvil lleva una velocidad v₀, es decir, la velocidad final al salir del tubo de lanzamiento.

$\int_{v_{0}}^{v} \frac{d v}{v^{2}} = - \frac{k}{m} \int_{t_{0}}^{t} d t \frac{1}{v} = \frac{1}{v_{0}} + \frac{k}{m} (t - t_{0})$

Integramos de nuevo, para obtener la posición x en función del tiempo, sabiendo que en el instante t₀ parte de la posición x₀=L.

$\int_{L}^{x} d x = \int_{t_{0}}^{t} \frac{d t}{\frac{1}{v_{0}} + \frac{k}{m} (t - t_{0})} x = L + \frac{m}{k} \ln (1 + \frac{k}{m} v_{0} (t - t_{0}))$

Actividades

Se introduce

La masa en gramos de la pelota de ping-pong, actuando en la barra de desplazamiento titulada Masa pelota
La longitud del tubo, en metros, actuando en la barra de desplazamiento titulada Longitud tubo
La densidad del aire vale ρ=1.29 kg/m³
La el área de la sección trasversal de la pelota de ping-pong se ha fijado en A=1.13·10^-3 m²
La presión atmosférica vale p₀=1.013·105 Pa

Se pulsa el botón titulado Empieza

Primero, se conecta el tubo a una bomba de vacío, y un manómetro nos señala la disminución de la presión en el tubo sellado por ambos extremos.

A continuación, se observa el movimiento del proyectil (en color rojo) a lo largo del tubo, y la columna de aire (en color amarillo) detrás.

En la parte superior del applet, se representa, la velocidad v del proyectil en función de la posición x, medida desde la parte izquierda del tubo que se toma como origen.

El proyectil alcanza una velocidad máxima al final del tubo y luego, disminuye debido al rozamiento con el aire. En esta “experiencia” anotaremos la velocidad final v₀ y la relacionaremos con la masa m del proyectil y con la longitud L del tubo.

Referencias

Ayars E., Buchholtz L. Analysis of the vacuum cannon. Am. J. Phys. 72 (7) July 2004, pp. 961-963.