Una cuerda que desliza sobre una mesa

El movimiento de una cuerda que desliza sin rozamiento sobre una mesa y cae por el borde de la misma, es un ejemplo típico de movimiento de un sistema de masa variable.

Ecuación del movimiento

Sea una cuerda uniforme de longitud l, de densidad lineal ρ, que desliza sin rozamiento sobre una mesa horizontal y que cae por uno de sus bordes, tal como se muestra en la figura.

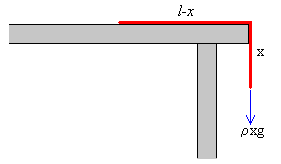
En un determinado instante t, la longitud del segmento vertical de la cuerda que cuelga del borde de la mesa es x. La fuerza que actúa sobre toda la cuerda es el peso de la parte vertical. El peso de la parte horizontal l-x se equilibra con la reacción de la mesa. La segunda ley de Newton se escribe

$ρ l \frac{d^{2} x}{d t^{2}} = ρ g x$

La ecuación del movimiento de la cuerda homogénea es independiente del valor de su densidad ρ.

La solución de esta ecuación diferencial es

$\begin{array}{l} x = A \cosh (\sqrt{\frac{g}{l}} t) + B \sinh (\sqrt{\frac{g}{l}} t) \\ v = \frac{d x}{d t} = \sqrt{\frac{g}{l}} (A \sinh (\sqrt{\frac{g}{l}} t) + B \cosh (\sqrt{\frac{g}{l}} t)) \end{array}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales. Supongamos que en el instante inicial t=0, x=x₀, v=0, cuelga del borde de la mesa una porción x₀ de la cuerda, y se suelta.

$\begin{array}{l} x = x_{0} \cosh (\sqrt{\frac{g}{l}} t) \\ v = \sqrt{\frac{g}{l}} x_{0} sinh (\sqrt{\frac{g}{l}} t) \end{array}$

Balance energético

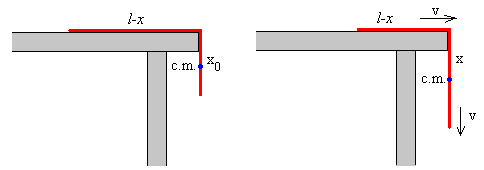
Situamos el nivel cero de energía potencial en el borde de la mesa.

La energía inicial es la energía potencial del centro de masas (c.m.) de la parte de la cuerda que cuelga del borde de la mesa, cuya masa es ρx₀.

$E = - ρ x_{0} g \frac{x_{0}}{2} = - ρ g \frac{x_{0}^{2}}{2}$

La energía de la cuerda en el instante t es la suma de:

La energía cinética E_k de toda la cuerda, cuya masa es ρl, que se mueve con velocidad v

$E_{k} = \frac{1}{2} ρ L v^{2}$

La energía potencial del c.m. de la parte de la cuerda que cuelga del borde de la mesa, cuya masa es ρx.

$E_{p} = - ρ x g \frac{x}{2} = - ρ g \frac{x^{2}}{2}$

Aplicamos el principio de conservación de la energía

$- ρ g \frac{x_{0}^{2}}{2} = - ρ g \frac{x^{2}}{2} + \frac{1}{2} ρ l v^{2}$

Introduciendo las expresiones de x y de v en función del tiempo y teniendo en cuenta que senh²z-cosh²z=-1, comprobamos que se cumple el principio de conservación de la energía.

Si derivamos la ecuación de la energía respecto del tiempo

$- ρ g x \frac{d x}{d t} + ρ l v \frac{d v}{d t} = 0$

Volvemos a obtener la ecuación del movimiento

Ejemplo

Sea x₀=0.1 y l=1.0

El tiempo que tarda el extremo de la cuerda en llegar al borde de la tabla x=1.0, es

$1.0 = 0.1 \cosh (\sqrt{9.8} t) t = 0.956 s$

La velocidad de la cuerda en este instante es

v=3.11 m/s

En el instante t=0.5 s

La parte de la cuerda que cuelga del borde de la mesa y su velocidad son, respectivamente

$\begin{array}{l} x = 0.1 \cosh (\sqrt{9.8} \cdot 0.5) = 0 .25 m \\ v = \sqrt{9.8} \cdot 0.1 \cdot \sinh (\sqrt{9.8} \cdot 0.5) = 0.72 m/s \end{array}$

La energía potencial es

E_p=-0.25²·9.8/2=-0.305 J

La energía cinética

E_k=1.0·0.72²/2=0.256 J

La energía total es

E=E_p+E_k=-0.049 J

Que es igual a la energía potencial inicial

E_p=-0.1²·9.8/2=-0.049 J

Fuerzas sobre la cuerda en el borde de la mesa

La ecuación del movimiento se ha deducido suponiendo que la cuerda mantiene en todo momento la forma de "L invertida”. Pero cómo es posible mantener un ángulo de 90º entre las dos partes de la cuerda desde el mismo momento en el que ésta se pone en movimiento. La suposición de que la cuerda se dobla bruscamente 90º en el borde de mesa, anulándose instantáneamente el momento lineal horizontal y continuando su movimiento hacia abajo, no es realista. El problema es por tanto, mucho más complejo tal como se describe en el segundo artículo citado en las referencias.

La segunda ley de Newton para este sistema bidimensional

$F = \frac{d p}{d t}$

F es la suma de todas las fuerzas exteriores
p es la suma de los momentos lineales de las partículas que forman el sistema

Momento lineal p

a lo largo del eje X, p_x=-ρ(l-x)·v
a lo largo del eje Y, p_y= ρx·v

Fuerzas exteriores F

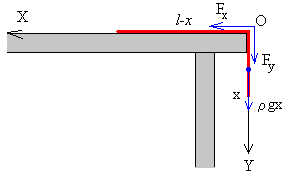
El peso de la porción vertical x de la cuerda ρgx. El peso de la parte de la cuerda l-x que está sobre la mesa se anula con la reacción de la misma.
Sean F_x y F_y las componentes de la fuerza que ejerce el borde de la mesa sobre la cuerda para que mantenga en todo momento, la forma de "L invertida”.

La segunda ley de Newton a lo largo del eje X y del eje Y, respectivamente, se escribe.

$\begin{array}{l} F_{x} = \frac{d p_{x}}{d t} F_{x} = - ρ (l - x) \frac{d^{2} x}{d t^{2}} + ρ {(\frac{d x}{d t})}^{2} \\ F_{y} + ρ g x = \frac{d p_{y}}{d t} F_{y} = - ρ g x + ρ {(\frac{d x}{d t})}^{2} + ρ x \frac{d^{2} x}{d t^{2}} \end{array}$

En la ecuación del movimiento, despejamos la aceleración d²x/dt² y en la ecuación de la conservación de la energía despejamos la velocidad dx/dt..

$\frac{d^{2} x}{d t^{2}} = \frac{g}{l} x {(\frac{d x}{d t})}^{2} = \frac{g}{l} (x^{2} - x_{0}^{2})$

Expresando F_x y F_y en función de x.

$F_{x} = F_{y} = \frac{ρ g}{l} (2 x^{2} - x l - x_{0}^{2})$

Cuando t=0, la cuerda empieza a moverse, x=x₀, F_x>0 está dirigida hacia fuera de la mesa
Cuando x=l, la cuerda abandona la mesa, F_x<0, la fuerza es negativa.

Para una x determinada se cumple que F_x=0

$x = \frac{l + \sqrt{l^{2} + 8 x_{0}^{2}}}{4}$

Actividades

Se introduce

La longitud de la parte de la cuerda x₀ que cuelga del bode de la mesa en el instante inicial t=0, actuando en la barra de desplazamiento titulada Cuerda que cuelga
La longitud de la cuerda se ha fijado en l=1 m

Se pulsa el botón titulado Empieza

Se observa el movimiento de la cuerda.

Se proporciona los datos de x (longitud de la parte de la cuerda que cuelga del borde de la mesa), la velocidad de la cuerda v, en cada instante t.

Se dibujan mediante flechas, las fuerzas exteriores que actúan sobre el sistema (con la excepción del peso de la parte de la cuerda que está sobre la mesa, y la reacción de ésta, que se anulan). Se proporciona el valor de la fuerza F_x=F_y que hay que ejercer sobre la cuerda en el borde de la mesa para que mantenga en todo momento la forma de “L invertida”.

En la parte izquierda del applet, un diagrama de barras nos muestra los cambios energéticos.

La energía potencial (negativa) se representa por una barra vertical de color azul (por debajo del origen)
La energía cinética (positiva) se representa por una barra vertical de color rojo (por encima del origen).

Referencias

Prato D., Gleiser R., Another look at the uniform rope sliding over the edge of a smoooth table. Am. J. Phys. 50 (6) June 1982, pp. 536-539.

Vrbik J. Chain sliding off a table. Am. J. Physics 61 (3) March 1993, pp. 258-261.