Caída de una cadena que cuelga de un clavo.

El movimiento de la cadena que pende de un clavo tiene dos etapas. La primera, mientras la cadena está en contacto con el clavo. La segunda, cuando deja de estar en contacto. En esta etapa, consideraremos la cadena como un sistema de dos partículas en caída libre. Sistema que se ha estudiado en otras páginas de este capítulo, pero en este caso desconocemos la fuerza de interacción entre las dos partículas

En ambos casos, supondremos que la energía de la cadena se mantiene constante.

Primera etapa del movimiento

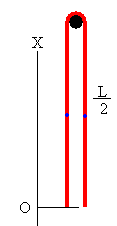
Supongamos una cadena de masa ρ por unidad de longitud, de longitud L suspendida de un clavo clavado en una pared.

Situamos el origen en la posición de los extremos de la cadena cuando está en equilibrio inestable, tal como se muestra en la figura de la izquierda.

Principio de conservación de la energía

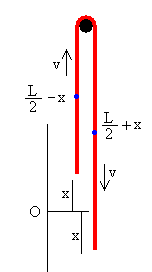
Los centros de masa (señalados mediante puntos de color azul) de ambas partes de la cadena se encuentran a una altura L/4. La energía inicial de la cadena en la posición inicial en reposo es

$E = (ρ \frac{L}{2}) g \frac{L}{4} + (ρ \frac{L}{2}) g \frac{L}{4} = ρ g \frac{L^{2}}{4}$

La cadena se mueve, en un instante dado t, cuando los extremos se desplazan x, la energía de la cadena es

$\begin{array}{l} E = \frac{1}{2} ρ L {(\frac{d x}{d t})}^{2} + ρ (\frac{L}{2} - x) g (x + \frac{L}{4} - \frac{x}{2}) + ρ (\frac{L}{2} + x) g (\frac{L}{4} + \frac{x}{2} - x) = \\ \frac{1}{2} ρ L {(\frac{d x}{d t})}^{2} + ρ g (\frac{L^{2}}{4} - x^{2}) \end{array}$

Aplicamos el principio de conservación de la energía y despejamos la velocidad de la cadena

$\frac{d x}{d t} = \sqrt{\frac{2 g}{L}} x$

Ecuaciones del movimiento

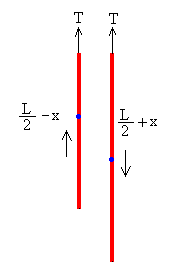
Las fuerzas sobre la parte izquierda de la cadena son:

El peso ρ(L/2-x)g
La tensión T de la cadena en la parte superior

La ecuación del movimiento de esta parte de la cadena es

$ρ (\frac{L}{2} - x) \frac{d^{2} x}{d t^{2}} = T - ρ (\frac{L}{2} - x) g$

Las fuerzas sobre la parte derecha de la cadena son:

El peso ρ(L/2+x)g
La tensión T de la cadena en la parte superior

La ecuación del movimiento de esta porción es

$ρ (\frac{L}{2} + x) \frac{d^{2} x}{d t^{2}} = ρ (\frac{L}{2} + x) g - T$

Eliminamos la fuerza desconocida T sumando ambas ecuaciones

$ρ L \frac{d^{2} x}{d t^{2}} = 2 ρ g x \frac{d^{2} x}{d t^{2}} - \frac{2 g}{L} x = 0$

Las raíces de la ecuación característica son reales. La solución de esta ecuación diferencial es

$x = A \exp (r t) + B \exp (- r t) r = \sqrt{\frac{2 g}{L}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales

Si la cadena se coloca en su posición de equilibrio inestable, permanecerá así, hasta que alguna perturbación haga que un extremo se eleve x₀ y el otro baje x₀. Las condiciones iniciales que vamos a establecer son las siguientes:

En el instante t=0, los extremos de la cadena se encuentran desplazados x₀, y la velocidad de la cadena v₀ es

$v_{0} = \sqrt{\frac{2 g}{L}} x_{0}$

Fácilmente, podemos comprobar que los coeficientes A=x₀ y B=0. La ecuación del movimiento de la cadena es

$x = x_{0} \exp (\sqrt{\frac{2 g}{L}} t) v = \frac{d x}{d t} = \sqrt{\frac{2 g}{L}} x$

tal como habíamos obtenido, aplicando el principio de conservación de la energía.

Fuerza que ejerce el clavo sobre la cadena

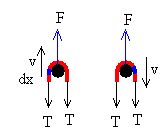El clavo hace doblar la cadena, de modo que en un intervalo de tiempo comprendido entre t y t+dt, una porción dx de la cadena (en color azul) pasa de la parte izquierda hacia la parte derecha. Un elemento de masa ρ·dx cambia su momento lineal de (ρ·dx)·v a (ρ·dx)(-v).

El momento lineal del elemento de masa cambia dp=-2(ρ·dx)v en el intervalo de tiempo dt. La fuerza necesaria para realizar este cambio de momento lineal es

$\frac{d p}{d t} = - 2 ρ v \frac{d x}{d t} = - 2 ρ v^{2}$

Las fuerzas sobre la porción de cadena que está sobre el clavo son:

la fuerza F que ejerce el clavo
la tensión T que ejerce la parte izquierda de la cadena sobre dicha porción
la tensión T que ejerce la parte derecha sobre dicha porción

F-2T=-2ρv²

Calculamos T restando las ecuaciones del movimiento de cada una de las dos partes de la cadena.

$2 T = ρ L g - 2 ρ x \frac{d^{2} x}{d t^{2}}$

Introduciendo los valores de la aceleración d²x/dt² y de la velocidad v=dx/dt, calculamos la fuerza F

$F = ρ L g - 8 ρ g \frac{x^{2}}{L}$

La fuerza F que ejerce el clavo se hace cero cuando los extremos de la cadena se han desplazado

$x = \frac{L}{2 \sqrt{2}}$

A partir de este momento, la cadena cae libremente, bajo la aceleración constante de la gravedad.

Final de la primera etapa del movimiento y comienzo de la segunda

La primera etapa del movimiento finaliza en el instante t₁ tal que

$\frac{L}{2 \sqrt{2}} = x_{0} \exp (\sqrt{\frac{2 g}{L}} t_{1}) t_{1} = \sqrt{\frac{L}{2 g}} \ln (\frac{L}{2 \sqrt{2} x_{0}})$

Las velocidades finales de cada una de las dos partes de la cadena son

$v = \sqrt{\frac{2 g}{L}} \frac{L}{2 \sqrt{2}} = \frac{1}{2} \sqrt{g L}$

La posición del centro de masas es

$x_{c m} = \frac{ρ (\frac{L}{2} - x) (x + \frac{L}{4} - \frac{x}{2}) + ρ (\frac{L}{2} + x) (\frac{L}{4} + \frac{x}{2} - x)}{ρ L} = \frac{L}{4} - \frac{x^{2}}{L}$

Al finalizar la primera etapa, el centro de masa se encuentra en la posición x_cm=L/8

La velocidad del centro de masas es

$v_{c m} = \frac{ρ (\frac{L}{2} - x) v + ρ (\frac{L}{2} + x) (- v)}{ρ L} = \frac{- 2 x v}{L} = - 2 \frac{x^{2}}{L} \sqrt{\frac{2 g}{L}}$

Al finalizar la primera etapa, la velocidad del centro de masa es

$v_{c m} = - \frac{1}{2} \sqrt{\frac{g L}{2}}$

La energía total de la cadena se mantiene constante e igual a la energía inicial

$E = ρ g \frac{L^{2}}{4}$

Segunda etapa del movimiento

En esta etapa del movimiento, consideramos un sistema de dos partículas que se mueven bajo la acción de la aceleración de la gravedad y la fuerza de interacción mutua que es desconocida.

Movimiento del centro de masas de la cadena

El centro de masas de la cadena se mueve como una partícula de masa mL bajo la acción de la única fuerza externa, que es su propio peso.

Sabiendo que la posición inicial y la velocidad inicial del c.m. al comenzar esta etapa del movimiento son

$x_{c m} = \frac{L}{8} v_{c m} = - \frac{1}{2} \sqrt{\frac{g L}{2}}$

La velocidad y la posición del c.m. de la cadena en función del tiempo t (se pone el reloj a cero al comienzo de la segunda etapa) son

$v_{c m} = - \frac{1}{2} \sqrt{\frac{g L}{2}} - g t x_{c m} = \frac{L}{8} - \frac{1}{2} \sqrt{\frac{g L}{2}} t - \frac{1}{2} g t^{2}$

Movimiento de cada una de las dos partes de la cadena

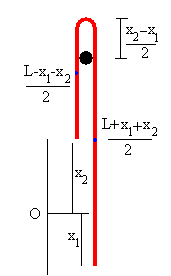
Para determinar el movimiento de cada partícula, en vez de formular las ecuaciones del movimiento, ya que la fuerza de interacción mutua es desconocida, emplearemos el principio de conservación de la energía.

En el instante t, el extremo izquierdo de la cadena se ha desplazado x₂ y el extremo derecho se ha desplazado x₁.

La posición del centro de masas x_cm, en función de x₂ y x_1, es

$\begin{array}{l} x_{c m} = \frac{ρ (\frac{L - x_{1} - x_{2}}{2}) (x_{2} + \frac{L - x_{1} - x_{2}}{4}) + ρ (\frac{L + x_{1} + x_{2}}{2}) (\frac{L + x_{1} + x_{2}}{4} - x_{1})}{ρ L} = \\ = \frac{L}{4} + \frac{1}{2} (x_{2} - x_{1}) - \frac{1}{4 L} {(x_{2} + x_{1})}^{2} \end{array}$

La velocidad del centro de masas v_cm se expresa en función de la velocidad del c.m. de cada una de las dos partes de la cadena v₁=dx₁/dt y v₂=dx₂/dt.

$v_{c m} = \frac{ρ (\frac{L - x_{1} - x_{2}}{2}) v_{2} + ρ (\frac{L + x_{1} + x_{2}}{2}) (- v_{1})}{ρ L} = \frac{1}{2} (v_{2} - v_{1}) - \frac{1}{2 L} (x_{2} + x_{1}) (v_{2} + v_{1})$

Podemos verificar que la velocidad del c.m. se obtiene derivando la posición del c.m., v_cm=dx_cm/dt

Energía del sistema de partículas

La energía cinética de un sistema de dos partículas es igual a la energía cinética del centro de masas más la energía cinética de las dos partículas referida al c.m.

Calculamos las velocidades relativas de cada una de las dos partes de la cadena respecto del centro de masas.

$\begin{array}{l} v_{2 c m} = v_{2} - v_{c m} = \frac{1}{2} (v_{1} + v_{2}) + \frac{1}{2 L} (x_{2} + x_{1}) (v_{2} + v_{1}) \\ v_{1 c m} = - v_{1} - v_{c m} = - \frac{1}{2} (v_{1} + v_{2}) + \frac{1}{2 L} (x_{2} + x_{1}) (v_{2} + v_{1}) \end{array}$

La energía cinética de la cadena es

$\begin{array}{l} E_{k} = \frac{1}{2} ρ L v_{c m}^{2} + \frac{1}{2} ρ (\frac{L - x_{1} - x_{2}}{2}) v_{2 c m}^{2} + \frac{1}{2} ρ (\frac{L + x_{1} + x_{2}}{2}) v_{1 c m}^{2} = \\ \frac{1}{2} ρ L v_{c m}^{2} + \frac{1}{8} ρ L ({(v_{1} + v_{2})}^{2} - \frac{{(x_{1} + x_{2})}^{2} {(v_{1} + v_{2})}^{2}}{L^{2}}) \end{array}$

La energía potencial del sistema de dos partículas es la energía potencial de su centro de masas

E_p=(ρL)gx_cm

La energía total permanece constante e igual a la energía inicial

$E_{k} + E_{p} = \frac{1}{4} ρ g L^{2}$

Introducimos las expresiones de la velocidad v_cm y posición del c.m. x_cm del centro de masas en función del tiempo t.

$\begin{array}{l} \frac{1}{2} ρ L {(- \frac{1}{2} \sqrt{\frac{g L}{2}} - g t)}^{2} + \frac{1}{8} ρ L ({(v_{1} + v_{2})}^{2} - \frac{{(x_{1} + x_{2})}^{2} {(v_{1} + v_{2})}^{2}}{L^{2}}) + \\ ρ L g (\frac{L}{8} - \frac{1}{2} \sqrt{\frac{g L}{2}} t - \frac{1}{2} g t^{2}) = \frac{1}{4} ρ g L^{2} \end{array}$

Después de simplificar, obtenemos la ecuación

${(v_{1} + v_{2})}^{2} - \frac{{(x_{1} + x_{2})}^{2} {(v_{1} + v_{2})}^{2}}{L^{2}} = \frac{1}{2} g L$

Llamando z=x₁+x₂ y v=dz/dt=v₁+v₂, obtenemos la ecuación diferencial

$\sqrt{L^{2} - z^{2}} \frac{d z}{d t} = \sqrt{\frac{g L^{3}}{2}}$

Haciendo el cambio de variable z=L·sinθ e integrando

$\int_{θ_{0}}^{θ} L^{2} \cos^{2} θ \cdot d θ = \int_{0}^{t} \sqrt{\frac{g L^{3}}{2}} d t$

En el instante t=0, comienzo de la segunda etapa del movimiento

$z_{0} = x_{1} + x_{2} = 2 \frac{L}{2 \sqrt{2}} = \frac{L}{\sqrt{2}}$

El límite inferior de la integral es θ₀=π/4

Se calcula la integral de cos²θ por partes o a través de la relación trigonométrica cos²θ=(1+cos2θ)/2. El resultado es

$θ + \frac{1}{2} \sin (2 θ) - \frac{π}{4} - \frac{1}{2} = \sqrt{\frac{2 g}{L}} t$

Dado el valor de t, se resuelve esta ecuación trascendente por el procedimiento del punto medio y se calcula el ángulo θ y después, z=x₁+x₂=L·sinθ

Obtenemos los desplazamientos x₁ y x₂ de los extremos derecho e izquierdo de la cadena, a partir de el conocimiento de z en función del tiempo t y de la posición x_cm del centro de masa en función del tiempo t.

$\begin{array}{l} z = x_{1} + x_{2} \\ x_{c m} = \frac{L}{4} + \frac{1}{2} (x_{2} - x_{1}) - \frac{1}{4 L} {(x_{2} + x_{1})}^{2} = \frac{L}{4} + \frac{1}{2} (x_{2} - x_{1}) - \frac{1}{4 L} z^{2} \end{array}$

Despejamos x₁ y x₂ en función de z y x_cm

$\begin{array}{l} x_{1} = \frac{z}{2} - x_{c m} + \frac{L}{4} - \frac{z^{2}}{4 L} \\ x_{2} = \frac{z}{2} + x_{c m} - \frac{L}{4} + \frac{z^{2}}{4 L} \end{array}$

Despejamos las velocidades v₁ y v₂ de cada una de las dos partes de la cadena a partir de la velocidad v_cm del centro de masas y la derivada de z respecto del tiempo, v=dz/dt.

$\begin{array}{l} v = v_{1} + v_{2} \\ v_{c m} = \frac{1}{2} (v_{2} - v_{1}) - \frac{1}{2 L} (x_{2} + x_{1}) (v_{2} + v_{1}) = \frac{1}{2} (v_{2} - v_{1}) - \frac{1}{2 L} z v \end{array}$

Despejando v₁ y v₂ del sistema de dos ecuaciones

$v_{1} = - v_{c m} + \frac{1}{2} (1 - \frac{z}{L}) v v_{2} = v_{c m} + \frac{1}{2} (1 + \frac{z}{L}) v$

Final de la segunda etapa del movimiento

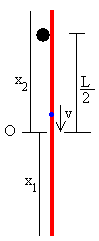La segunda etapa finaliza, cuando la parte izquierda de la cadena ha desaparecido, y toda la cadena está en la parte derecha, entonces z=x₁+x₂=L.

Cuando z=L, el ángulo θ=π/2 y se despeja el tiempo t₂ de la ecuación trascendente

$t_{2} = \sqrt{\frac{L}{2 g}} (\frac{π}{4} - \frac{1}{2})$

La posición final del centro de masas es

$x_{c m} = \frac{L}{8} - \frac{1}{2} \sqrt{\frac{g L}{2}} t_{2} - \frac{1}{2} g t_{2}^{2} = \frac{L}{16} (3 - \frac{π^{2}}{4})$

Los desplazamientos finales de los extremos de la cadena son

$\begin{array}{l} x_{1} = \frac{z}{2} - x_{c m} + \frac{L}{4} - \frac{z^{2}}{4 L} = \frac{L}{16} (5 + \frac{π^{2}}{4}) \\ x_{2} = \frac{z}{2} + x_{c m} - \frac{L}{4} + \frac{z^{2}}{4 L} = \frac{L}{16} (11 - \frac{π^{2}}{4}) \end{array}$

Comprobamos que x₁+x₂=L

El extremo izquierdo se encuentra por encima de el clavo

$x_{2} - \frac{L}{2} = 0.033 \cdot L$

Calculamos ahora, la velocidad final de cada una de las dos partes de la cadena

La velocidad final del centro de masas es

$v_{c m} = - \frac{1}{2} \sqrt{\frac{g L}{2}} - g t_{2} = - \frac{π}{4} \sqrt{\frac{g L}{2}}$

Al finalizar esta segunda etapa z=L, la velocidad de la parte derecha de la cadena tiene el valor

$v_{1} = - v_{c m} + \frac{1}{2} (1 - \frac{z}{L}) v = - \frac{π}{4} \sqrt{\frac{g L}{2}}$

Como v=dz/dt tiende a infinito cuando z tiende a L. La longitud (y la masa) de la parte izquierda de la cadena tienden a cero a la vez, que su velocidad tiende a infinito.

Actividades

La cadena tiene una densidad lineal ρ=1, y una longitud L=1.

Los extremos de la cadena se desplazan x₀=0.01 y se les proporciona una velocidad inicial.

$v_{0} = \sqrt{2 \cdot 9.8} x_{0}$

Se pulsa el botón titulado Empieza

Observamos

Los desplazamientos x₁ y x₂ de los extremos derecho e izquierdo de la cadena.
La fuerza F que ejerce el clavo durante la primera etapa del movimiento mediante una flecha de color azul.
La posición del centro de masa x_cm, un punto de color azul
En la parte derecha del applet, un diagrama de tarta dividido en cuatro sectores, representa la energía potencial y cinética de cada una de las dos partes de la cadena.

En la parte superior del applet, se proporcionan los valores numéricos de:

El desplazamiento del extremo izquierdo de la cadena, xIzq
El desplazamiento del extremo derecho de la cadena, xDcha
La velocidad del c.m. de la parte izquierda, vIzq
La velocidad del c.m. de la parte derecha, vDcha
La energía total constante de la cadena

Referencias

Calkin M. G., The dynamics of a falling chain: II. Am. J. Phys. 57 (2) February 1989, pp. 157-159.