• Inicio
• Dinámica
• Sistemas de masa variable

Estudio del movimiento de una cadena con una máquina de Atwood

En esta página, se continua el estudio del movimiento de una cadena apilada sobre el suelo, uno de cuyos extremos cuelga de un hilo fino que pasa por una polea. El otro extremo del hilo está unido a un cuerpo, tal como se muestra en la figura.

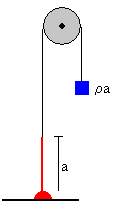
El peso del cuerpo es igual al peso ρa de una longitud a de la cadena. Donde ρ es la masa por unidad de longitud de la cadena.

Por tanto, el extremo de la cadena unido al hilo se eleva una longitud x=a para que se equilibre con el peso del cuerpo en una máquina de Atwood, tal como se muestra en la figura.

En la situación inicial, la cadena está completamente apilada en el suelo, x=0, y la velocidad inicial v=0. El bloque tira de la cadena que se eleva hasta que alcanza una altura máxima. Analizamos el movimiento de la cadena cuando su extremo se ha elevado una altura x, tal como se muestra en la figura

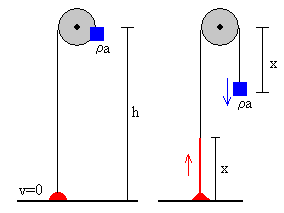
Movimiento de la cadena hacia arriba.

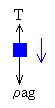
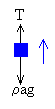
Las fuerzas sobre el cuerpo son:

• El peso del cuerpo, ρag

• La tensión del hilo, T.

La ecuación del movimiento es

${\displaystyle \rho ag-T=\rho a\frac{dv}{dt}}$

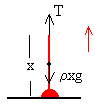Las fuerzas sobre la cadena son:

• El peso de la longitud x de la cadena, ρxg, que actúa en el centro de masas

• La tensión del hilo T, que es la misma a ambos lados de la polea si se considera que tiene una masa despreciable.

Empleamos la definición de fuerza F=dp/dt, donde p es el momento lineal de la cadena, para escribir la ecuación de su movimiento

${\displaystyle T-\rho xg=\frac{d(\rho xv)}{dt}T-\rho xg=\rho x\frac{dv}{dt}+\rho v^2}$

Eliminamos T del sistema de dos ecuaciones

${\displaystyle (a+x)\frac{dv}{dt}=g(a-x)-v^2}$                 (1)

Expresamos v en función de la altura x del extremo de la cadena en vez del tiempo t.

${\displaystyle \frac{dv}{dt}=\frac{dx}{dt}\frac{dv}{dx}=v\frac{dv}{dx}=\frac{1}{2}\frac{d{v}^2}{dx}}$

y multiplicamos la ecuación diferencial por (a+x), resultando

${\displaystyle {\left(a+x\right)}^2\frac{d{v}^2}{dx}+2v^2(a+x)=2g(a-x)(a+x)}$

Haciendo el cambio de variable z²=(a+x)²·v²

${\displaystyle \frac{d{z}^2}{dx}=2g(a-x)(a+x)}$

Integrando

${\displaystyle \begin{array}{l}{\displaystyle \underset{z_0}{\overset{z}{\int }}d{z}^2}={\displaystyle \underset{x_0}{\overset{x}{\int }}2g(a^2-x^2)}dx\\ z^2-z_0^2=2g\left(a^{2}x-\frac{x^3}{3}\right)-2g\left(a^2{x}_0-\frac{x_0^3}{3}\right)\end{array}}$

Deshaciendo el cambio

${\displaystyle v^2{\left(a+x\right)}^2-v_0^2{\left(a+x_0\right)}^2=2g\left(a^{2}x-\frac{x^3}{3}\right)-2g\left(a^2{x}_0-\frac{x_0^3}{3}\right)}$

Si partimos de la posición inicial x₀=0 con velocidad inicial v₀=0.

${\displaystyle v^2{\left(a+x\right)}^2=2g\left(a^{2}x-\frac{x^3}{3}\right)}$

El extremo de la cadena se mueve hacia arriba, el cuerpo se mueve hacia abajo con la misma velocidad, hasta que se detienen v=0, en la posición

${\displaystyle x_u=a\sqrt{3}}$

Ecuación del movimiento (v>0)

Para calcular la posición del extremo de la cadena en función del tiempo, resolvemos mediante procedimientos numéricos la ecuación diferencial del movimiento (1)

${\displaystyle \frac{d^{2}x}{d{t}^2}=\frac{1}{a+x}\left(g(a-x)-{\left(\frac{dx}{dt}\right)}^2\right)}$

con las condiciones iniciales t=0, x=0, dx/dt=0.

Movimiento de la cadena hacia abajo.

La ecuación del movimiento del cuerpo (v<0) es

${\displaystyle \rho ag-T=\rho a\frac{dv}{dt}}$

De acuerdo con el artículo mencionado en las referencias, durante el movimiento de la cadena hacia abajo, el suelo ha de actuar con una fuerza suficiente para detener el movimiento de los eslabones de la cadena que lo golpean.

En un intervalo de tiempo dt, una masa dm de la cadena cuya velocidad es v, choca inelásticamente contra el suelo y se detiene completamente. Esta disminución de momento lineal v·dm de la cadena en el tiempo dt, se debe a su interacción con el suelo, que podemos describir mediante una fuerza hacia arriba F_s= vdm/dt=ρv²

En el apartado "Fuerza que ejerce el suelo sobre la cadena que cae" se pone un ejemplo.

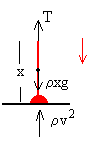La ecuación del movimiento de la cadena hacia abajo (v<0) será

${\displaystyle T-\rho xg+\rho v^2=\frac{d(\rho xv)}{dt}T-\rho xg+\rho v^2=\rho x\frac{dv}{dt}+\rho v^2}$

Eliminamos T del sistema de dos ecuaciones

${\displaystyle (a+x)\frac{dv}{dt}=g(a-x)}$           (2)

Expresamos v en función de la longitud x de la cadena en vez del tiempo t, como en el apartado Movimiento de la cadena hacia arriba.

${\displaystyle \frac{d{v}^2}{dx}=\frac{2g(a-x)}{(a+x)}}$

Integramos con la condición de que en la posición x₀, v=v₀

${\displaystyle {\displaystyle \underset{v_0}{\overset{v}{\int }}d{v}^2}={\displaystyle \underset{x_0}{\overset{x}{\int }}2g\left(\frac{2a}{a+x}-1\right)}dx}$

La integral es inmediata

${\displaystyle v^2-v_0^2=2g\left(2a\ln \frac{a+x}{a+x_0}-x+x_0\right)}$

En el movimiento hacia abajo, parte de la posición inicial $x_0=a\sqrt{3}$  con velocidad v₀=0.

${\displaystyle v^2=2g\left(2a\ln \frac{a+x}{a+a\sqrt{3}}-x+a\sqrt{3}\right)}$

La velocidad se hace nula v=0 en la posición x_d=0.412·a, que se obtiene resolviendo la ecuación trascendente

${\displaystyle 2\ln \frac{1+z}{1+\sqrt{3}}-z+\sqrt{3}=0z=\frac{x}{a}}$

Ecuación del movimiento (v<0)

Para calcular la posición del extremo de la cadena en función del tiempo, resolvemos mediante procedimientos numéricos la ecuación diferencial del movimiento (2)

${\displaystyle \frac{d^{2}x}{d{t}^2}=g\frac{a-x}{a+x}}$

con las condiciones iniciales t=t₀, $x_0=a\sqrt{3}$ , dx/dt=0.

Balance energético

Para efectuar el balance energético, comparamos la situación inicial y la final, cuando el extremo de la cadena se ha elevado una altura x, tal como se muestra en la figura.

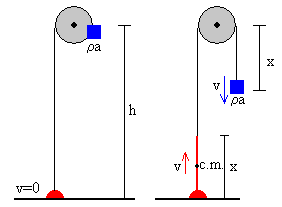
La energía inicial cuando el extremo de la cadena está en el suelo x=0, y el cuerpo está a una altura h sobre el suelo es

E₀=ρagh

Cuando el extremo de la cadena asciende una altura x.

• La energía potencial del cuerpo es ρag(h-x)

• La energía potencial del centro de masa de la cadena es $\rho xg\frac{x}{2}=\frac{1}{2}\rho x^{2}g$

• La energía cinética del cuerpo es $\frac{1}{2}\rho a{v}^2$

• La energía cinética de la cadena es $\frac{1}{2}\rho x{v}^2$

La energía final, es la suma de las cuatro contribuciones

${\displaystyle E=\rho ag(h-x)+\rho g\frac{x^2}{2}+\frac{1}{2}\rho a{v}^2+\frac{1}{2}\rho x{v}^2}$

La razón del cambio de energía E con el tiempo t es

${\displaystyle \frac{dE}{dt}=-\rho gav+\rho gxv+\rho (a+x)v\frac{dv}{dt}+\frac{1}{2}\rho v^3}$

• En el movimiento hacia arriba tenemos que (1)

${\displaystyle (a+x)\frac{dv}{dt}=g(a-x)-v^2}$

Simplificando llegamos a la expresión

${\displaystyle \frac{dE}{dt}=-\frac{1}{2}\rho v^3}$

La energía total del sistema disminuye con el tiempo en proporción al cubo de la velocidad.

• En el movimiento hacia abajo (2)

${\displaystyle (a+x)\frac{dv}{dt}=g(a-x)}$

por lo que

${\displaystyle \frac{dE}{dt}=\frac{1}{2}\rho v^3}$

Como en el movimiento hacia abajo v<0. La energía E del sistema disminuye del mismo modo en el movimiento hacia arriba.

Calculamos la variación de energía en el movimiento hacia arriba desde x=0 (posición inicial de partida) hasta $x_u=a\sqrt{3}$ . En ambas posiciones la velocidad v=0.

${\displaystyle \Delta E=E-E_0=\rho g\frac{x_u^2}{2}+\rho ag(h-x_u)-\rho agh=\rho g\left(\frac{3}{2}-\sqrt{3}\right)a^2=-0.23\rho g{a}^2}$

Calculamos la variación de energía en el movimiento hacia abajo desde la posición $x_u=a\sqrt{3}$  hasta la posición x_d=0.412·a.

${\displaystyle \Delta E=\rho g\frac{x_d^2}{2}+\rho ag(h-x_d)-\rho g\frac{x_u^2}{2}-\rho ag(h-x_u)=-0.095\rho g{a}^2}$

Sucesivas posiciones del extremo de la cadena para las cuales v=0

• Movimiento hacia arriba

La velocidad del cuerpo y del extremo de la cadena viene dada por la ecuación

${\displaystyle v^2{\left(a+x\right)}^2-v_0^2{\left(a+x_0\right)}^2=2g\left(a^{2}x-\frac{x^3}{3}\right)-2g\left(a^2{x}_0-\frac{x_0^3}{3}\right)}$

Como la velocidad v₀=0 en la posición inicial x₀=x_d y v=0 en la posición final x=x_u. Conocida x_d se calcula x_u resolviendo la ecuación cúbica por el procedimiento del punto medio.

${\displaystyle \left(a^{2}x-\frac{x^3}{3}\right)-\left(a^2{x}_d-\frac{x_d^3}{3}\right)=\text{0}z-\frac{z^3}{3}-z_0+\frac{z_0^3}{3}=0}$

con z=x/a y z₀=x_d/a

Por ejemplo, el extremo de la cadena parte del reposo v₀=0 en la posición inicial x_d=0, se mueve hacia arriba hasta que alcanza la posición $x_u=a\sqrt{3}$

• Movimiento hacia abajo

La velocidad del bloque, durante el movimiento hacia abajo del extremo de la cadena viene dada por la ecuación

${\displaystyle v^2-v_0^2=2g\left(2a\ln \frac{a+x}{a+x_0}-x+x_0\right)}$

Como la velocidad v₀=0 en la posición inicial x₀=x_u y v=0 en la posición final x=x_d. Conocida x_u se calcula x_d resolviendo la ecuación trascendente.

${\displaystyle 2a\ln \frac{a+x}{a+x_u}-x+x_u=02\ln \frac{1+z}{1+z_0}-z+z_0=0}$

con z=x/a y z₀=x_u/a

Por ejemplo, el extremo de la cadena parte del reposo en la posición inicial $x_u=a\sqrt{3}$  y se mueve hacia abajo hasta que alcanza la posición x_d=0.412·a.

En la tabla y en la gráfica, se recogen los datos de las sucesivas posiciones x_d/a y x_u/a del extremo de la cadena para las cuales su velocidad v=0.

xd/a xu/a 0.0 1.732 0.412 1.489 0.580 1.368 0.673 1.295 0.732 1.246 0.773 1.211 0.803 1.185 0.826 1.165 0.844 1.149

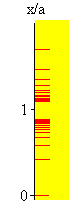Las dos sucesiones convergen lentamente hacia el valor 1 que es la situación de equilibrio de un cuerpo cuya masa es igual a la de una porción de longitud a de la cadena (véase la figura al principio de la página).

Actividades

Se introduce

• El valor de la masa del bloque, igual a una porción de longitud a de la cadena, actuando la barra de desplazamiento titulada Masa cuerpo/cadena.

• La densidad lineal m o masa por unidad de longitud de la cadena se ha fijado en el valor ρ=1

Se pulsa el botón titulado Empieza

Se observa el movimiento del cuerpo y de la cadena hacia arriba y hacia abajo.

Sobre la regla situada a la izquierda del applet, se señalan las sucesivas posiciones del extremo de la cadena para las cuales la velocidad es nula (v=0).

En la parte derecha del applet, un diagrama en forma de tarta, nos muestra la energía del sistema formado por el cuerpo y la cadena, dividido en sectores

• La energía potencial del cuerpo, en color azul

• la energía potencial del centro de masa de la cadena, en color rojo

• La energía cinética del cuerpo, en color azul claro

• La energía cinética de la parte de la cadena que cuelga, en color rosa

• La energía que se va perdiendo en el movimiento hacia arriba y hacia abajo de la cadena, en color negro

Fuerza que ejerce el suelo sobre la cadena que cae

Para entender el origen de la fuerza que ejerce el suelo sobre una cadena que cae, resolvemos primero el siguiente problema.

Una ametralladora dispara 600 balas de 40 g cada minuto, con una velocidad de 500 m/s. Calcular la fuerza media con la que se debe sujetar la ametralladora.

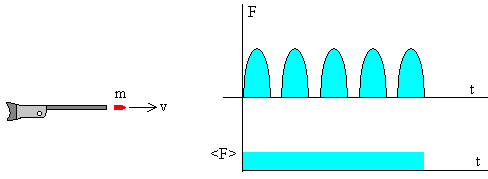
En la parte de arriba, se muestra la fuerza instantánea que ejerce la ametralladora al disparar cada una de las balas. La fuerza crece rápidamente pero dura muy poco tiempo. En la parte inferior, se muestra la fuerza media <F> que ejerce la ametralladora al disparar sucesivamente N balas.

Para cada una de las balas la variación de momento lineal es igual al impulso (área bajo cada una de las curvas)

${\displaystyle mv={\displaystyle \int F·dt}}$

Cuando se disparan N balas, el cambio de momento total es igual al impulso total

${\displaystyle N·mv=N{\displaystyle \int F·dt}=<F>·t}$

Despejando la fuerza media <F>

${\displaystyle <F>=\frac{N}{t}mv<F>=\frac{600}{60}0.04·500=200\text{N}}$

Consideremos ahora el caso de una cadena con eslabones muy pequeños (aproximación continua). La cadena tiene una masa ρ por unidad de longitud. Supongamos que en el instante t la velocidad de la cadena es v.

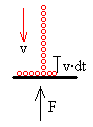
En el intervalo de tiempo entre t y t+dt, una masa ρ·v·dt choca con el suelo con velocidad v. Si después del choque la cadena permanece apilada en reposo, el cambio de momento lineal es dp=(ρ·v·dt)·v. El impulso de la fuerza F que ejerce el suelo es F·dt.

Como F·dt=dp entonces F=ρv²

Referencias

Davis A. Error in the vibrating chain problem. Am. J. Phys. 20 (2) February 1952, pp. 112-114

Curso Interactivo de Física en Internet © Ángel Franco García