• Inicio
• Electromagnetismo
• Campo eléctrico

Modelo atómico de Kelvin-Thomson

Actualmente, los libros de texto no suelen mencionar el átomo de Kelvin-Thomson. Sin embargo, durante el periodo que va de 1902 a1906 tuvo bastante éxito, hasta que Rutherford demostró que este modelo no podía explicar la dispersión de las partículas alfa por los átomos de una lámina de oro.

Este modelo simple de átomo explicaba bastante bien la valencia química, la emisión de partículas β por los núcleos de elementos radioactivos, etc.

El aspecto didáctico más importante es la aplicación de la ley de Gauss a una distribución esférica y uniforme de carga, y describir el movimiento oscilatorio de los electrones en dicho átomo.

Consideramos el caso más simple, un átomo o ion hidrogenoide con un solo electrón. Suponemos que el átomo tiene forma esférica de radio R, y que la carga positiva Q está uniformemente distribuida en dicha esfera.

Campo eléctrico de una distribución esférica y uniforme de carga

El teorema de Gauss afirma que el flujo del campo eléctrico a través de una superficie cerrada es igual al cociente entre la carga en el interior de dicha superficie dividido entre ε₀.

${\displaystyle {\displaystyle \oint E\cdot dS}=\frac{q}{{\epsilon }_0}}$

Para una distribución esférica y uniforme de carga, la aplicación del teorema de Gauss requiere los siguientes pasos:

1.-A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.

La distribución de carga tiene simetría esférica, la dirección del campo es radial

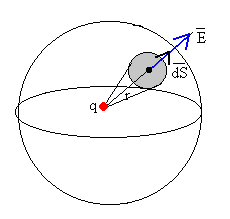2.-Elegir una superficie cerrada apropiada para calcular el flujo

Tomamos como superficie cerrada, una esfera de radio r.

El campo eléctrico E es paralelo al vector superficie dS, y el campo es constante en todos los puntos de la superficie esférica como se ve en la figura, por lo que,

${\displaystyle {\displaystyle \underset{S}{\int }E·dS}={\displaystyle \underset{S}{\int }EdS\cos 0º}=E{\displaystyle \underset{S}{\int }dS}=E4\pi r^2}$

El flujo total es,  E·4πr²

 

3. Determinar la carga que hay en el interior de la superficie cerrada

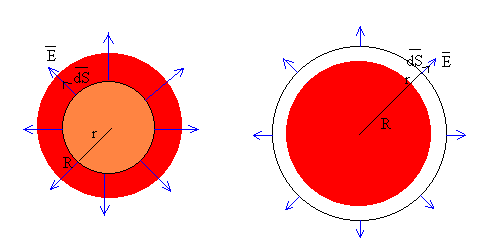
• Para r<R. (figura de la izquierda)

Si estamos calculando el campo en el interior de la esfera uniformemente cargada, la carga que hay en el interior de la superficie esférica de radio r es una parte de la carga total (en color rosado), que se calcula multiplicando la densidad de carga por el volumen de la esfera de radio r.

${\displaystyle q=Q\frac{r^3}{R^3}}$

• Para r>R (figura de la derecha)

Si estamos calculando el campo en el exterior de la esfera uniformemente cargada, la carga que hay en el interior de la superficie esférica de radio r es la carga total q=Q.

4.-Aplicar el teorema de Gauss y despejar el módulo del campo eléctrico

${\displaystyle E4\pi r^2=\frac{q}{{\epsilon }_0}}$

Se obtiene

${\displaystyle E=\frac{Qr}{4\pi {\epsilon }_0{R}^3}\text{( }r<R)E=\frac{Q}{4\pi {\epsilon }_0{r}^2}\text{( }r>R)}$

El campo en el exterior de una esfera cargada con carga Q, tiene la misma expresión que el campo producido por una carga puntual Q situada en su centro.

Potencial a una distancia r del centro de la esfera cargada

Se denomina potencial en un punto P a una distancia r del centro de la esfera cargada V(r) a la diferencia de potencial existente entre el punto P y el infinito V(r)-V(∞ ). Por convenio, se establece que en el infinito la energía potencial es cero.

Representamos el módulo del campo eléctrico E, en función de la distancia r al centro de la esfera cargada, en los intervalos 0< r<R y r>R

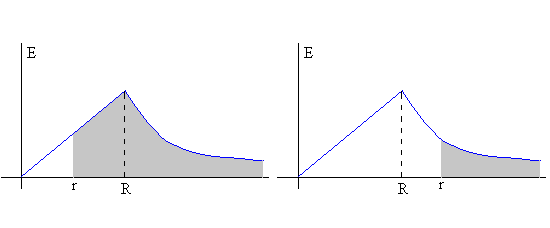
• r>R. Para hallar el potencial en un punto P que está fuera de la esfera cargada basta hallar el área sombreada (figura de la derecha)

${\displaystyle V={\displaystyle \underset{r}{\overset{\infty }{\int }}\frac{Q}{4\pi {\epsilon }_0{r}^2}dr=}\frac{Q}{4\pi {\epsilon }_{0}r}}$

• r<R. Para calcular el potencial en un punto P, en el interior de la esfera cargada, es necesario sumar dos áreas, por ser la función que describe la dependencia del campo E con r, discontinua en el punto r=R. (figura de la izquierda)

${\displaystyle V(r)={\displaystyle \underset{r}{\overset{R}{\int }}\frac{Qr}{4\pi {\epsilon }_0{R}^3}dr+}{\displaystyle \underset{R}{\overset{\infty }{\int }}\frac{Q}{4\pi {\epsilon }_0{r}^2}dr=}\frac{Q}{4\pi {\epsilon }_{0}r}=\frac{Q}{4\pi {\epsilon }_{0}R}\left(\frac{3}{2}-\frac{1}{2}\frac{r^2}{R^2}\right)}$

Energía de ionización

La energía de ionización, es la energía mínima necesaria para sacar al electrón situado en el origen de la esfera cargada hasta el infinito.

${\displaystyle W_1=qV(0)=\frac{3}{2}\frac{qQ}{4\pi {\epsilon }_{0}R}}$

Para un átomo con un electrón q=Q=e=1.6 10^-19 C. R≈ 10^-10 m. W₁=3.456 10^-18 J=21.6 eV.

Que es algo mayor que la energía de ionización del electrón en un átomo de hidrógeno en el estado fundamental, 13.6 eV.

Energía potencial de una distribución de cargas

Vamos a calcular ahora la energía necesaria para formar la distribución uniforme de carga positiva. O bien, la energía que se liberaría cuando la distribución uniforme de carga positiva explotase de modo que cada parte de ella estuviese a una distancia infinita una de la otra.

Determinaremos la expresión de la energía de un sistema de tres cargas, y la generalizamos para una distribución continua de carga.

Consideremos un sistema de tres cargas puntuales fijas q₁, q₂ y q₃, tal como se indica en la figura.

La energía de este sistema U vale

${\displaystyle U=E_{p12}+E_{p13}+E_{p23}=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{r_{12}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_3}{r_{13}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_2{q}_3}{r_{23}}}$

Llamando V₁ al potencial producido por las cargas q₂ y q₃ en la posición que ocupa q₁. La energía de la carga q₁ en el campo producido por las otras dos es

${\displaystyle q_1{V}_1=q_1\left(\frac{1}{4\pi {\epsilon }_0}\frac{q_3}{r_{13}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_2}{r_{12}}\right)=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_3}{r_{13}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{r_{12}}}$

Análogamente, llamando V₂ al potencial producido por las cargas q₁ y q₃ en la posición que ocupa q₂. La energía de la carga q₂ en el campo producido por las otras dos es

${\displaystyle q_2{V}_2=q_2\left(\frac{1}{4\pi {\epsilon }_0}\frac{q_1}{r_{12}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_3}{r_{23}}\right)=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{r_{12}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_2{q}_3}{r_{23}}}$

Del mismo modo, llamando V₃ al potencial producido por las cargas q₁ y q₂ en la posición que ocupa q₃. La energía de la carga q₃ en el campo producido por las otras dos es

${\displaystyle q_3{V}_3=q_3\left(\frac{1}{4\pi {\epsilon }_0}\frac{q_1}{r_{13}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_2}{r_{23}}\right)=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_3}{r_{13}}+\frac{1}{4\pi {\epsilon }_0}\frac{q_2{q}_3}{r_{23}}}$

Sumando estas tres contribuciones obtenemos el doble de la energía del sistema de partículas

${\displaystyle U=\frac{1}{2}\left(q_1{V}_1+q_2{V}_2+q_3{V}_3\right)=\frac{1}{2}{\displaystyle \sum q_i{V}_i}}$

Energía de la esfera cargada

Volviendo de nuevo a la esfera uniformemente cargada, el potencial V_i se sustituye por el potencial en la posición r, V(r) que hemos calculado previamente.

La carga q_i se sustituye por la carga que hay en la capa esférica comprendida entre r y r+dr. El volumen de dicha capa esférica es 4π r²dr, y la carga que hay en este volumen vale (densidad de carga por volumen)

${\displaystyle \frac{3Q{r}^2}{R^3}dr}$

La energía vale entonces

${\displaystyle W_2=\frac{1}{2}{\displaystyle \underset{0}{\overset{R}{\int }}V(r)dq}=\frac{1}{2}{\displaystyle \underset{0}{\overset{R}{\int }}\frac{Q}{4\pi {\epsilon }_{0}R}\left(\frac{3}{2}-\frac{1}{2}\frac{r^2}{R^2}\right)\frac{3Q{r}^2}{R^3}dr}=\frac{3}{5}\frac{Q^2}{4\pi {\epsilon }_{0}R}}$

Energía total del átomo de Kelvin-Thomson

La energía total de nuestro modelo de átomo de hidrógeno Q=q=e, es la diferencia entre dos energías:

• la energía necesaria para formar la distribución uniforme de carga positiva W₂
• la energía necesaria para sacar el electrón de la atracción de dicha carga W₁ (energía de ionización)

${\displaystyle W=W_2-W_1=-\frac{9}{10}\frac{e^2}{4\pi {\epsilon }_{0}R}}$

Curso Interactivo de Física en Internet © Ángel Franco García