Movimiento del electrón en el átomo de Kelvin-Thomson

Supongamos que el electrón se puede mover libremente en el interior de la distribución esférica de carga positiva. En un instante dado, se encuentra a una distancia x del centro de dicha distribución.

Aplicando la ley de Gauss (r<R) hemos obtenido la expresión del campo eléctrico creado por la distribución de carga positiva a la distancia r=x del centro. Dicho campo tiene dirección radial y sentido hacia afuera.

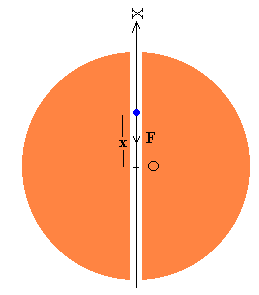thomson4.gif (2687 bytes) La fuerza sobre electrón es el producto de la carga por el campo. Tiene dirección radial y sentido (atractivo) hacia el centro de la distribución de carga positiva.

$F = - q E = - \frac{1}{4 π ε_{0}} \frac{Q q x}{R^{3}}$

Como vemos la fuerza es proporcional al desplazamiento x y de sentido contrario a este. Una clara indicación de que el electrón describirá un M.A.S.

$\frac{d^{2} x}{d t^{2}} + \frac{1}{4 π ε_{0}} \frac{Q q}{m R^{3}} x = 0$

cuya frecuencia angular vale

$ω^{2} = \frac{1}{4 π ε_{0}} \frac{Q q}{m R^{3}}$

Para un átomo con un electrón q=Q=e=1.6 10^-19 C. R≈ 10^-10 m, y m=9.1 10^-31 kg, se obtiene f =2πω =2.53 10¹⁵ Hz.

Cuando un electrón pasa del primer estado excitado al estado fundamental, emite radiación de frecuencia 2.47 10¹⁵ Hz que es del orden de la frecuencia f de su Movimiento Armónico Simple.

Un problema completamente análogo es el movimiento de un cuerpo a lo largo de un túnel excavado en la Tierra, supuesta una distribución esférica y uniforme de masa.

Actividades.

En este applet se muestra como un electrón (círculo de color azul) describe un M.A.S. en el interior de una distribución esférica y uniforme de carga positiva.

Se introduce

la carga del átomo o ión hidrogenoide Q (en unidades de la carga del electrón), en el control de selección titulado Carga
el radio del átomo o ión hidrogenoide R (en angstroms), en el control de selección titulado Radio

Se pulsa en el botón titulado Empieza.

Ejemplo: El cuadrado de la frecuencia angular ω es

$ω^{2} = 9 \cdot 10^{9} \frac{Q \cdot 1.6 \cdot 10^{- 19} \cdot 1.6 \cdot 10^{- 19}}{9.1 \cdot 10^{- 31} {(R \cdot 10^{- 10})}^{3}} = 2.531 \cdot 10^{32} \frac{Q}{R^{3}}$

Para Q=1 y R=1 el periodo es P=2π/ω=3.94·10^-16 s y la frecuencia f=1/P=2.53·10¹⁵ Hz
Para Q=4 y R=0.5 el periodo es P=0.07·10^-15 s y la frecuencia f=14.3·10¹⁵ Hz

A la derecha del applet, se representa su posición en función del tiempo. A partir de las medidas efectuadas en la gráfica podemos determinar aproximadamente su periodo. El tiempo obtenido hay que multiplicarlo por el factor 10^-15 s.

Las ecuaciones de su movimiento son

x=x₀sin(ω t+φ)
v=ω x₀cos(ω t+φ)

Como el electrón se suelta en la posición inicial x₀ con velocidad nula v=0, la ecuación de su MAS es x=x₀cos(ω t). La posición inicial del electrón se ha tomado arbitrariamente igual a las tres cuartas partes del radio del átomo x₀=3R/4.

LineasApplet aparecerá en un explorador compatible JDK 1.1