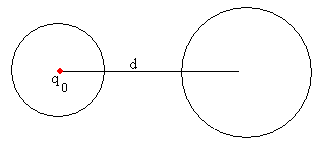El método de las imágenes

Dos esferas conductoras una de las cuales está a potencial cero

Consideremos el caso de dos esferas de radios r y R cuyos centros están separados una distancia d>r+R. La primera esfera está a una potencial V y la segunda esfera está conectada a Tierra, V=0

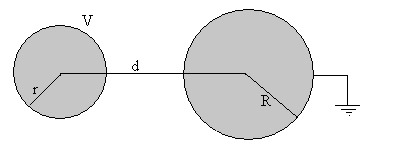
Sustituiremos las dos esferas por dos sucesiones de cargas puntuales que convergen rápidamente a cero, y que hacen que las dos superficies esféricas sean equipotenciales.

Los pasos para aplicar el método de las imágenes son los siguientes:

Colocamos en el centro de la primera esfera de radio r una carga q₀, de modo que el potencial de la esfera sea V.

$V = \frac{1}{4 π ε_{0}} \frac{q_{0}}{r}$

La superficie esférica de radio R deja de ser equipotencial, por lo que ponemos una carga Q₁ en el interior de la segunda esfera a una distancia X₁ de su centro

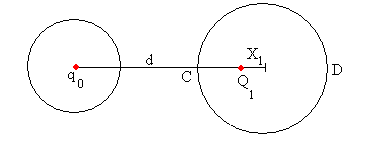
Calculamos el valor de Q₁ y su posición X₁ para que la segunda esfera de radio R sea una superficie equipotencial, aunque deje de serlo la primera esfera de radio r.

El potencial en C (d-R, 0) debido a las cargas q₀ y Q₁ lo hacemos cero

$\frac{q_{0}}{d - R} + \frac{Q_{1}}{R - X_{1}} = 0$

El potencial en D (d+R, 0) debido a las cargas q₀ y Q₁ lo hacemos cero

$\frac{q_{0}}{d + R} + \frac{Q_{1}}{R + X_{1}} = 0$

Despejamos Q₁ y X₁ de este sistema de dos ecuaciones con dos incógnitas

$X_{1} = \frac{R^{2}}{d} Q_{1} = - q_{0} \frac{R}{d}$

La superficie esférica de radio r deja de ser equipotencial, por lo que ponemos una carga q₁ en el interior de primera esfera a una distancia x₁ de su centro

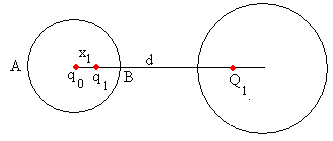
Calculamos el valor de q₁ y su posición x₁ para que la primera esfera de radio r sea una superficie equipotencial, aunque deje de serlo la segunda esfera de radio R.

El potencial en A (-r, 0) debido a las cargas q₁ y Q₁ lo hacemos cero

$\frac{q_{1}}{r + x_{1}} + \frac{Q_{1}}{d + r - X_{1}} = 0$

El potencial en B (r, 0) debido a las cargas q₁ y Q₁ lo hacemos cero

$\frac{q_{1}}{r - x_{1}} + \frac{Q_{1}}{d - r - X_{1}} = 0$

Despejamos q₁ y x₁ en este sistema de dos ecuaciones con dos incógnitas

$x_{1} = \frac{r^{2}}{d - X_{1}} q_{1} = - Q_{1} \frac{r}{d - X_{1}} = q_{0} \frac{r R}{d^{2} - R^{2}}$

La superficie esférica de radio R deja de ser equipotencial, por lo que ponemos una carga Q₂ en el interior de la segunda esfera a una distancia X₂ de su centro

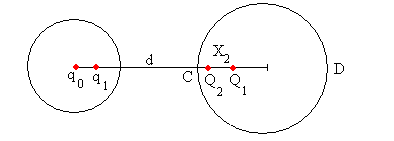
Calculamos el valor de Q₂ y su posición X₂ para que la segunda esfera de radio R sea una superficie equipotencial, aunque deje de serlo la primera esfera de radio r.

El potencial en C (d-r, 0) debido a las cargas Q₂ y q₁ lo hacemos cer

$\frac{Q_{2}}{R - X_{2}} + \frac{q_{1}}{d - R - x_{1}} = 0$

El potencial en D (d+r, 0) debido a las cargas Q₂ y q₁ lo hacemos cero

$\frac{Q_{2}}{R + X_{2}} + \frac{q_{1}}{d + R - x_{1}} = 0$

Despejamos Q₂ y X₂ en este sistema de dos ecuaciones con dos incógnitas

$X_{2} = \frac{R^{2}}{d - x_{1}} Q_{2} = - q_{1} \frac{R}{d - x_{1}} = - q_{0} \frac{r R^{2}}{d^{3} - d R^{2} - d r^{2}}$

La superficie esférica de radio r deja de ser equipotencial, por lo que ponemos una carga q₂ en el interior de primera esfera a una distancia x₂ de su centro

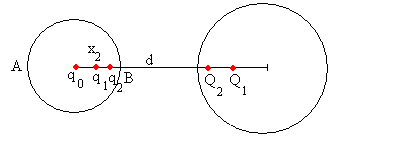
Calculamos el valor de q₂ y su posición x₂ para que la primera esfera de radio r sea una superficie equipotencial, aunque deje de serlo la segunda esfera de radio R.

El potencial en A (-r, 0) debido a las cargas q₂ y Q₂ lo hacemos cero

$\frac{q_{2}}{r + x_{2}} + \frac{Q_{2}}{d + r - X_{2}} = 0$

El potencial en B (r, 0) debido a las cargas q₂ y Q₂ lo hacemos cero

$\frac{q_{2}}{r - x_{2}} + \frac{Q_{2}}{d - r - X_{2}} = 0$

Despejamos q₂ y x₂ en este sistema de dos ecuaciones con dos incógnitas

$x_{2} = \frac{r^{2}}{d - X_{2}} q_{2} = - Q_{2} \frac{r}{d - X_{2}} = - q_{0} \frac{r^{2} R^{2}}{d^{4} - 2 R^{2} d^{2} - r^{2} d^{2} + R^{4}}$

y así, sucesivamente

Relaciones recursivas

Podemos calcular la sucesión de cargas q_i, Q_i y sus posiciones x_i, X_i mediante las relaciones recursivas

$\begin{array}{l} X_{i + 1} = \frac{R^{2}}{d - x_{i}} Q_{i + 1} = - q_{i} \frac{R}{d - x_{i}} i = 0, 1, 2 ... \\ x_{i + 1} = \frac{r^{2}}{d - X_{i + 1}} q_{i + 1} = - Q_{i + 1} \frac{r}{d - X_{i + 1}} \\ x_{0} = 0 X_{0} = 0 Q_{0} = 0 \end{array}$

Ejemplo:

Sea d=5, r=1, R=0.5, V₁=1, V₂=0

Ponemos una carga q₀ en el centro de la primera esfera

V₁=q₀/r, q₀=1

Paso	Posición x_i	Carga q_i	Posición X_i	Carga Q_i
0	0	1	0	0
1	0.20202	0.020202	0.05	-0.1
2	0.20211	0.000425	0.05211	-0.002105
3	0.20211	0.000009	0.05211	-0.000044

Campo y potencial producido por la sucesión de cargas

Calculamos el campo y el potencial producido en el punto P (x, y) por el par de cargas q_i situada en el punto x_i y Q_i en la posición d-X_i

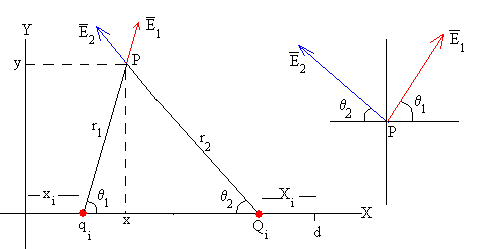
El campo E₁ producido por la carga q_i es

$E_{1} = \frac{1}{4 π ε_{0}} \frac{q_{i}}{{(x - x_{i})}^{2} + y^{2}}$

El campo E₂ producido por la carga Q_i es

$E_{2} = \frac{1}{4 π ε_{0}} \frac{Q_{i}}{{(d - x - X_{i})}^{2} + y^{2}}$

Las componentes del campo total E_i son

E_ix=E₁·cosθ₁-E₂·cosθ₂
E_iy=E₁·sinθ₁+E₂·sinθ₂

$\begin{array}{l} E_{i x} = \frac{q_{i}}{4 π ε_{0}} \frac{x - x_{i}}{{({(x - x_{i})}^{2} + y^{2})}^{3 / 2}} - \frac{Q_{i}}{4 π ε_{0}} \frac{d - x - X_{i}}{{({(d - x - X_{i})}^{2} + y^{2})}^{3 / 2}} \\ E_{i y} = \frac{q_{i}}{4 π ε_{0}} \frac{y}{{({(x - x_{i})}^{2} + y^{2})}^{3 / 2}} + \frac{Q_{i}}{4 π ε_{0}} \frac{y}{{({(d - x - X_{i})}^{2} + y^{2})}^{3 / 2}} \end{array}$

El potencial V_i en el punto P debido a las dos cargas es

$V_{i} = \frac{1}{4 π ε_{0}} \frac{q_{i}}{\sqrt{{(x - x_{i})}^{2} + y^{2}}} + \frac{1}{4 π ε_{0}} \frac{Q_{i}}{\sqrt{{(d - x - X_{i})}^{2} + y^{2}}}$

El campo y el potencial total es la suma de todos los campos y potenciales producidos por los pares de cargas dispuestas simétricamente al plano

$E = \sum_{0}^{\infty} E_{i} V = \sum_{0}^{\infty} V_{i}$

Actividades

Se introduce

La distancia d entre los centros de ambas esferas, en unidades del radio a de la esfera, actuando en la barra de desplazamiento titulada Distancia
El radio de la segunda esfera R, en el control de edición titulado Radio 2
El potencial V₁ de la primera esfera, en el control de edición titulado Potencial 1
El potencial de la segunda esfera se ha fijado en V₂=0
El radio de la primera esfera se ha fijado en r=1

Se pulsa el botón titulado Nuevo

Si la distancia d entre los centros de las dos esferas es menor que r+R+0.5, el programa no prosigue e invita al usuario a modificar los datos de entrada

Se trazan las líneas de fuerza (en color blanco) y las superficies equipotenciales (en color azul claro).

LineasApplet aparecerá en un explorador compatible JDK 1.1