Campo magnético producido por un toroide
Aplicamos la ley de Ampère para determinar el campo producido por un toroide de radio medio R.
Si tomamos un solenoide, lo curvamos y pegamos sus extremos obtenemos un anillo o toroide.
- Las líneas de campo magnético que en el solenoide son segmentos rectos se transforman en circunferencias concéntricas en el solenoide. El campo magnético es tangente en cada punto a dichas circunferencias. El sentido de dicho campo viene determinado por la regla de la mano derecha.
- Elegimos como camino cerrado una circunferencia de radio r, cuyo centro está en el eje del toroide, y situada en su plano meridiano.
- El campo magnético B es tangente a la circunferencia de radio r.
- El campo magnético B tiene el mismo módulo en todos los puntos de dicha circunferencia.
La circulación (el primer miembro de la ley de Ampère) vale
- Vamos a calcular ahora la intensidad que atraviesa la circunferencia de radio r (en color azul) en los tres casos siguientes.
- Fuera del toroide (r<R)
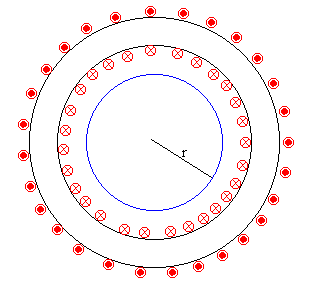 |
Como vemos en la figura, la intensidad que atraviesa la circunferencia de
radio r (en color azul) es cero. Aplicando la ley de Ampère
B·2π r=μ0 0 B=0 |
- Dentro del toroide
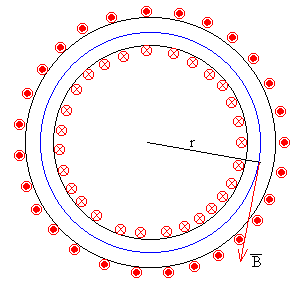 |
Cada espira del toroide atraviesa una vez el camino cerrado (la
circunferencia de color azul de la figura) la intensidad será Ni, siendo N el número de espiras e i la intensidad que circula por cada
espira.
|
- Fuera del toroide (r>R)
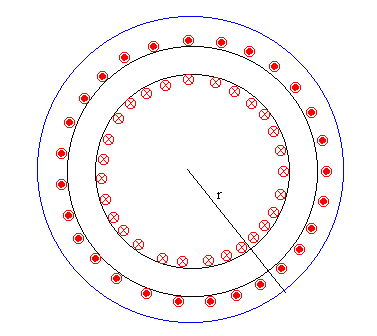 |
Cada espira del toroide atraviesa dos veces el camino cerrado
(circunferencia de color azul de la figura) transportando intensidades de sentidos
opuestos .
La intensidad neta es Ni-Ni=0, y B=0 en todos los puntos del camino cerrado. |
El campo magnético está completamente confinado en el interior del toroide.