• Inicio
• Electromagnetismo
• Campo eléctrico
• Condensadores

Condensador cilíndrico

El campo existente entre las armaduras de un condensador cilíndrico de radio interior a, radio exterior b, y longitud L, cargado con cargas +Q y –Q, respectivamente, se calcula aplicando la ley de Gauss a la región a<r<b, ya que tanto fuera como dentro del condensador el campo eléctrico es cero.

La aplicación del teorema de Gauss, es similar al de una línea cargada,y  requiere los siguientes pasos:

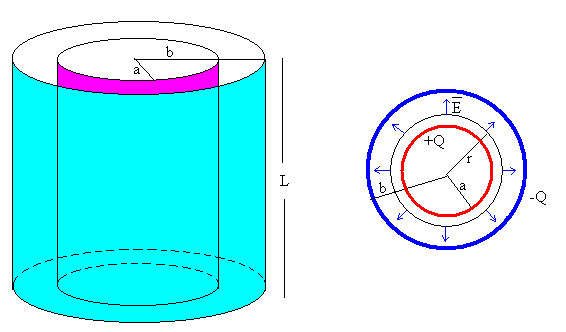
1.-A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.

La dirección del campo es radial y perpendicular al eje del cilindro.

2.-Elegir una superficie cerrada apropiada para calcular el flujo

Tomamos como superficie cerrada, un cilindro de radio r, y longitud L. Tal como se muestra en la figura. El cálculo del flujo, tiene dos componentes

• Flujo a través de las bases del cilindro: el campo y el vector superficie son perpendiculares, el flujo es cero.

• Flujo a través de la superficie lateral del cilindro. El campo E es paralelo al vector superficie dS, y el campo es constante en todos los puntos de la superficie lateral, por lo que,

${\displaystyle {\displaystyle \underset{S}{\int }E\cdot dS}={\displaystyle \underset{S}{\int }EdS\cos 0º}=E{\displaystyle \underset{S}{\int }dS}=E2\pi rL}$

El flujo total es por tanto; E·2π rL

3. Determinar la carga que hay en el interior de la superficie cerrada

La carga en el interior de la superficie cerrada vale +Q, que es la carga de la armadura cilíndrica interior

4.-Aplicar el teorema de Gauss y despejar el módulo del campo eléctrico

${\displaystyle E2\pi rL=\frac{Q}{{\epsilon }_0}E=\frac{Q}{2\pi {\epsilon }_{0}rL}}$

Ahora, es fácil demostrar, aplicando el teorema de Gauss que el campo en las regiones r<a y r>b es nulo.

• En el primer caso, si tomamos una superficie cilíndrica de radio r<a y de longitud L, dicha superficie no encierra carga alguna.
• En el segundo caso, si tomamos una superficie cilíndrica de radio r>b y longitud L, la carga total encerrada es +Q-Q=0, es nula, el flujo es cero y el campo es cero.

En la figura, se muestra la representación gráfica del campo E en función de la distancia radial r.

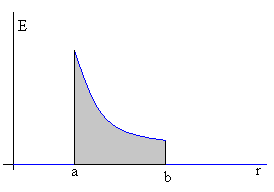La diferencia de potencial entre las placas del condensador se calcula integrando, (área sombreada de la figura).

${\displaystyle V-V\text{'}={\displaystyle \underset{a}{\overset{b}{\int }}E\cdot dr}=\frac{Q}{2\pi {\epsilon }_{0}L}\ln \frac{b}{a}}$

La capacidad es

${\displaystyle C=\frac{Q}{V-V\text{'}}=\frac{2\pi {\epsilon }_{0}L}{\ln (b/a)}}$

La capacidad solamente depende de la geometría del condensador (radio a y radio b de sus armaduras, y longitud L del condensador)

Si el cilindro interior no está completamente introducido en el exterior, sino solamente una longitud x, la capacidad del condensador será

${\displaystyle C=\frac{2\pi {\epsilon }_{0}x}{\ln (b/a)}}$

Energía del condensador

${\displaystyle U=\frac{1}{2}C{V}^2}$

Electrómetro cilíndrico

La fuerza que actúa sobre el cilindro interior del condensador, manteniendo constante el potencial V entre sus placas es

${\displaystyle F={\left(\frac{\partial W}{\partial x}\right)}_V=\frac{2\pi {\epsilon }_0}{\ln (b/a)}{V}^2}$

La fuerza es constante e independiente de x.

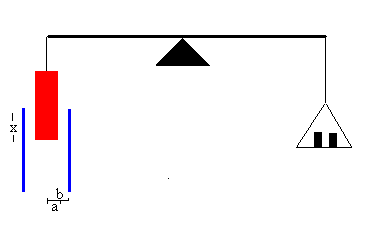
Actividades

En el applet se trata de medir una tensión desconocida V, mediante un electrómetro formado por dos armaduras cilíndricas de radios a y b que tienen el mismo eje.

El potencial V se calcula midiendo la fuerza F, conocidos los datos del radio interior a y el radio exterior b del condensador cilíndrico.

Cuando se pulsa el botón titulado Nuevo, se genera un número aleatorio que representa la tensión V desconocida de un generador.

Cuando se pulsa el botón titulado Conectar, las placas del condensador se conectan a dicho generador. El cilindro interior es atraído por el campo eléctrico y la balanza se desequilibra. Tenemos que volverla a equilibrar para medir la fuerza de atracción F.

Moviendo los cursores (flechas de color azul, rojo y negro) equilibramos la balanza y medimos la fuerza en miligramos.

Ejemplo:

Equilibramos la balanza desplazando con el puntero del ratón los cursores hasta marcar 57.7 mg.

Sabiendo que el radio interior a del cilindro es de 45 mm, y el radio del cilindro exterior es de 50 mm. Introducimos los datos en la fórmula de la fuerza en las unidades adecuadas.

${\displaystyle 57.7\cdot {10}^{-6}\cdot 9.8=\frac{\pi \cdot V^2}{4\pi 9\cdot {10}^9\cdot \ln \frac{50}{45}}V=1464.5}$

Comparamos nuestros cálculos con la respuesta dada por el programa interactivo 1465.5 V, al pulsar el botón titulado Respuesta.

LineasApplet aparecerá en un explorador compatible JDK 1.1

Curso Interactivo de Física en Internet © Ángel Franco García