Movimiento en campos eléctrico y magnético cruzados (II)

Dos partículas de la misma masa m cargadas con cargas iguales y opuestas q, están situadas a ambos lados del origen, en el eje X, en las posiciones ±x₀, respectivamente.

Las partículas se mantienen en reposo en un campo magnético uniforme B perpendicular a la línea que conecta las cargas. Las partículas se liberan simultáneamente. Vamos a estudiar su movimiento posterior bajo la fuerza de atracción mutua y bajo la fuerza que ejerce el campo magnético.

Descripción

Estudiamos el movimiento de la carga positiva, el movimiento de la carga negativa será simétrico.

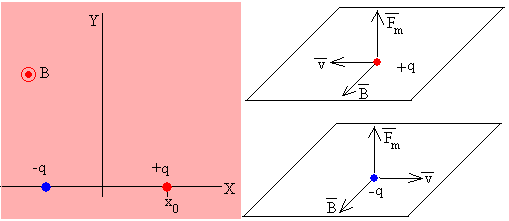
La fuerza de atracción eléctrica que ejerce la carga negativa sobre la carga positiva es

$F_{e} = - \frac{1}{4 π ε_{0}} \frac{q^{2}}{{(2 x)}^{2}} \hat{i}$

La fuerza que ejerce el campo magnético sobre la carga positiva es

$F_{m} = q v \times B = q (v_{x} \hat{i} + v_{y} \hat{j}) \times B \hat{k} = q B v_{y} \hat{i} - q B v_{x} \hat{j}$

La ecuación del movimiento es

$m \frac{d^{2} r}{d t^{2}} = F_{e} + F_{m}$

o bien,

$\begin{array}{l} m \frac{d^{2} x}{d t^{2}} = - \frac{1}{4 π ε_{0}} \frac{q^{2}}{4 x^{2}} + q B v_{y} \\ m \frac{d v_{y}}{d t} = - q v_{x} B \end{array}$

La segunda ecuación se puede integrar

$\begin{array}{l} m \frac{d v_{y}}{d t} = - q B \frac{d x}{d t} \\ v_{y} = - \frac{q B}{m} x + c \end{array}$

La constante de integración c, se calcula a partir de las condiciones iniciales: en la posición inicial x₀, la velocidad inicial v_y=0

$v_{y} = \frac{q B}{m} (x_{0} - x)$

Nos queda por resolver el sistema formado por una ecuación diferencial de segundo orden y una ecuación diferencial de primer orden

$\begin{array}{l} \frac{d^{2} x}{d t^{2}} = - \frac{1}{4 π ε_{0}} \frac{q^{2}}{4 m} \frac{1}{x^{2}} + \frac{q^{2} B^{2}}{m^{2}} (x_{0} - x) \\ \frac{d y}{d t} = \frac{q B}{m} (x_{0} - x) \end{array}$

con las condiciones iniciales siguientes: en el instante t=0, x=x₀, y=0, v_x=0.

Se resuelve por el procedimiento numérico de Runge-Kutta.

Campo magnético crítico

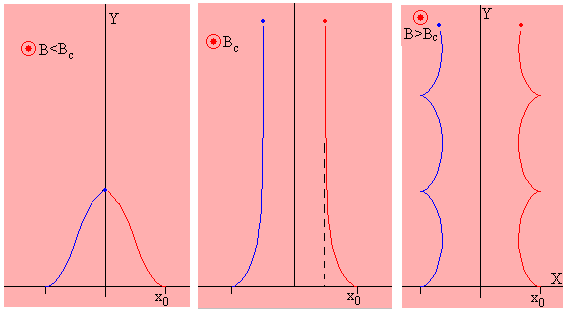
Como podemos ver en las figuras, en unos casos las partículas chocan en un punto del eje Y (figura de la izquierda) y en otros, la partícula describe una trayectoria cíclica en la que se acerca al eje Y y regresa a la misma abscisa de partida x₀ (figura de la derecha). Existirá un caso crítico en el que la carga se mueve paralelamente al eje Y, es decir x=cte, v_x=0 (figura de en medio). En este caso

La fuerza de atracción eléctrica se compensa con la fuerza magnética

$\begin{array}{l} \frac{1}{4 π ε_{0}} \frac{q^{2}}{{(2 x)}^{2}} = q v_{y} B \\ \frac{1}{4 π ε_{0}} \frac{q^{2}}{{(2 x)}^{2}} = \frac{q^{2} B^{2}}{m} (x_{0} - x) \\ x^{2} (x_{0} - x) = \frac{1}{4 π ε_{0}} \frac{m}{4 B^{2}} \end{array}$

Como la fuerza magnética no realiza trabajo alguno, el trabajo de la fuerza eléctrica es igual a la variación de energía cinética

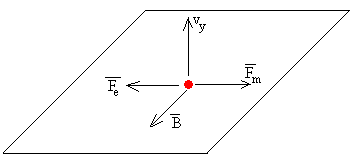
$\begin{array}{l} \int_{A}^{B} F_{e} \cdot d r = \int_{x_{0}}^{x} - \frac{1}{4 π ε_{0}} \frac{q^{2}}{4 x^{2}} d x = \frac{1}{2} m v^{2} \\ v^{2} = \frac{1}{4 π ε_{0}} \frac{q^{2}}{2 m} (\frac{1}{x} - \frac{1}{x_{0}}) \end{array}$

Esta ecuación nos indica que la abscisa de la partícula x≤x₀, ya que v² es positivo

Cuando la partícula se mueve paralelamente al eje Y, v_x=0

$\begin{array}{l} v_{y}^{2} = \frac{1}{4 π ε_{0}} \frac{q^{2}}{2 m} (\frac{1}{x} - \frac{1}{x_{0}}) \\ \frac{q^{2} B^{2}}{m^{2}} {(x - x_{0})}^{2} = \frac{1}{4 π ε_{0}} \frac{q^{2}}{2 m} (\frac{1}{x} - \frac{1}{x_{0}}) \\ (x - x_{0}) x x_{0} = \frac{1}{4 π ε_{0}} \frac{m}{2 B^{2}} \end{array}$

De las ecuaciones de equilibrio y del trabajo-energía obtenemos x y x₀.

$x = \frac{x_{0}}{2} x_{0}^{3} = \frac{1}{4 π ε_{0}} \frac{2 m}{B^{2}}$

Ejemplo.

Colocamos un protón y un antiprotón en el eje X en las posiciones simétricas x₀=±1.0 mm. Calculamos el campo magnético crítico B_c que hace que las partículas se muevan paralelamente al eje Y.

Datos: masa del protón m=1.6725·10^-27 kg, carga q=1.6·10^-19 C

$B^{2} = \frac{1}{4 π ε_{0}} \frac{2 m}{x_{0}^{3}} B_{c} = \sqrt{\frac{2 \cdot 9 \cdot 10^{9} \cdot 1.6725 \cdot 10^{- 27}}{{(1.0 \cdot 10^{- 3})}^{3}}} = 1.7351 \cdot 10^{- 4} T = 1.7351 gauss$

La carga positiva se mueve al cabo de cierto tiempo paralelamente al eje Y a una distancia x=0.5 mm con una velocidad

$v_{y} = \frac{q B}{m} \frac{x_{0}}{2} v_{y} = \frac{1.6 \cdot 10^{- 19} \cdot 1.7351 \cdot 10^{- 4}}{2 \cdot 1.6725 \cdot 10^{- 27}} 1.0 \cdot 10^{- 3} = 8.3 m/s$

Actividades

Se introduce

La posición inicial de la carga positiva x₀, actuando en la barra de desplazamiento titulada Posición
El valor del campo magnético B, perpendicular el plano del applet y dirigido hacia el lector, actuando en la barra de desplazamiento titulada Campo

Se pulsa el botón titulado Empieza

Se dibuja la trayectoria de las partículas cargadas, se proporcionan los datos del tiempo t en ms, de la posición (x,y) en mm y de la velocidad (v_x, v_y) en m/s

ThomsonApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Physics Challenge for teachers and students. Solution to April 2007 challenge. The Physics Teacher, Vol 45, 2007.