Calor latente de fusión

Medida del calor latente de fusión

Se introduce una masa m de hielo a un calorímetro con agua a una temperatura T ligeramente por encima de la temperatura ambiente T_a y se agita la mezcla hasta que el hielo se funde completamente. Se elige la masa m del hielo de modo que la temperatura T_e de equilibrio esté ligeramente por debajo de la temperatura ambiente, es decir, de modo que T-T_a≈T-T_e.De este modo, el calor cedido al ambiente en la primera etapa de la experiencia se compensa con el calor ganado en la segunda etapa.

En la experiencia que se describe a continuación, se emplea el procedimiento de las mezclas pero no se tiene en cuenta las pérdidas o ganancias de calor entre el calorímetro y el medio ambiente.

Una masa m_a de agua a la temperatura inicial T_a se mezcla con una masa m_h de hielo a 0º C en un calorímetro. La mezcla de agua y hielo se agita hasta que se alcanza una temperatura final de equilibrio T_e.

Pueden ocurrir dos casos

Se funde una parte m de la masa inicial m_h de hielo, quedando una mezcla formada por hielo (m_h-m) y agua (m_a+m) a la temperatura final de T_e=0ºC.

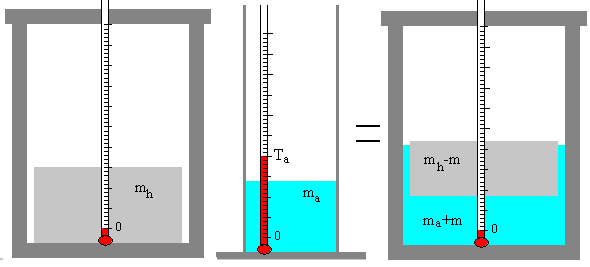
El calor absorbido por el hielo es Q₁=m·L_f
El calor cedido por el agua es Q₂=m_a·c·(0-T_a)

Si el calorímetro está perfectamente aislado, no pierde ni gana calor, se cumplirá que

$\begin{array}{l} Q_{1} + Q_{2} = 0 \\ L_{f} = \frac{m_{a} c T_{a}}{m} \end{array}$ (1)

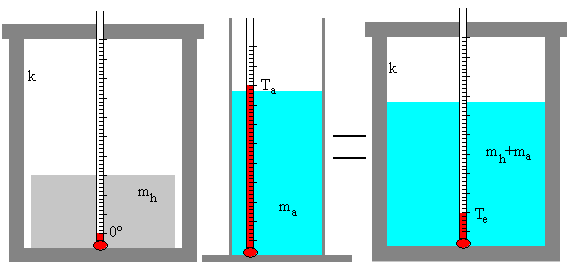
Si se funde todo el hielo, el estado final es una masa (m_h+m_a) de agua a la temperatura final T_e>0.

Ahora hemos que tener en cuenta que la masa m_h de hielo se convierte en agua y a continuación, eleva su temperatura de 0ºC a T_e. Por otra parte, el calorímetro (su masa equivalente en agua k) eleva su temperatura de 0º C a T_e.

El calor absorbido por el hielo es Q₁=m_h·L_f+ m_h·c·(T_e-0)
Calor absorbido por el calorímetro Q₂= k·c·(T_e-0)
El calor cedido por el agua es Q₃=m_a·c·(T_e-T_a)

Si el calorímetro está perfectamente aislado, no pierde ni gana calor, se cumplirá que

$\begin{array}{l} Q_{1} + Q_{2} + Q_{3} = 0 \\ L_{f} = c (T_{a} \frac{m_{a}}{m_{h}} - T_{e} \frac{m_{a} + m_{h} + k}{m_{h}}) \end{array}$ (2)

En la página “calor específico de un sólido”, ya se ha explicado el significado de masa equivalente k en agua del calorímetro.

Actividades

Medida del equivalente en agua del calorímetro

Introducimos los siguientes datos:

Masa M de agua en gramos en el calorímetro,
Temperatura T₀ inicial del calorímetro
Masa m de agua en gramos en una probeta
Temperatura T del agua

Se pulsa el botón titulado Preparar, los termómetros y las escalas graduadas de medida del volumen de agua reflejan los datos introducidos.

Si estamos conformes, se pulsa el botón titulado Calcular. La masa m de agua se vierte en el calorímetro y en el termómetro podemos leer la temperatura final de equilibrio T_e.

Ejemplo:

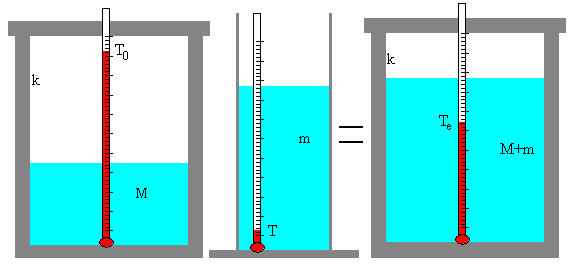
Sea M=170 g, T₀=92.7 ºC
Sea m=170 g, y T=2.7 ºC
La temperatura de equilibrio es T_e=54.2ºC

El equivalente en agua del calorímetro será

$k = \frac{m (T - T_{e})}{T_{e} - T_{0}} - M k = \frac{170 \cdot (2.7 - 54.2)}{54.2 - 92.7} - 170 = 57.4 g$

Medida del calor de fusión

Introducimos los siguientes datos:

Masa m_h de hielo en gramos en el calorímetro,
Temperatura inicial del hielo se fija en 0ºC

Masa m_a del agua en gramos
Temperatura T_a del agua

Se pulsa el botón titulado Preparar.

Si estamos conformes, se pulsa el botón titulado Calcular. El agua se vierte en el calorímetro y en el termómetro podemos leer la temperatura final de equilibrio T_e.

En el caso de que solamente una parte del hielo se fundiese, la temperatura final sería T_e=0ºC. Se podría extraer el hielo del calorímetro, y pesarlo en una balanza. Conocida la masa m de hielo se determinaría el calor de fusión mediante la fórmula (1). Cuando se produzca esta situación, se incrementa la masa de agua o su temperatura o ambas cosas a la vez, hasta conseguir que todo el hielo del calorímetro se funda.

Ejemplo:

Hielo: m_h=128 g,
Agua, m_a=170 g, y T_a=80ºC
Se funde todo el hielo y la temperatura final de equilibrio es T_e=9.5 ºC
La masa equivalente en agua del calorímetro la hemos calculada en el apartado anterior k=57.4 g

$L_{f} = 4180 (80 \frac{170}{128} - 9.5 \frac{170 + 128 + 57.4}{128}) = 333868 J/kg$

Referencias

Güemez, Fiolhais C., Fiolhais M. Revisiting Black's experiments on the latent heats of water. The Physics Teacher Vol 40, January 2002, pp. 26-31