Presión producida por la curvatura de una superficie

Young y Laplace dedujeron de forma independiente en 1805 la fórmula de la diferencia de presión entre el interior y el exterior de una superficie esférica de radio R.

La fórmula de Young-Laplace demuestra que la presión en el interior de de una superficie esférica es siempre mayor que en el exterior, que la diferencia de presión se incrementa cuando disminuye al radio de dicha superficie, y que se hace cero cuando la superficie es plana (radio infinito).

Los líquidos tienden a minimizar su superficie. Por esta razón, las gotas tienen forma esférica en ausencia de gravedad. La tensión superficial tiende a reducir el área de la superficie y por tanto, el volumen de la gota. La diferencia de presión tiende a incrementar el volumen de la gota, la condición de equilibrio se alcanza cuando ambas tendencias se compensan.

Presión producida por la curvatura de una superficie

Vamos a mostrar que en el interior de una gota o una burbuja en equilibrio hay una presión superior a la exterior. Este exceso de presión es debido a la curvatura de la superficie límite de separación.

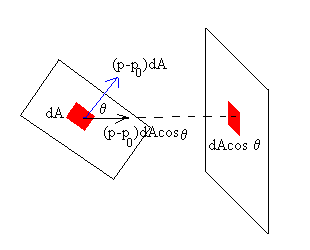Las fuerzas de presión ejercen una fuerza que es normal a la superficie.

Supongamos que la presión en el interior de la burbuja es p y en el exterior es p₀, entonces la fuerza sobre una porción dA de la lámina es (p-p₀)dA, su componente X es (p-p₀)dAcosθ . Pero dAcosθ es la proyección del área sobre un plano perpendicular al eje X.

La diferencia de presión entre el interior de la burbuja y el exterior origina fuerzas sobre la superficie de la burbuja perpendiculares a la superficie esférica, tal como indican las flechas azules de la figura de abajo. Su proyección a lo largo del eje horizontal X, será el producto de la diferencia de presión (p-p₀) por el área proyectada sobre un plano perpendicular al eje X (la proyección de una semiesfera de radio R, sobre un plano es un círculo de área π R².

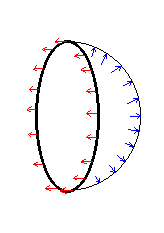tension_4.gif (2151 bytes) Una burbuja está formada por dos láminas superficiales esféricas muy próximas entre sí. Consideremos la mitad de la burbuja y busquemos las fuerzas que mantienen a esa porción en equilibrio.

La fuerza que origina la diferencia de presión es F₁= (p-p₀) π R²
Fuerza originada por la tensión superficial

La mitad izquierda de la burbuja (no representada) ejerce una fuerza hacia la izquierda igual a dos veces la tensión superficial por el perímetro (flechas rojas en la figura) F₂=2γ ·2π R

En el equilibrio F₁=F₂

$p - p_{0} = \frac{4 γ}{R}$

la diferencia de presiones es tanto mayor cuanto menor es el radio R. Esta expresión es un caso particular de la denominada ley de Laplace.

El factor cuatro aparece por que una pompa de jabón tiene dos caras: interior y exterior. En el caso de una gota de agua, solamente hay una cara por lo que la diferencia de presión se reduce a la mitad.

Deducción alternativa de la ecuación de Laplace para una gota

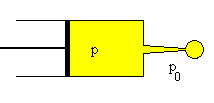laplace1.gif (1457 bytes) Supongamos una gota que se forma en el extremo de una jeringa al desplazar el émbolo, tal como se indica en la figura.

Sea p₀ la presión exterior. Para formar la gota de radio r es necesario aplicar mediante el émbolo una presión p algo mayor que p₀.

El trabajo realizado por el émbolo sobre el líquido al desplazarse es p·dV . Pero la gota realiza un trabajo p₀·dV sobre su entorno ya que desplaza el aire al incrementar su volumen dV. Ambos volúmenes son iguales debido a que el líquido es incomprensible.

El trabajo total sobre el líquido será dW=(p-p₀)·dV

Este trabajo se emplea en incrementar la superficie de la gota, mientras se mantiene la temperatura y el volumen del líquido constantes. dW=γ dA

Igualando ambos trabajos y teniendo en cuenta las fórmulas del área y del volumen de una superficie esférica.

$\begin{array}{l} V = \frac{4}{3} π r^{3} A = 4 π r^{2} \\ d V = 4 π r^{2} \cdot d r d A = 8 π r \cdot d r \\ p - p_{0} = \frac{2 γ}{R} \end{array}$

Comunicando dos pompas de jabón

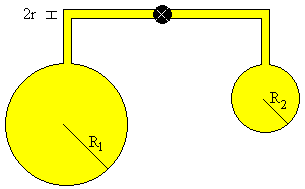Si ponemos dos pompas de jabón de radios R₁ y R₂ en los extremos de un tubo, y abrimos la llave que las comunica veremos que la pompa de jabón de radio menor es "comida" por la pompa de radio mayor.

La diferencia de presión entre el exterior y el interior de una pompa de jabón es muy pequeña comparada con la presión atmosférica. Por tanto, podemos considerar la densidad del aire no cambia (fluido incompresible) cuando pasa de una pompa a la otra.

La diferencia de presión entre las esferas de radio R₁ y de radio R₂ serán

$p_{2} - p_{1} = 4 γ (\frac{1}{R_{2}} - \frac{1}{R_{1}})$

Como consecuencia de la diferencia de presión, el aire circula por el tubo de comunicación con una velocidad dada por el teorema de Bernoulli

$p_{2} - p_{1} = \frac{1}{2} ρ v^{2}$

El volumen de aire que pasa de la segunda esfera a la primera en el tiempo dt es vSdt, siendo S=πr² la sección del tubo que comunica ambas esferas. ρ=1.29 kg/m³ es la densidad del aire

El volumen de la primera esfera aumenta, y el de la segunda disminuye.

$\begin{array}{l} d V_{1} = S v \cdot d t \\ 4 π R_{1}^{2} d R_{1} = S \sqrt{\frac{4 γ (R_{1} - R_{2})}{ρ R_{1} R_{2}}} d t \end{array}$

Hay que resolver la integral por procedimientos numéricos

$\int_{R_{01}}^{R_{1}} \frac{x^{2} d x}{\sqrt{{(V - x^{3})}^{- 1 / 3} - 1 / x}} = \frac{r^{2}}{4} \sqrt{\frac{4 γ}{ρ}} t V = R_{01}^{3} + R_{02}^{3} = R_{1}^{3} + R_{2}^{3}$

Conocido el radio inicial de la esfera izquierda, R₀₁ se calcula el tiempo t cuando dicha esfera alcanza el radio R₀₁≤R₁<V^1/3

La última ecuación, indica que la suma de los volúmenes de las dos esferas es constante. Podemos considerar en esta aproximación el aire como un fluido incomprensible, ya que los cambios de presión que experimenta en el interior de las burbujas son muy pequeños, comparados con la presión atmosférica.

Nota: La descripción dada en este párrafo, se debe de entender desde el punto de vista cualitativo, explica el fenómeno observado de que dos globos o dos pompas de jabón conectadas por un pequeño tubo de volumen despreciable, la esfera de mayor radio aumenta a costa de la de menor radio, hasta que esta última desaparece. Un análisis termodinámico del problema es demasiado complicado para incluirlo en estas páginas, se puede consultar el segundo artículo citado en las referencias.

Actividades

Se introduce

el radio inicial de cada una de las esferas, actuando en las barras de desplazamiento tituladas Radio burbuja. En la parte izquierda, se representa la esfera de mayor radio.
el valor para la tensión superficial de la pompa de jabón comprendido entre 20·10^-3 y 80·10^-3 N/m, en el control de edición titulado Tensión superficial.
El radio del tubo de comunicación se ha fijado en r=0.5 cm

Se pulsa el botón titulado Empieza

Observamos como la burbuja pequeña se hace cada vez más pequeña mientras crece la burbuja grande.

CalibreApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Pellicer, J, García-Morales V., Hernández M. J., On the demostration of Young-Laplace equations in introductory courses. Phys. Educ 35 (2) March 2000, pp. 126-129.

Weinhaus F., Barker W. On the equilibrium states of interconnected bubbles o balloons. Am. J. Phys. 46 (10) October 1978, pp. 978-982.