Variación de la velocidad del sonido con la temperatura
La velocidad del sonido en un gas no es constante, sino que depende de la temperatura.
De la ecuación de un gas ideal pV=nRT o bien,
La fórmula de la velocidad del sonido se expresa en función de la temperatura t del gas en grados centígrados.
Para obtener esta expresión aproximada, se han tomado los dos primeros términos del desarrollo de (1+t/T0)1/2 por el binomio de Newton
Sabiendo que T0=273.15 K, γ=1.4, R=8.314 J/(K·mol) y M=28.95·10-3 kg/mol, tenemos que
vs≈331.4+0.61·t
donde 331.4 m/s es la velocidad del sonido en el aire a 0ºC.
Para temperaturas cercanas a la ambiente, la velocidad del sonido en el aire varía aproximadamente de forma lineal con la temperatura.
El applet que viene a continuación, simula un experimento de medida de la velocidad del sonido a diferentes temperaturas. Consta de dos tubos coaxiales, de longitud L, el interior contiene aire y por el exterior circula agua a temperatura t procedente de un termostato. Un altavoz se coloca en el extremo del tubo interior y en el otro extremo un micrófono. El altavoz se conecta a un generador de sonido aleatorio, por ejemplo, a una radio que no sintoniza ninguna emisora concreta. El micrófono se conecta a un ordenador para analizar la señal que llega al extremo opuesto del tubo.
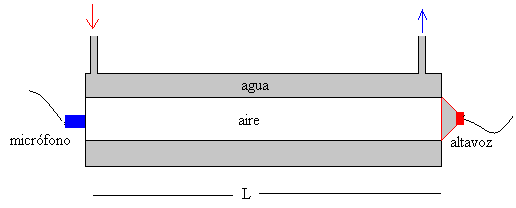
Las ondas estacionarias de un tubo abierto por ambos extremos o de una cuerda de longitud L sujeta por ambos extremos, tienen las siguientes frecuencias
Midiendo la frecuencia fn de un determinado armónico n se puede obtener la velocidad del sonido vs, tal como hemos visto en la actividad anterior.
El ruido tiene un espectro continuo de frecuencias, y el tubo actúa como un filtro que selecciona sus frecuencias de resonancia, tal como se aprecia en la figura.
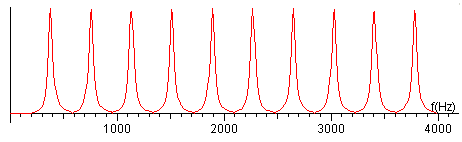
La señal recibida por el micrófono, se analiza en un ordenador, que determina las frecuencias correspondientes a los máximos de intensidad.
Para determinar la velocidad del sonido en el aire para una temperatura t dada, se representa gráficamente las frecuencias de resonancia fn en función de n. La pendiente de la recta que mejor ajusta es vs/(2L). Conocido el valor de L=45 cm, se calcula la velocidad del sonido vs.
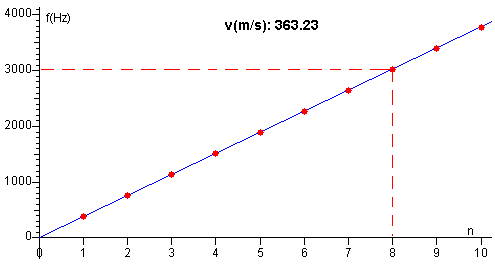
Una vez que disponemos de suficientes pares de datos, (temperatura en grados centígrados, velocidad del sonido), representamos los “datos experimentales” y observamos que se ajustan aproximadamente a la recta
vs=331.4+0.61·t
Actividades
Se pulsa el botón titulado Nuevo
-
Se introduce la temperatura t en grados centígrados, actuando sobre la barra de desplazamiento titulada Temperatura
Se pulsa el botón titulado Espectro
El tubo cerrado por ambos extremos actúa como un filtro que selecciona sus frecuencias de resonancia. En la pantalla del “ordenador”, se representa la intensidad del sonido que llega al micrófono en función de la frecuencia f en el intervalo comprendido entre 0 y 4000 Hz.
Se “mide” la frecuencia fn de los máximos de intensidad.
Se pulsa el botón titulado Velocidad
Se representa la frecuencia fn en función del número n de armónico.
Se mide la pendiente de la recta que mejor “ajusta”. Conocida la longitud L=45 cm del tubo, se calcula la velocidad del sonido vs.
vs=pendiente·2·0.45 m/s
Los pares de datos,
-
temperatura t en grados centígrados
-
velocidad del sonido vs
se guardan en el control área de texto, situado a la izquierda del applet.
Cuando tengamos suficientes datos “experimentales” se pulsa el botón titulado Gráfica. Para representar dichos datos junto a la recta
vs=331.4+0.61·t
Referencias
Velasco S., Román F.L., González A, White J. A., A computer-assisted experiment for the measurement of the temperature dependence of the speed of sound in air. Am. J. Phys. 72 (2) February 2004, pp. 276-279.
