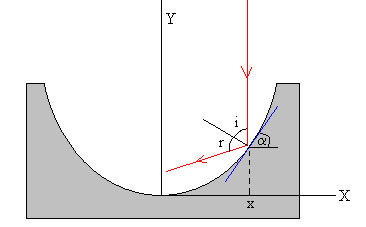
Reflexión en espejos.

Sea la curva y=f(x). El ángulo α que forma la recta tangente a la curva en el punto de abscisa x, vale

$\tan α = \frac{d y}{d x} = f' (x)$

Como vemos en la figura el ángulo de incidencia i =α, y por la ley de la reflexión, r=α

Espejo parabólico

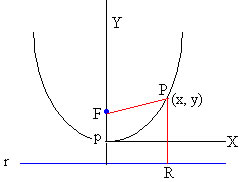
Sea F un punto y r una recta, tal que F no pertenece a r. Se denomina parábola de foco F y directriz r a la figura formada por todos los puntos (x, y) del plano que equidistan de F y r. La distancia del foco a la directriz se denomina parámetro p de la parábola

La ecuación de la parábola se calcula del siguiente modo: La distancia de F a P es igual a la distancia entre P y R

$\begin{array}{l} x^{2} + {(y - \frac{p}{2})}^{2} = {(y + \frac{p}{2})}^{2} \\ y = \frac{1}{2 p} x^{2} \end{array}$

Esta es la ecuación de la parábola. La pendiente de la recta tangente en el punto de abscisa x es

$\tan α = \frac{x}{p}$

Vamos a demostrar que todos los rayos reflejados en la superficie parabólica pasan por el foco F.

El rayo reflejado está contenido en la recta que pasa por el punto $(x, \frac{x^{2}}{2 p})$ y forma un ángulo de 90+2α con el eje X. La ecuación de esta recta es y’=ax’+b

$a = \tan (90 + 2 α) = \frac{\tan^{2} α - 1}{2 \tan α} = \frac{x^{2} - p^{2}}{2 p x}$

El parámetro b se determina a partir de la condición de que la recta pasa por dicho punto

$\begin{array}{l} y' = \frac{x^{2} - p^{2}}{2 p x} x' + b \\ \frac{x^{2}}{2 p} = \frac{x^{2} - p^{2}}{2 p x} x + b b = \frac{p}{2} \end{array}$

La recta

$y' = \frac{x^{2} - p^{2}}{2 p x} x' + \frac{p}{2}$

Pasa por el punto (0, p/2) que es el foco F de la parábola

Espejo esférico

Si cambiamos la parábola por un arco de circunferencia, los rayos ya no convergen en un punto.