Oscilaciones anarmónicas

La energía potencial de un muelle real no tiene por que ser simétrica, E_p=kx²/2, tal como hemos estudiado. De hecho en la página "Movimiento Armónico Simple" comparamos el movimiento de una partícula en dicho potencial simétrico con otra partícula que se mueve en el potencial de Morse. El objetivo era que el lector diferenciase entre un M.A.S. de un movimiento oscilatorio en general.

En esta página estudiamos el oscilador anarmónico y explicaremos cualitativamente el fenómeno de la dilatación de los sólidos cuando se calientan.

Partícula unida a un muelle no ideal

Vamos a estudiar el movimiento de una partícula a lo largo del eje X cuando su energía potencial está definida por la función

$E_{p} (x) = \frac{1}{2} k x^{2} - \frac{1}{3} s k x^{3}$

Donde s se denomina constante de anarmonicidad. Cuando s=0, tenemos el conocido potencial simétrico de una partícula unida a un muelle ideal de constante k.

Energía

La energía total de la partícula en una posición x es la suma de la energía cinética y potencial

E=E_k+E_p(x)

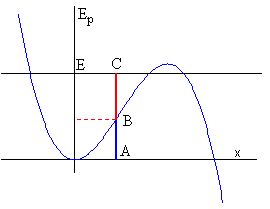
En la figura el segmento AC representa la energía total E, el segmento AB la energía potencial y el BC la energía cinética.

Como la energía cinética no puede ser negativa, las abscisas de los dos puntos de intersección entre la recta horizontal (color negro) que señala la energía total constante E con la función E_p(x) (en color azul) marca los límites del movimiento de la partícula.

La energía potencial de la partícula es máxima en los dos puntos más alejados del origen, y es mínima en x=0, (posición de equilibrio). Lo contrario le ocurre a la energía cinética que es mínima (cero) en los dos puntos más alejados del origen y es máxima en el origen.

Fuerza

La fuerza sobre la partícula debida al muelle no ideal será

$F = - \frac{d E_{p}}{d x} = - k x + s k x^{2}$

A la izquierda del origen x<0, la pendiente de la función E_p es negativa, la fuerza es positiva (hacia la derecha). A la derecha del origen x>0 la pendiente de la curva es positiva, la fuerza es negativa (hacia la izquierda).

Las posiciones de equilibrio en las que F=0 son x=0, y x=1/s la función E_p(x) presenta un mínimo y un máximo respectivamente.

La derivada segunda de la función energía potencial es

$\frac{d E_{p}^{2}}{d x^{2}} = k - 2 s k x$

Cuando x=0, la derivada segunda es positiva, tenemos un mínimo en la función energía potencial E_p(x) o posición de equilibrio estable.
Cuando x=1/s, la derivada segunda es negativa, tenemos un máximo relativo en la función energía potencial E_p(x) o posición de equilibrio inestable. El valor del máximo es

$x = \frac{1}{s} E_{p} = \frac{1}{6} \frac{k}{s^{2}}$

Vamos a estudiar las oscilaciones de una partícula unida a un muelle no ideal en torno a la posición de equilibrio estable x=0.

Ecuación del movimiento

La ecuación del movimiento es

ma=-kx+skx²

o en forma de ecuación diferencial

$\frac{d^{2} x}{d t^{2}} + ω_{0}^{2} x - ω_{0}^{2} s x^{2} = 0 ω_{0}^{2} = \frac{k}{m}$ (1)

ω₀ es la frecuencia angular propia de una partícula de masa m unida al muelle ideal de constante k.

Se ha resuelto la ecuación diferencial mediante el procedimiento numérico de Runge-Kutta, con las siguientes condiciones iniciales. En el instante t=0, la posición inicial de la partícula es x₀ (a la derecha del origen) y su velocidad inicial es v₀=0.

En la posición inicial, la energía cinética de la partícula es cero y por tanto, la energía potencial es igual a la energía total. Dada la energía total E de la partícula, podemos hallar la posición inicial x₀. Para ello, hay que resolver la ecuación cúbica.

$E = \frac{1}{2} k x^{2} - \frac{1}{3} s k x^{3}$

Si el valor de E es menor que el máximo, la raíz de la ecuación cúbica se encuentra en el intervalo comprendido entre x=0 y x=1/s.

Posición media

Si la energía potencial fuese simétrica, la partícula describiría una elipse en el espacio de las fases (x, v). Debido a que ya no es simétrica la trayectoria de la partícula en el espacio de las fases está deformada, tal como podemos ver en la parte superior izquierda del applet.

Cuando la energía total es próxima al mínimo, la partícula describe aproximadamente un M.A.S. La trayectoria en el espacio de las fases es aproximadamente una elipse. Si la energía total de la partícula es próxima a su valor máximo, se observa una trayectoria en el espacio de las fases que se asemeja a una elipse deformada. La partícula pasa gran parte del tiempo que emplea en completar la trayectoria en la región x>0.

La posición media <x> de una partícula que describe un M.A.S. viene dada por la integral

$< x > = \frac{1}{P} \int_{0}^{P} A \sin (ω t + ϕ) d t$

que como puede comprobarse fácilmente vale cero <x>=0. En el caso de una partícula unida a un muelle no ideal <x>≠0. La posición media <x> estará situada a la derecha del origen ya que la partícula pasa más tiempo a la derecha que a la izquierda del origen.

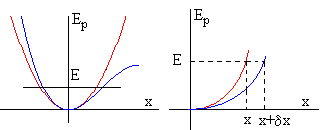
La curva de color rojo representa la energía potencial E_p(x)=kx²/2 (parábola), y la curva en color azul la energía potencial

$E_{p} (x) = \frac{1}{2} k x^{2} - \frac{1}{3} s k x^{3}$

Una partícula cuya energía total es E, oscila entre las abscisas de los puntos de intersección de la recta E_p(x)=E y la curva de energía potencial.

Para el potencial armónico (curva de color rojo), como ya hemos demostrado, la posición media de la partícula es el origen <x>=0, al ser la curva simétrica. Para el potencial descrito por la curva de color azul, la posición media está desviada δx hacia la derecha tal como se ve en la figura.

Podemos calcular δx, fijándonos en la parte derecha de la figura en la que se ha amplificado la parte izquierda.

$\begin{array}{l} E = \frac{1}{2} k x^{2} = \frac{1}{2} k {(x + δ x)}^{2} - \frac{1}{3} k s {(x + δ x)}^{3} \\ \frac{1}{2} k x^{2} \approx \frac{1}{2} k (x^{2} + 2 x δ x) - \frac{1}{3} k s (x^{3} + 3 x^{2} δ x) \\ δ x = \frac{1}{3} \frac{s}{(1 - k s)} x^{2} \approx \frac{1}{3} s x^{2} \end{array}$

Como la energía E=kx²/2 es del orden de k_BT. Siendo k_B la constante de Boltzmann (no confundir con la constante k del potencial armónico) y T la temperatura absoluta, llegamos a la expresión para δx

$δ x = \frac{2}{3} \frac{s}{k} k_{B} T$

El valor medio de la posición x de una partícula que se mueve bajo la acción de una fuerza cuya energía potencial es de la forma E_p(x)=kx²/2-ksx³/3 es proporcional a la temperatura T, y depende del cociente s/k. El valor medio es cero para las oscilaciones armónicas, s=0.

Actividades

En el programa interactivo, se introducen los dos parámetros que describen el sistema formado por una partícula unida a un muelle no ideal.

La constante elástica k del muelle en el control de edición titulado Constante elástica.
La constante de anarmonicidad s, en el control de edición titulado Anarmonicidad.
La masa de la partícula se ha fijado en la unidad m=1.

Se pulsa el botón titulado Nuevo

Se representa la función energía potencial E_p(x) en la parte derecha del applet.

Como podemos apreciar, cambiando los valores de la constante elástica k y de la constante de anarmonicidad s, obtenemos diversas formas de la curva de energía potencial.

Se introduce la energía total E de la partícula en el control de edición titulado Energía.

Se pulsa el botón titulado Empieza

Si la energía E es mayor que la máxima (para x=1/s) el programa no prosigue, el foco regresa al control de edición para que el usuario introduzca un valor menor de la energía.

En el applet se puede observar tres zonas:

A la derecha, la representación de la función energía potencial E_p(x). Los valores de la energía cinética y potencial de la partícula representados por barras de color rojo y azul.
En la parte inferior izquierda, el movimiento de la partícula unida a un muelle elástico no ideal. Se representa mediante una flecha la fuerza sobre la partícula.
En la parte superior izquierda, se representa la trayectoria de la partícula en el espacio de las fases.

ForzadasApplet aparecerá en un explorador compatible con JDK 1.1.

Solución analítica. Dilatación de los sólidos

Probemos una solución de la ecuación diferencial del movimiento (1) de la forma

x=x₁+A(cos(ω t)+q cos(2ω t))

donde q y x₁ son constantes a determinar.

Introducimos la solución en la ecuación diferencial y suponiendo que sA<<1, llegamos a las siguientes conclusiones (véase la referencia al final de esta página):

La condición de que el coeficiente de cos(ω t) se anule es

ω =ω₀

La condición de que el coeficiente de cos(2ω t) se anule es

q=-sA/6

El desplazamiento x₁ viene dado por

x₁=sA²/2

El valor medio de la posición de la partícula

<x>=x₁+A(<cos(ω t)>+q <cos(2ω t)>)

Los valores medios de las funciones armónicas son cero, quedando

$< x > = \frac{1}{2} s A^{2}$

Teniendo en cuenta que:

La energía de un oscilador es proporcional al cuadrado de su amplitud A
Uno de los resultados de la Física Estadística es que la energía media de un oscilador armónico clásico en equilibrio térmico es igual a kT, siendo k la constante de Boltzmann y T la temperatura absoluta.

Concluimos que, la posición media es proporcional a la temperatura T.

<x>=cte·T

Este resultado explica la dilatación térmica de los sólidos. El incremento de longitud de una varilla metálica cuando es calentada es proporcional al incremento de la temperatura.

l=l₀(1+α ·ΔT)

siendo l₀ la longitud inicial de la varilla, α el coeficiente de dilatación térmica, y ΔT el incremento de temperatura.

Aparato para la medida de la dilatación de una varilla metálica. Laboratorio de Física. E. U. Ingeniería Técnica de Minas y Obras Públicas (Barakaldo).

Referencias

Kittel, Knight, Ruderman. Mecánica, Berkeley Physics Course. Edt. Reverté (1973). Págs. 227-229.