Oscilaciones de una partícula bajo la acción de dos muelles elásticos

En esta página se estudia el caso en el que la energía potencial E_p(x) se puede desarrollar en serie alrededor de la posición de equilibrio estable, pero el término cuadrático es nulo y la serie comienza con un término superior al de segundo orden.

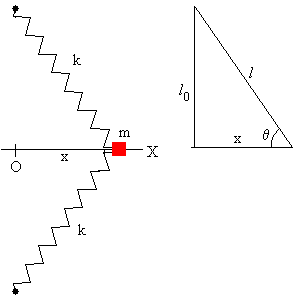Sea un bloque de masa m unido a dos muelles elásticos iguales de constante k. La longitud de los muelles si deformar es l₀, cuando el sistema está en la posición de equilibrio estable x=0.

Cuando se separa el bloque una distancia x de la posición de equilibrio y se suelta, empieza a oscilar con un periodo P.

Ecuación del movimiento

La fuerza F que ejerce cada uno de los muelles sobre el bloque es

$F = k (\sqrt{x^{2} + l_{0}^{2}} - l_{0})$

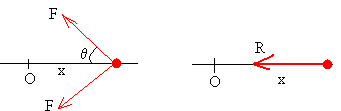
La resultante es

$R = 2 F \cos θ = 2 F \frac{x}{\sqrt{x^{2} + l_{0}^{2}}} = 2 k (1 - \frac{l_{0}}{\sqrt{x^{2} + l_{0}^{2}}}) x$

La ecuación del movimiento es

$m \frac{d^{2} x}{d t^{2}} = - 2 k (1 - \frac{l_{0}}{\sqrt{x^{2} + l_{0}^{2}}}) x$

Esta ecuación, se resuelve aplicando procedimientos numéricos con las condiciones iniciales siguientes: en el instante inicial t=0, x=A, y v=dx/dt=0, siendo A la amplitud de la oscilación.

Periodo de las oscilaciones

Si E es la energía total de la partícula de masa m en una región donde la energía potencial está descrita por la función E_p(x). El principio de conservación de la energía se escribe

$\begin{array}{l} \frac{1}{2} m {(\frac{d x}{d t})}^{2} + E_{p} (x) = E \\ d t = \pm {(\frac{m}{2 E})}^{1 / 2} \frac{d x}{\sqrt{1 - E_{p} (x) / E}} \end{array}$

El periodo es cuatro veces el tiempo que tarda en moverse el bloque desde el origen hasta la posición de máximo desplazamiento o amplitud A.

Para obtener el periodo P de la oscilación hay que resolver la integral

$P = 4 {(\frac{m}{2 E})}^{1 / 2} \int_{0}^{A} \frac{d x}{\sqrt{1 - E_{p} (x) / E}}$

La velocidad del bloque en la posición de máximo desplazamiento es v=dx/dt=0. La amplitud A se calcula, resolviendo la ecuación trascendente E_p(A)=E

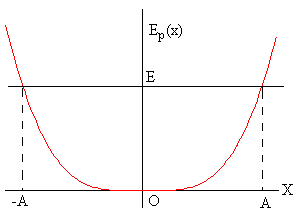
La energía potencial del bloque de masa m unido a los dos muelles elásticos es

$E_{p} (x) = 2 \cdot \frac{1}{2} k {(\sqrt{x^{2} + l_{0}^{2}} - l_{0})}^{2} = k l_{0}^{2} {(\sqrt{1 + {(x / l_{0})}^{2}} - 1)}^{2}$

Desarrollamos en serie la función

$\begin{array}{l} f (u) = {(\sqrt{1 + u} - 1)}^{2} u = x^{2} / l_{0}^{2} \\ f (u) = f (0) + {(\frac{d f}{d u})}_{0} u + \frac{1}{2!} {(\frac{d^{2} f}{d u^{2}})}_{0} u^{2} + \frac{1}{3!} {(\frac{d^{3} f}{d u^{3}})}_{0} u^{3} + . .. = \\ \frac{1}{2!} (\frac{1}{2}) u^{2} - \frac{1}{3!} (\frac{- 3}{4}) u^{3} + ... \end{array}$

Para pequeñas oscilaciones u<<1 o x<<l₀ solamente el primer término es importante

$E_{p} (x) = k l_{0}^{2} f (u) \approx (\frac{k}{4 l_{0}^{2}}) x^{4}$

La fórmula del periodo se escribe

$P = \frac{4}{A^{2}} {(\frac{2 m l_{0}^{2}}{k})}^{1 / 2} \int_{0}^{A} \frac{d x}{\sqrt{1 - x^{4} / A^{4}}}$

Haciendo el cambio de variable

$x = A \cdot {sin}^{1 / 2} θ$

Llegamos a la integral

$P = 2 \sqrt{2} \frac{l_{0}}{A} \sqrt{\frac{m}{k}} \int_{0}^{π / 2} {sen}^{- 1 / 2} d θ$

Esta integral se expresa en términos de la función Г de Euler. El resultado es (véase el artículo citado en las referencias)

$P = 7.4163 \cdot \frac{l_{0}}{A} \sqrt{\frac{m}{k}}$

Actividades

Se introduce

El valor del cociente k/m actuando en la barra de desplazamiento titulada Cociente.
La longitud del muelle sin deformar se ha fijado en el programa interactivo en el valor l₀=1

Se pulsa el botón titulado Inicio

Se desplaza con el puntero del ratón la partícula a una posición inicial A, de la que parte la partícula con velocidad inicial nula.

Se pulsa el botón titulado Empieza

La ecuación del movimiento de la partícula se resuelve por procedimientos numéricos, para cualquier valor de la amplitud A comprendida entre 0 y 1.0.

A la derecha del applet, se representa la energía potencial E_p(x). La recta horizontal es la energía total, y la recta vertical está dividida en dos porciones de color rojo y azul, la primera representa la energía potencial y la segunda, la energía cinética. También, se representa mediante una flecha la fuerza sobre la partícula.

Ejemplo 1:

Sea k=60, m=1 y la amplitud A=0.3

La longitud de cada uno de los dos muelles sin deformar es l₀=1.0

La energía total del oscilador es

$E = E_{p} (A) = 60 {(\sqrt{1^{2} + {0.3}^{2}} - 1)}^{2} = 0.12$

La energía total E en la aproximación de pequeñas oscilaciones es

$E = \frac{60}{4 \cdot 1^{2}} {0.3}^{4} = 0.12$

El periodo P en la aproximación de oscilaciones de pequeña amplitud es

$P = 7.4163 \cdot \frac{1.0}{0.3} \frac{1}{\sqrt{60}} = 3.19$

El programa interactivo nos proporciona el valor de P=3.22 a partir de la resolución de la ecuación diferencial del movimiento por procedimientos numéricos.

Ejemplo 2:

Sea k=60, m=1 y la amplitud A=0.7

La energía total del bloque es

$E = E_{p} (A) = 60 {(\sqrt{1^{2} + {0.7}^{2}} - 1)}^{2} = 2.92$

La energía total E en la aproximación de pequeñas oscilaciones es

$E = \frac{60}{4 \cdot 1^{2}} {0.7}^{4} = 3.60$

El periodo P en la aproximación de oscilaciones de pequeña amplitud es

$P = 7.4163 \cdot \frac{1.0}{0.7} \frac{1}{\sqrt{60}} = 1.37$

El programa interactivo nos proporciona el valor de P=1.55 a partir de la resolución de la ecuación diferencial del movimiento por procedimientos numéricos.

LibresApplet aparecerá en un explorador compatible con JDK 1.1.

Mueva con el puntero del ratón el cuadrado de color rojo