El péndulo forzado

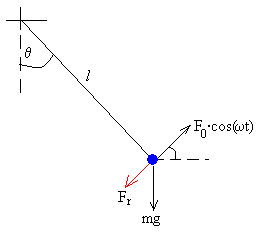Supongamos un péndulo simple, sobre el que actúa una fuerza externa tangencial sinusoidal y una fuerza de rozamiento proporcional a la velocidad.

La ecuación del movimiento es

$\begin{array}{l} m l \frac{d^{2} θ}{d t^{2}} = F_{0} \cos (ω t) - β l \frac{d θ}{d t} - m g \sin θ = 0 \\ \frac{d^{2} θ}{d t^{2}} + 2 γ \frac{d θ}{d t} + ω_{0}^{2} \sin θ = f \cos (ω t) \end{array}$

Donde ω₀ es la frecuencia propia del péndulo y ω es la frecuencia angular de la fuerza aplicada.

Se resuelve la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, θ=x₀, dθ/dt=v₀.

Actividades

Se introduce

La amplitud del momento exterior f, en el control de edición titulado Amplitud.
La frecuencia angular ω del momento exterior, en el control de edición titulado Frecuencia.
La constante de proporcionalidad 2γ del momento de la fuerza de rozamiento. En el control de edición titulado 2·gamma.
La posición angular inicial θ₀ y la velocidad angular inicial (dθ/dt)₀ en los controles de edición titulados x₀, v₀.
Se ha fijado la frecuencia propia o natural del oscilador en ω₀=1.

Seleccionado el botón de radio titulado:

Péndulo, se muestra el movimiento del péndulo y las fuerzas que actúan sobre la masa puntual excepto la tensión de la cuerda ya que no contribuye el movimiento en la dirección tangencial.
Grafica x-t, se traza la gráfica de la posición angular del péndulo θ en función del tiempo t.
Gráfica x-v, en el espacio de las fases cuyo eje horizontal es la posición θ y cuyo eje vertical es la velocidad dθ/dt.

Se pulsa el botón titulado Empieza.

A pesar de la simplicidad del péndulo, este sistema presenta una gran variedad de comportamientos, que se pueden visualizar mediante el siguiente programa interactivo. Para una descripción más detallada del péndulo forzado, se sugiere la lectura del artículo de Butikov mencionado en las referencias

ForzadasApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Landau R. H., Páez M. J. Computational Physics. Problem solving with computers. John Wiley & Sons (1997), pp. 182, 188-190.

Butikov E. I. Extraordinary oscillations of an ordinary forced pendulum. Eur. J. Phys. 29 (2008) 215-233