• Inicio
• Oscilaciones
• Osciladores no lineales

El péndulo

En el capítulo de Sólido rígido estudiamos las oscilaciones pequeñas de un péndulo compuesto. En esta página, vamos a estudiar el comportamiento general de un péndulo, para pequeñas y grandes amplitudes, e incluso cuando el péndulo da vueltas.

La ecuación diferencial que describe el comportamiento del péndulo compuesto es

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{mgb}{I_0}\sin \theta =0}$          (1)

Cuando el ángulo θ  es pequeño entonces, sinθ ≈θ . El péndulo describe un M.A.S. cuyo periodo P₀ es

${\displaystyle P_0=2\pi \sqrt{\frac{I_0}{mgb}}}$

Se resuelve la ecuación diferencial de segundo orden

${\displaystyle \frac{d^2\theta }{d{t}^2}+{\omega }^2\sin \theta =0}$

por procedimientos numéricos con las condiciones iniciales: t=0, dθ/dt=0, θ=θ₀

El periodo del péndulo

Supongamos que el péndulo está en la posición de equilibrio estable, y le proporcionamos una energía E.

El péndulo adquiere una velocidad inicial ω₀. A medida que se desplaza un ángulo θ  la energía cinética de rotación se convierte en energía potencial, hasta que alcanza una desviación máxima θ₀ cuando ω =0. Luego, se realiza el proceso inverso, la energía potencial se convierte en energía cinética de rotación, hasta que al pasar de nuevo por la posición de equilibrio θ =0, toda la energía potencial se ha convertido en cinética, la velocidad angular del péndulo será -ω₀. A continuación, el péndulo alcanza de nuevo la desviación máxima -θ₀, y finalmente, regresa a la posición de equilibrio estable completándose la oscilación.

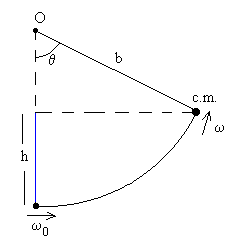
El principio de conservación de la energía establece que la suma de la energía cinética de rotación del péndulo más potencial es constante. La energía potencial del centro de masa del sólido rígido tal como vemos en la figura vale

mgh=mgb(1-cosθ ).

b es la distancia entre el centro de masa (c.m.) y el eje de rotación O del sólido rígido

${\displaystyle E=\frac{1}{2}{I}_0{\omega }^2+mgb\left(1-\cos \theta \right)}$

Cuando el péndulo alcanza la máxima desviación ω=0, y E=mgb(1-cosθ₀)

${\displaystyle \begin{array}{l}mgb(1-\cos {\theta }_0)=\frac{1}{2}{I}_0{\left(\frac{d\theta }{dt}\right)}^2+mgb\left(1-\cos \theta \right)\\ {\left(\frac{d\theta }{dt}\right)}^2=\frac{4mgb}{I_0}\left({\sin }^2\frac{\theta }{2}-{\sin }^2\frac{{\theta }_0}{2}\right)\end{array}}$

Despejando el tiempo dt en la ecuación diferencial

${\displaystyle dt=\sqrt{\frac{mgb}{I_0}}\frac{d\frac{\theta }{2}}{\sqrt{{\sin }^2\frac{{\theta }_0}{2}-{\sin }^2\frac{\theta }{2}}}}$

Sustituyendo

${\displaystyle \begin{array}{l}\sin \varphi =\frac{\sin \frac{\theta }{2}}{\sin \frac{{\theta }_0}{2}}k=\sin \frac{{\theta }_0}{2}\\ \frac{\theta }{2}=\arcsin (k·\sin \varphi )\frac{d\theta }{2}=\frac{k\cos \varphi ·d\varphi }{\sqrt{1-k^2{\sin }^2\varphi }}\end{array}}$

resulta

${\displaystyle dt=\sqrt{\frac{mgb}{I_0}}\frac{d\varphi }{\sqrt{1-k^2{\sin }^2\varphi }}}$

Integramos

${\displaystyle t=\sqrt{\frac{mgb}{I_0}}{\displaystyle \underset{0}{\overset{\varphi }{\int }}\frac{d\varphi }{\sqrt{1-k^2{\sin }^2\varphi }}}}$

Cuando el péndulo alcanza la desviación máxima θ =θ₀ o bien, cuando φ =π /2, ha empleado un cuarto del periodo P de la oscilación completa.

El periodo P de una oscilación lo podemos escribir

${\displaystyle P=\frac{2P_0}{\pi }{\displaystyle \underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{d\varphi }{\sqrt{1-k^2{\sin }^2\varphi }}}k=\sin \frac{{\theta }_0}{2}}$

donde P₀ es el periodo de las oscilaciones de pequeña amplitud.

La integral se denomina elíptica completa de primera especie. El programa interactivo que viene a continuación calcula el cociente P/P₀ cuando introducimos la amplitud θ₀ de la oscilación. El cálculo se basa en el procedimiento de Carlson para hallar la integral elíptica de primera especie denominada R_F(x, y, z). Véase Numerical Recipes in C, Special functions. Capítulo 6º

Programa para calcular el periodo de un péndulo para cualquier amplitud

ForzadasApplet aparecerá en un explorador compatible con JDK 1.1.

Desarrollo en serie

Desarrollamos en serie el denominador de la integral elíptica

${\displaystyle {(1-k^2{\sin }^2\varphi )}^{-1/2}=1+\frac{1}{2}{k}^2{\sin }^2\varphi +\frac{3}{8}{k}^4{\sin }^4\varphi +\mathrm{...}}$

La integral se convierte en

${\displaystyle {\displaystyle \underset{0}{\overset{\pi /2}{\int }}\left(1+\frac{1}{2}{k}^2{\sin }^2\varphi +\frac{3}{8}{k}^4{\sin }^4\varphi +\mathrm{...}\right)}d\varphi =\frac{\pi }{2}+\frac{1}{2}{k}^2\frac{\pi }{4}+\frac{3}{8}{k}^4\frac{3\pi }{16}+\mathrm{...}}$

Para resolver las integrales se utilizan las relaciones trigonométricas siguientes:

${\displaystyle {\sin }^2\theta =\frac{1-\cos (2\theta )}{2}{\cos }^2\theta =\frac{1+\cos (2\theta )}{2}}$

El desarrollo en serie del periodo P es

${\displaystyle P=P_0\left(1+\frac{1}{4}{\sin }^2\frac{{\theta }_0}{2}+\frac{9}{64}{\sin }^4\frac{{\theta }_0}{2}+\mathrm{...}\right)}$          (2)

Si la amplitud es pequeña  podemos escribir

${\displaystyle {\sin }^2\left(\frac{{\theta }_0}{2}\right)\approx \frac{{\theta }_0^2}{4}}$

y el periodo es, aproximadamente

${\displaystyle P\approx P_0\left(1+\frac{{\theta }_0^2}{16}\right)}$

Esta es la primera aproximación a la fórmula del periodo de un péndulo

La conclusión final, es que el periodo P crece con la amplitud θ₀. Mientras que el periodo P₀ es independiente de la amplitud siempre que la amplitud no sea muy grande y se pueda aplicar la aproximación senθ ≈θ.

Los primeros tres términos del desarrollo en serie se ajustan bien con los resultados experimentales para ángulos menores θ₀<50º. Para otros ángulos, se puede realizar una integración numérica por el método de Simpson.

Para simular el movimiento del péndulo para cualquier amplitud, se ha resuelto la ecuación diferencial de su movimiento (1), aplicando el procedimiento numérico de Runge-Kutta.

En la siguiente tabla se proporcionan

• En la primera columna, las medidas del periodo P/P₀ efectuadas en la simulación del movimiento del péndulo compuesto.
• En la segunda columna, son los resultados del cálculo del desarrollo en serie de la integral elíptica (2)
• En la tercera columna, los resultados del cálculo de la integral elíptica completa de primera especie

Ángulo	Periodo P/P0	Periodo P/P0	Periodo P/P0
π /6 (30º)	1.03	1.02	1.02
π /4 (45º)	1.05	1.03	1.04
π /3 (60º)	1.08	1.08	1.07
π /2 (90º)	1.19	1.19	1.18
2π /3 (120º)	1.38	1.35	1.37
3π /4 (135º)	1.53	1.42	1.53
5π /6 (150º)	1.76	1.48	1.76

Fórmulas aproximadas del periodo de un péndulo

Se conocen varias fórmulas aproximadas del periodo del péndulo para cualquier amplitud, que se pueden comparar con la expresión exacta

${\displaystyle \frac{P}{P_0}=\frac{2}{\pi }{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\varphi }{\sqrt{1-k^2{\sin }^2\varphi }}}d\varphi k=\sin \frac{{\theta }_0}{2}}$

Donde θ₀<π es la amplitud del péndulo

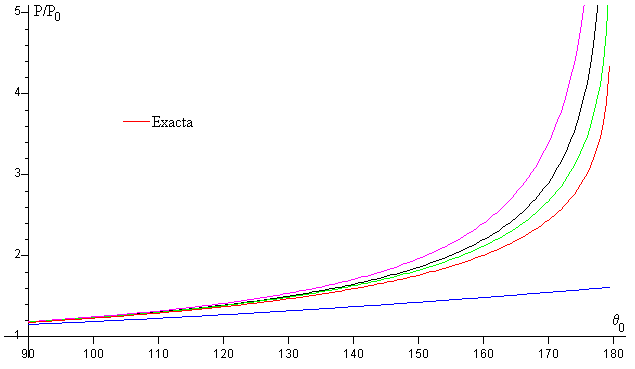
En la gráfica, se representa P/P₀ en función de la amplitud θ₀ en grados, curva de color rojo.

Esta integral elíptica completa de primera especie no se puede expresar en términos de funciones elementales.

1. La fórmula más sencilla, corresponde al desarrollo en serie antes mencionado, tomando los dos primeros términos y haciendo la aproximación senx≈x

${\displaystyle \frac{P}{P_0}\approx 1+\frac{{\theta }_0^2}{16}}$

La representación gráfica, corresponde a la curva de color azul, que observamos se aleja considerablemente de la solución exacta cuando la amplitud θ₀>90º

2. La fórmula (Kidd)

${\displaystyle \frac{P}{P_0}\approx \frac{1}{\sqrt{\cos ({\theta }_0/2)}}}$

La representación gráfica, corresponde a la curva de color rosa, que se aproxima mejor a la curva de color rojo.

3. La fórmula (Molina)

${\displaystyle \frac{P}{P_0}\approx {\left(\frac{{\theta }_0}{\text{sen}{\theta }_0}\right)}^{3/8}}$

La representación gráfica, corresponde a la curva de color negro, que se aproxima algo mejor que la anterior a la curva de color rojo.

4. La fórmula (Lima)

${\displaystyle \frac{P}{P_0}\approx -\frac{\ln (\cos ({\theta }_0/2))}{1-\cos ({\theta }_0/2)}}$

La representación gráfica, corresponde a la curva de color verde, que es la que mejor se aproxima a la curva de color rojo.

Curva de la energía potencial

Como ya hemos visto en este capítulo las curvas de energía potencial nos suministran información cualitativa acerca del comportamiento del sistema físico.

La energía potencial del péndulo es E_p=mgb(1-cosθ ). La energía potencial máxima del péndulo es 2mgb, cuando está en posición invertida. Representamos en la parte superior derecha del applet, el cociente de la energía potencial E_p entre la energía potencia máxima, en función del ángulo θ , es decir la función

${\displaystyle e_p=\frac{1}{2}\left(1-\cos \theta \right)}$

En estas unidades la energía potencial máxima es la unidad para θ =π , cuando el péndulo está invertido (posición de equilibrio inestable) y la mínima (cero) para θ =0, posición de equilibrio estable.

En dicho diagrama, representamos mediante una recta de color negro la energía total E, suma de la energía potencial y de la energía cinética. Un segmento vertical de color rojo señala la energía potencial del péndulo para la posición θ , y un segmento de color azul la energía cinética del péndulo en dicha posición. Los valores de la energía total, cinética y potencial se han dividido por la energía potencial máxima 2mgb.

El principio de conservación de la energía establece que la suma de la energía cinética y la energía potencial es constante. De modo que, la energía cinética es máxima cuando la energía potencial es mínima (cuando el péndulo pasa por la posición de equilibrio estable) y la energía cinética es mínima (cero) cuando el péndulo alcanza la desviación máxima.

El espacio de las fases

En el diagrama de fases representamos la velocidad angular ω (o el momento angular I₀·ω ) en función del desplazamiento angular θ.

Si el movimiento de un sistema físico es periódico el sistema vuelve al mismo estado después de un ciclo completo. La representación de su trayectoria en el espacio de las fases es una curva cerrada.

Para obtener la ecuación de dicha trayectoria basta escribir el principio de conservación de la energía

${\displaystyle E=\frac{1}{2}{I}_0{\omega }^2+mgb\left(1-\cos \theta \right)}$

Para una energía total dada E, esta ecuación nos relaciona la velocidad angular ω con el desplazamiento angular θ .

Observamos que la trayectoria en el espacio de las fases es simétrica respecto del eje vertical ω (de la velocidad angular). Esta simetría quiere decir, que el movimiento del péndulo es el mismo en el sentido de las agujas del reloj que en sentido contrario. Pueden ocurrir dos casos:

Oscilaciones

Que la energía total E del péndulo sea menor que el máximo valor de la energía potencia (E<2mgb) o bien (e<1). En el diagrama de la energía potencial vemos que la energía total es menor que la altura de la barrera de potencial. El péndulo oscila entre dos posiciones extremas θ₀ y -θ₀.

Esta amplitud la podemos calcular poniendo ω =0 en el principio de conservación de la energía.

E=2mgb(1-cosθ ₀)

${\displaystyle \sin \frac{{\theta }_0}{2}=\sqrt{\frac{E}{2mgb}}\text{sin}\frac{{\theta }_0}{2}=\sqrt{e}}$

Ejemplo: sea e=0.5 (energía en unidades de la energía potencial máxima) entonces θ₀=π /2=90º. Si e=0.1 entonces θ₀=36.9º

Si la amplitud es pequeña, el péndulo describe un Movimiento Armónico Simple y la trayectoria en el espacio de las fases se aproxima a una elipse.

${\displaystyle \begin{array}{l}1-\cos \theta =2{\sin }^2\frac{\theta }{2}\approx \frac{{\theta }^2}{2}\\ E\approx \frac{1}{2}{I}_0{\omega }^2+mgb\frac{{\theta }^2}{2}\\ \frac{{\omega }^2}{\frac{2E}{I_0}}+\frac{{\theta }^2}{\frac{2E}{mgb}}\approx 1\end{array}}$

Los denominadores de esta última expresión nos dan los cuadrados de los semiejes de la elipse. El semieje horizontal (máxima amplitud) vale

${\displaystyle {\theta }_0\approx \sqrt{\frac{2E}{mgb}}=\sqrt{4e}}$

A medida que se aumenta la energía, la trayectoria en el espacio de las fases se desvía de la forma elíptica y la oscilación deja de ser armónica. Como el péndulo pasa mucho más tiempo en las proximidades de su desviación máxima θ₀, la trayectoria en el espacio de las fases se hace más aguda en los extremos izquierdo y derecho, y más plana en la parte superior e inferior.

Rotaciones

Cuando la energía total E del péndulo es mayor que el máximo valor de la energía potencial (E>2mgb) o bien (e>1), el péndulo da vueltas completas.

El movimiento de rotación no es uniforme, la velocidad es máxima cuando pasa por la posición de equilibrio estable y es mínima cuando pasa por la posición de péndulo invertido. La posición angular del péndulo se incrementa continuamente y la velocidad angular es siempre positiva (si la rotación es en sentido contrario a las agujas del reloj).

El péndulo repite el mismo movimiento cuando su posición angular θ se incrementa en 2π , 4π , etc. Para describir este movimiento en el espacio de las fases, es suficiente con considerar la parte de dicho espacio comprendida entre -π y π . El punto que representa la posición y la velocidad angular del péndulo en el espacio de las fases sale de dicha región por la derecha y entra por la izquierda.

Periodo del péndulo

De la ecuación de la conservación de la energía despejamos la velocidad angular ω del péndulo

${\displaystyle \omega =\sqrt{\frac{2E-mgb(1-\cos \theta )}{I_0}}=\sqrt{\frac{2mgb}{I_0}}\sqrt{2e-1+\cos \theta }e=\frac{E}{2mgb}}$

El tiempo que tarda el péndulo en desplazarse entre las posiciones θ y θ+dθ es

${\displaystyle dt=\frac{d\theta }{\omega }=\sqrt{\frac{I_0}{2mgb}}\frac{d\theta }{\sqrt{2e-1+\cos \theta }}}$

El periodo P es

${\displaystyle P=\frac{P_0}{2\sqrt{2}\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\theta }{\sqrt{2e-1+\cos \theta }}}}$

El applet que viene a continuación calcula el cociente P/P₀ cuando se introduce la energía e>1 del péndulo, resolviendo la integral definida por el procedimiento numérico de Simpson.

ForzadasApplet aparecerá en un explorador compatible con JDK 1.1.

Trayectoria separatriz

Cuando la energía total del péndulo E=2mgb, (e=1) estamos en el caso límite. La trayectoria del punto representativo en el espacio de las fases está señalada en color rojo en la parte inferior derecha del applet y se denomina separatriz.

Poniendo E=2mgb en el principio de conservación de la energía, obtenemos la ecuación de la separatriz

${\displaystyle \begin{array}{l}2mgb=\frac{1}{2}{I}_0{\omega }^2+mgb\left(1-\cos \theta \right)\\ \omega =\pm 2\sqrt{\frac{mgb}{I_0}}\cos \frac{\theta }{2}\end{array}}$

La separatriz divide al espacio de las fases en regiones que corresponden a dos tipos distintos de movimiento.

Cuando el péndulo alcanza la posición θ =-π o θ =π , su velocidad angular ω =0, el péndulo se encuentra en un estado de equilibrio inestable, en la denominada posición invertida. Un pequeño desplazamiento en uno u otro sentido hace que el péndulo oscile con una amplitud muy próxima a π . Y un pequeño empuje hace que describa un movimiento de rotación. El péndulo como vemos en la siguiente tabla pasa mucho tiempo en la vecindad de la posición invertida y su periodo P se hace infinito para la energía E=2mgb (e=1).

Ángulo	Periodo P/P0
179	3.91
179.5	4.34
179.9	5.36
179.99	6.41

Actividades

Se introduce el valor de la energía total e en el control de edición titulado Energía. Este valor es el cociente entre la energía total del péndulo E y la energía potencial máxima 2mgb.

Se pulsa el botón titulado Empieza.

Se observa el movimiento del punto representativo en el espacio de las fases y la forma de la trayectoria que describe.

En la parte superior derecha del applet, podemos observar cómo cambia la energía cinética (línea gruesa de color azul) y la energía potencial (en color rojo) con la posición θ del péndulo.

En la parte superior izquierda del applet, se proporciona el valor del tiempo t en unidades de P₀ periodo del péndulo para pequeñas oscilaciones, y la amplitud θ₀ de las oscilaciones (e<1)

Con ayuda de los botones Pausa/Continua y Paso, podemos medir el periodo del péndulo para cualquier amplitud. Para una mayor exactitud se pueden medir cinco oscilaciones completas y dividir el tiempo total entre cinco para hallar el periodo P del péndulo en unidades de P₀.

ForzadasApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Butikov. E. The rigid pendulum -an antique but evergreen physical model. Eur. J. Phys. 20 (1999) pp. 429-441.

Molina M. I., Simple linearizations of the simple pendulum for any amplitude. The Physics Teacher, Vol 35, November 1997, pp. 489-490

Kidd R. B. Fogg S. L., A simple formula for the large-angle pendulum period. The Physics Teacher Vol 40, February 2002, pp. 81-83

Millet L. E., The large-angle pendulum period. The Physics Teacher, Vol 41, March 2003, pp. 162-163

Lima F.M. S., Arun P., An accurate formula for the period of a simple pendulum oscillating beyond the small angle regime. Am. J. Phys. 74 (10) October 2006, pp. 892-895.

Puig Adam P., Cálculo Integral. Editorial Biblioteca Matemática 1972, pág 97

Curso Interactivo de Física en Internet © Ángel Franco García