• Inicio
• Sólido rígido
• Conservación del momento angular

Movimiento de una pelota que rebota en dos paredes verticales.

En la página titulada “Rebotes elásticos de una pelota entre dos paredes paralelas horizontales” estudiamos la trayectoria del centro de una pelota que rebotaba elásticamente entre dos paredes paralelas horizontales y en ausencia de gravedad. En la página titulada “Una pelota que rebota en el suelo” hemos deducido la relación entre las velocidades de la pelota inmediatamente antes y después de su choque inelástico con una superficie horizontal. Para ello, se han introducido dos coeficientes de restitución: normal ε y tangencial β que dan cuenta de las pérdidas de energía de la pelota durante el choque.

En esta página, observaremos el movimiento de una pelota que rebota en dos paredes verticales paralelas teniendo en cuenta la acción de la gravedad sobre el movimiento del centro de la pelota.

Descripción del movimiento

El centro de la pelota parte del origen y se lanza con velocidad V_0x hacia la pared opuesta a la vez que gira con velocidad angular ω₀, alrededor de un eje que pasa por el centro y que es perpendicular al plano de la trayectoria.

Las dos paredes verticales paralelas forman un canal de anchura w+2R, siendo R el radio de la pelota. El máximo desplazamiento horizontal del centro de la pelota es w.

Tiro parabólico

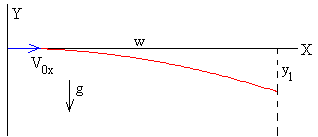
Las ecuaciones del movimiento del centro de la pelota son

${\displaystyle \begin{array}{l}{V}_{0y}=-gt\\ y=-\frac{1}{2}g{t}^{2}x=V_{0x}t\end{array}}$

La pelota choca con la pared derecha cuando su centro se desplaza w de modo que, la posición y velocidad de la pelota inmediatamente antes del primer choque son

${\displaystyle y=-\frac{1}{2}g{\left(\frac{w}{V_{0x}}\right)}^2{V}_{0y}=-g\left(\frac{w}{V_{0x}}\right)}$

La velocidad angular inicial de rotación ω₀ no se ve afectada por la gravedad.

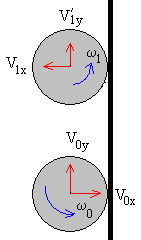
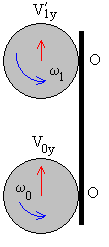
Choque inelástico con la pared derecha.

	La componente de la velocidad perpendicular a la pared cambia de módulo y sentido después del choque. ${\displaystyle V_{1x}=-\epsilon V_{0x}}$
	En el momento del choque, la fuerzas que ejerce la pared sobre la pelota (fuerza normal y fuerza de rozamiento) actúan en el punto de contacto O. Por lo que el momento angular de la pelota respecto de  dicho punto permanece constante. ${\displaystyle \begin{array}{l}-m{V}_{0y}R+I{\omega }_0=-mV{\text{'}}_{1y}R+I{\omega }_1\\ -V_{0y}+\gamma R{\omega }_0=-V{\text{'}}_{1y}+\gamma R{\omega }_1\\ V{\text{'}}_{1y}-V_{0y}=-\gamma R\left({\omega }_0-{\omega }_1\right)\end{array}}$
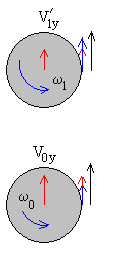	Para dar cuenta de las pérdidas de energía de la pelota durante el choque, en particular, el deslizamiento del punto de contacto sobre la superficie, se introduce el coeficiente de restitución tangencial β, de modo que las velocidades del punto de contacto O inmediatamente antes y después del choque están relacionadas. V’1y+ω1R=-β(V0y+ω0R)

Después del primer choque, obtenemos V_1x, V’_1y y Rω₁ en términos de las velocidades iniciales V_0y, V_0x y Rω₀

${\displaystyle \begin{array}{l}{V}_{1x}=-\epsilon V_{0x}\\ V{\text{'}}_{1y}=\frac{1}{1+\gamma }\left((1-\gamma \beta )V_{0y}-\gamma (1+\beta )R{\omega }_0\right)\\ R{\omega }_1=\frac{1}{1+\gamma }\left(-(1+\beta )V_{0y}-(\beta -\gamma )R{\omega }_0\right)\end{array}}$

Cuando β=1 y ε=1, las ecuaciones se reducen al choque elástico.

Tiro parabólico

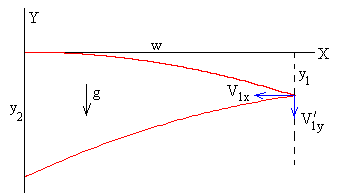
La pelota con su centro en la posición

${\displaystyle x=w{y}_1=-\frac{1}{2}g{\left(\frac{w}{V_{0x}}\right)}^2}$

se lanza con velocidad inicial V_1x y V’_1y hacia la pared izquierda del canal. Las ecuaciones del movimiento del centro de la pelota son

${\displaystyle \begin{array}{l}{V}_{1y}=V{\text{'}}_{1y}-gt\\ y=y_1+V{\text{'}}_{1y}t-\frac{1}{2}g{t}^{2}x=w+V_{1x}t\end{array}}$

La pelota choca con la pared izquierda cuando su centro se desplaza a la posición x=0 de modo que, la posición y velocidad de la pelota inmediatamente antes del segundo choque son

${\displaystyle \begin{array}{l}{V}_{1x}=V{\text{'}}_{1x}-g\left(\frac{-w}{V_{1x}}\right)\\ y_2=y_1+V{\text{'}}_{1y}\left(\frac{-w}{V_{1x}}\right)-\frac{1}{2}g{\left(\frac{-w}{V_{1x}}\right)}^2\end{array}}$

Choque de la pelota con la pared vertical izquierda

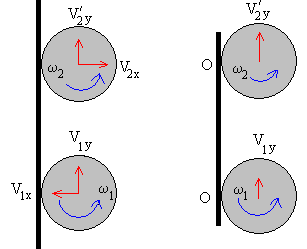
1. La componente de la velocidad perpendicular a la superficie cambia de módulo y sentido después del choque.

${\displaystyle V_{2x}=-\epsilon V_{1x}}$

2. La conservación del momento angular respecto de O se escribe

${\displaystyle \begin{array}{l}m{V}_{1y}R+I{\omega }_1=mV{\text{'}}_{2y}R+I{\omega }_2\\ V_{1y}+\gamma R{\omega }_1=V{\text{'}}_{2y}+\gamma R{\omega }_2\\ V{\text{'}}_{2y}-V_{1y}=\gamma R\left({\omega }_1-{\omega }_2\right)\end{array}}$

3. Las velocidades del punto de contacto O inmediatamente antes y después del choque están relacionadas

V’_2y-ω₂R=-β(V_1y-ω₁R)

Después del segundo choque, obtenemos V_2x, V’_2y y Rω₂ en términos de las velocidades V_1x, V_1y y Rω₁

${\displaystyle \begin{array}{l}{V}_{2x}=-\epsilon V_{1x}\\ V{\text{'}}_{2y}=\frac{1}{1+\gamma }\left((1-\gamma \beta )V_{1y}+\gamma (1+\beta )R{\omega }_1\right)\\ R{\omega }_2=\frac{1}{1+\gamma }\left((1+\beta )V_{1y}-(\beta -\gamma )R{\omega }_1\right)\end{array}}$

Tiro parabólico

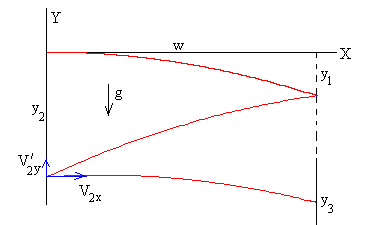
La pelota parte de la posición x=0, y₂ con velocidad V_2x, V’_2y hacia la pared derecha

${\displaystyle \begin{array}{l}{V}_{2y}=V{\text{'}}_{2y}-gt\\ y=y_2+V{\text{'}}_{2y}t-\frac{1}{2}g{t}^{2}x=V_{2x}t\end{array}}$

y así, se vuelve a repetir el movimiento

Ejemplos:

Choque elástico

• Coeficiente de restitución normal, ε=1
• Coeficiente de restitución tangencial, β=1
• La pelota es una esfera homogénea de radio R, γ=2/5

Choque con la pared derecha, x=1.0

${\displaystyle \begin{array}{l}{V}_{1x}=-V_{0x}\\ V{\text{'}}_{1y}=\frac{1}{7}\left(3V_{0y}-4R{\omega }_0\right)R{\omega }_1=\frac{1}{7}\left(-10V_{0y}-3R{\omega }_0\right)\end{array}}$ (1)

Choque con la pared izquierda, x=0

${\displaystyle \begin{array}{l}{V}_{2x}=-V_{1x}\\ V{\text{'}}_{2y}=\frac{1}{7}\left(3V_{1y}+4R{\omega }_1\right)R{\omega }_2=\frac{1}{7}\left(10V_{1y}-3R{\omega }_1\right)\end{array}}$ (2)

• Velocidades iniciales V_0x=5.5, V_0y=0, Rω₀=0 en el origen x=0, y=0
• Máximo desplazamiento horizontal del centro de la pelota, w=1.0

Etapas del movimiento

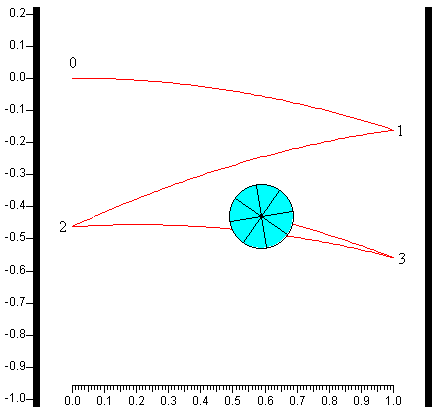
1. Tiro parabólico desde el origen a la posición de choque con la pared derecha

Tiempo de choque, t=w/V_0x=1/5.5

Posición del choque con la pared y velocidad inmediatamente antes del choque

${\displaystyle \begin{array}{l}{x}_1=1.0\text{m}{y}_1=-\frac{1}{2}g{\left(\frac{w}{V_{0x}}\right)}^2=-0.16\text{m}\\ V_{0x}=5.5\text{m/s}{V}_{0y}=-g\left(\frac{w}{V_{0x}}\right)=-1.78\text{m/s}\end{array}}$

2. Choque con la pared derecha, x=1

Aplicamos las fórmulas (1)

V_1x=-5.5 m/s, V’_1y=-0.76 m/s, Rω₁=2.55 m/s

3. Tiro parabólico desde la posición de choque 1 a la posición de choque 2 con la pared izquierda

Tiempo de choque, t=-w/V_1x=1/5.5

Posición y velocidad inmediatamente antes del choque

${\displaystyle \begin{array}{l}{V}_{1x}=-5.5\text{m/s}{V}_{1y}=V{\text{'}}_{1y}-g\left(\frac{-w}{V_{1x}}\right)=-2.55\text{m/s}\\ x_1=0.0\text{m}{y}_2=y_1+V{\text{'}}_{1y}\left(\frac{-w}{V_{1x}}\right)-\frac{1}{2}g{\left(\frac{-w}{V_{1x}}\right)}^2=-0.46\text{m}\end{array}}$

4. Choque con la pared izquierda, x=0

Aplicamos las fórmulas (2)

V_2x=5.5 m/s, V’_2y=0.3 6 m/s, Rω₂=-4.73 m/s

5. Tiro parabólico desde la posición de choque 2 a la posición de choque 3 con la pared derecha.

Tiempo de choque, t=w/V_2x=1/5.5

Posición y velocidad inmediatamente antes del choque

${\displaystyle \begin{array}{l}{V}_{2x}=5.5\text{m/s}{V}_{2y}=V{\text{'}}_{2y}-g\left(\frac{w}{V_{2x}}\right)=-1.42\text{m/s}\\ x_1=1.0\text{m}{y}_3=y_2+V{\text{'}}_{2y}\left(\frac{w}{V_{2x}}\right)-\frac{1}{2}g{\left(\frac{w}{V_{2x}}\right)}^2=-0.56\text{m}\end{array}}$

6. Choque con la pared derecha, x=1

Aplicamos las fórmulas (1)

V_3x=-5.5 m/s, V’_3y=2.09 m/s, Rω₃=4.05 m/s

Y así, sucesivamente.

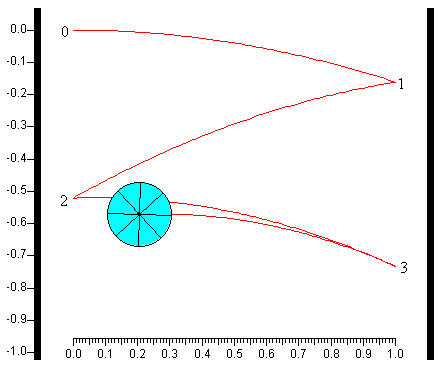
En la figura, se representa la trayectoria seguida por el centro de la pelota tras sucesivos rebotes.

Choque inelástico

• Coeficiente de restitución normal, ε=0.9
• Coeficiente de restitución tangencial, β=0.95
• La pelota es una esfera homogénea de radio R, γ=2/5

Choque con la pared derecha, x=1.0

${\displaystyle \begin{array}{l}{V}_{1x}=-0.9·V_{0x}\\ V{\text{'}}_{1y}=\frac{5}{7}\left(0.62·V_{0y}-0.78·R{\omega }_0\right)R{\omega }_1=\frac{5}{7}\left(-1.95·V_{0y}-0.55·R{\omega }_0\right)\end{array}}$ (1)

Choque con la pared izquierda, x=0

${\displaystyle \begin{array}{l}{V}_{2x}=-0.95·V_{1x}\\ V{\text{'}}_{2y}=\frac{5}{7}\left(0.62·V_{1y}+0.78·R{\omega }_1\right)R{\omega }_2=\frac{5}{7}\left(1.95·V_{1y}-0.55·R{\omega }_1\right)\end{array}}$ (2)

• Velocidades iniciales V_0x=5.5, V_0y=0, Rω₀=0 en el origen x=0, y=0
• Máximo desplazamiento horizontal del centro de la pelota, w=1.0

Etapas del movimiento

1. Tiro parabólico desde el origen a la posición de choque con la pared derecha

Tiempo de choque, t=w/V_0x=1/5.5

Posición del choque con la pared y velocidad inmediatamente antes del choque

${\displaystyle \begin{array}{l}{x}_1=1.0\text{m}{y}_1=-\frac{1}{2}g{\left(\frac{w}{V_{0x}}\right)}^2=-0.16\text{m}\\ V_{0x}=5.5\text{m/s}{V}_{0y}=-g\left(\frac{w}{V_{0x}}\right)=-1.78\text{m/s}\end{array}}$

2. Choque con la pared derecha, x=1

Aplicamos las fórmulas (1)

V_1x=-4.95 m/s, V’_1y=-0.79 m/s, Rω₁=2.48 m/s

3. Tiro parabólico desde la posición de choque 1 a la posición de choque 2 con la pared izquierda

Tiempo de choque, t=-w/V_1x=1/4.95

Posición y velocidad inmediatamente antes del choque

${\displaystyle \begin{array}{l}{V}_{1x}=-4.95\text{m/s}{V}_{1y}=V{\text{'}}_{1y}-g\left(\frac{-w}{V_{1x}}\right)=-2.77\text{m/s}\\ x_1=0.0\text{m}{y}_2=y_1+V{\text{'}}_{1y}\left(\frac{-w}{V_{1x}}\right)-\frac{1}{2}g{\left(\frac{-w}{V_{1x}}\right)}^2=-0.52\text{m}\end{array}}$

4. Choque con la pared izquierda, x=0

Aplicamos las fórmulas (2)

V_2x=4.46 m/s, V’_2y=0.16 m/s, Rω₂=-4.83 m/s

5. Tiro parabólico desde la posición de choque 2 a la posición de choque 3 con la pared derecha.

Tiempo de choque, t=w/V_2x=1/4.46

Posición y velocidad inmediatamente antes del choque

${\displaystyle \begin{array}{l}{V}_{2x}=4.46\text{m/s}{V}_{2y}=V{\text{'}}_{2y}-g\left(\frac{w}{V_{2x}}\right)=-2.04\text{m/s}\\ x_1=1.0\text{m}{y}_3=y_2+V{\text{'}}_{2y}\left(\frac{w}{V_{2x}}\right)-\frac{1}{2}g{\left(\frac{w}{V_{2x}}\right)}^2=-0.73\text{m}\end{array}}$

6. Choque con la pared derecha, x=1

Aplicamos las fórmulas (1)

V_3x=-4.0 m/s, V’_3y=1.79 m/s, Rω₃=4.74 m/s

Y así, sucesivamente.

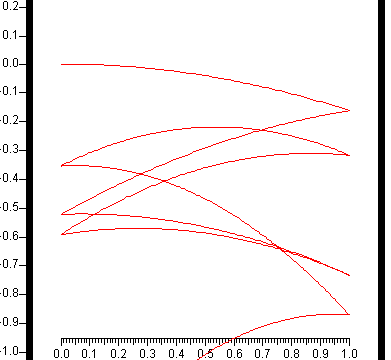
En la figura, se representa la trayectoria seguida por el centro de la pelota tras sucesivos rebotes.

Actividades

Se introduce

• El coeficiente de restitución normal ε, actuando en la barra de desplazamiento titulada Restitución.
• El coeficiente de restitución tangencial β, actuando en la barra de desplazamiento titulada Coef. beta.
• La velocidad angular inicial de rotación ω₀R, en el control de edición titulado Rotación w·R
• La pelota es una esfera homogénea cuyo momento de inercia es I=(2/5)mR², por lo que γ=2/5.
• El máximo desplazamiento horizontal del centro de la pelota es w=1.0

Se pulsa el botón titulado Empieza

Observar la trayectoria seguida por el centro de la pelota y calcular las posiciones y velocidades en cada rebote

Referencias

Hefner B. T. The kinematics of a superball bouncing between two vertical surfaces. Am. J. Phys. 72 (7) July 2004, pp. 875-883

Curso Interactivo de Física en Internet © Ángel Franco García