Equilibrio de una barra
Supongamos una barra de masa despreciable, que está sujeta por su extremo
O.
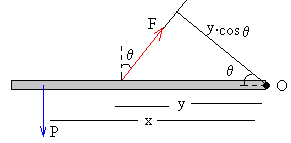
Si colocamos un peso P a una distancia x del origen. El momento de esta fuerza respecto del origen O es +P·x.
Atamos una cuerda a una distancia y del origen, y tiramos de ella haciendo un ángulo θ con la vertical, tal como se muestra en la figura. El momento de la fuerza F respecto del origen es -F·y·cosθ.
Para que la barra esté en equilibrio, el momento total deberá ser nulo.
-F·y·cosθ+P·x=0
Actividades
Sea una barra de 50 cm de longitud, de masa despreciable, dispone de ganchos situados en las divisiones 0, 5, 10, ... 50 cm. La barra está sujeta por uno de sus extremos O.
Se introduce
- La posición y de la cuerda, actuando sobre la barra de desplazamiento titulada Posición cuerda
- El ángulo θ que forma la cuerda con la vertical, actuando sobre la barra de desplazamiento titulada Angulo cuerda.
Se pulsa el botón titulado Nuevo
Aparecen pesas de distintos colores de 10 g, 25 g y 50 g . Con el puntero del ratón arrastramos una pesa y la colgamos de la barra en alguno de los ganchos.
Cogemos otra pesa y la colgamos de otro gancho de la barra y así, sucesivamente, hasta un máximo de seis pesas (dos de cada tipo). Podemos colgar más de una pesa en la misma posición, una debajo de la otra.
Un dinamómetro nos mide la tensión F de la cuerda necesaria para mantener la barra horizontal y en equilibrio. La fuerza viene expresada en Newton (N).
- Primero, establecemos el ángulo de la cuerda θ=0, y probamos con una sola pesa colocándola en varias posiciones y anotamos la fuerza que señala el dinamómetro.
Se pulsa el botón titulado Nuevo, se coloca una pesa colgada de un gancho, se apunta el valor de la fuerza F que marca el dinamómetro. Se pulsa el botón Nuevo, se elige la misma pesa y se coloca en otro gancho y así sucesivamente.
Fijarse que las pesas situadas en el origen no ejercen momento alguno. Y aquellas que están situadas en el otro extremo de la barra ejercen un momento máximo.
- Después, probamos con varias pesas en distintas posiciones coincidentes o no.
Ejemplo:
Colocamos las seis pesas tal como se muestra en la figura. Atamos un extremo de la cuerda en la posición y=30, formando un ángulo θ=60º con la vertical. Calcular la tensión F de la cuerda para que la barra se mantenga en posición horizontal y en equilibrio.
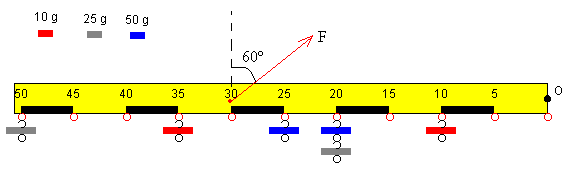
Pesa (g) Posición (cm) Momento (g·cm) 10 35 10 450 25 50 20 1750 50 25 20 2250 Total 4450
El momento de la fuerza que ejerce la cuerda es
-F·y·cosθ=-F·30·cos60º=-F·15
La condición de equilibrio se escribe
-F·15+4450=0 F=296.67 g
Expresamos la fuerza en N multiplicando por 9.8 y dividiendo por 1000
F=2.91 N
Se arrastra las pesas con el puntero del ratón y situarlas en las posiciones señaladas
en la regla