• Inicio
• Sólido rígido
• Movimiento general

Caja situada sobre un plano inclinado

El rozamiento requiere dos superficies de sólidos en contacto y en movimiento relativo. Sin embargo, bajo el nombre de fuerzas de rozamiento, se describen fuerzas de muy distinta naturaleza:

En la página titulada "Movimiento vertical de una esfera en el seno de un fluido", hemos estudiado las fuerzas de rozamiento que se oponen al movimiento de un cuerpo en el seno de un fluido viscoso. La fórmula de la fuerza depende del número de Reynolds.

En la página titulada "El rozamiento por deslizamiento" hemos estudiado el comportamiento de un cuerpo que descansa sobre un plano horizontal:

• Cuando la fuerza de rozamiento F_r estática no supera el valor máximo μ_sN el cuerpo permanece en reposo sobre la superficie.
• Sin embargo, cuando las dos superficies en contacto están en movimiento relativo la fuerza de rozamiento toma el valor F_r=μ_kN.

En la página titulada "Movimiento de rodar en un plano inclinado" en el apartado que estudia el movimiento de rodar sin deslizar, la fuerza de rozamiento estática aplicada en el punto de contacto entre la rueda y la superficie cuya velocidad en cada instante es cero. Dicha fuerza de rozamiento no realiza trabajo neto, y tanto su módulo como su sentido vienen determinados por las ecuaciones del movimiento.

Finalmente, en la página titulada "Deformaciones de la rueda y del plano horizontal"  cuando un sólido, por ejemplo, una bola de billar que rueda sobre una superficie, el sólido y la superficie se deforman alrededor del área de contacto, como consecuencia la bola va reduciendo su velocidad. Esta pérdida se debe a que los sólidos en contacto no son perfectamente elásticos.

Hemos estudiado varios ejemplos de discos rodando sobre planos horizontales e inclinados, en ellos hemos puesto de manifiesto el papel crucial que juega la fuerza de rozamiento como fuente de acoplamiento entre el movimiento de traslación y el de rotación.

La característica más importante de la situación que se estudia en esta página, es la gran riqueza de comportamientos en comparación con la esfera o un disco que se deja en reposo sobre un plano inclinado.

Ecuaciones del movimiento

Consideremos una caja de anchura b y altura h, de masa m , situada sobre un plano inclinado de ángulo θ .

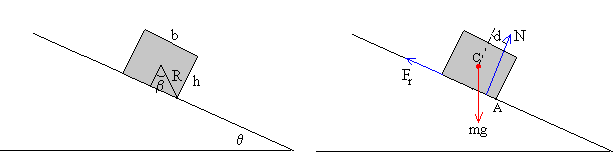
La caja está caracterizada por dos parámetros su anchura b y su altura h (se ignora la dimensión perpendicular al plano de la figura) o bien, por el ángulo β  y por la distancia R de un vértice al centro de la caja.

${\displaystyle \tan \beta =\frac{b}{h}R=\frac{1}{2}\sqrt{b^2+h^2}}$

Las fuerzas que actúan sobre la caja se muestran en la figura de la derecha:

• El peso mg que actúa en el centro de masas,
• La reacción del plano N, que no pasa en general, por el centro de masas  La distancia entre la dirección de dicha fuerza y el c.m. lo designamos por d.
• Finalmente, la fuerza de rozamiento F_r que actúa en la superficie de contacto entre la caja y el plano inclinado.

La fuerza de rozamiento F_r es una incógnita en las ecuaciones del movimiento. Adquiere su valor máximo μ_s·N cuando el cuerpo va a empezar a deslizar, donde μ_s es el coeficiente de rozamiento estático. Cuando el cuerpo desliza el valor de F_r cambia a μ_k·N. Para simplificar nuestro estudio supondremos que ambos coeficientes tienen el mismo valor μ .

Como es habitual en los problemas con planos inclinados, establecemos un sistema de ejes de modo que el eje Y es perpendicular al plano inclinado, y el eje X es paralelo al plano inclinado

Las ecuaciones del movimiento son las siguientes:

• Movimiento de traslación del c.m.

N-mgcosθ=ma_cy
mgsinθ-F_r=ma_cx

donde a_cx y a_cy son las componentes de la aceleración del centro de masas (c.m.)

• Movimiento de rotación alrededor de un eje perpendicular al plano de la figura y que pasa por el c.m.

${\displaystyle F_r\frac{h}{2}-Nd=\frac{1}{3}m{R}^2\alpha }$

El término mR²/3 es el momento de inercia de la caja respecto de un eje perpendicular al plano de la figura y que pasa por el c.m..

${\displaystyle I_c=\frac{1}{12}m(b^2+h^2)=\frac{1}{3}m{R}^2}$

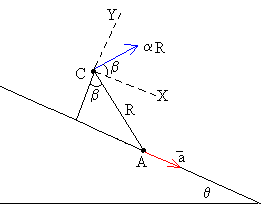Vamos a expresar la aceleración de c.m. ac en términos de la aceleración a del vértice A de la caja y de la aceleración angular α . acx=a+αRcosβ acy=αRsinβ

Las ecuaciones del movimiento serán por tanto,

${\displaystyle \begin{array}{l}N-mg\cos \theta =m\alpha R\text{sin}\beta \\ mg\text{sin}\theta -F_r=ma+m\alpha R\cos \beta \\ F_r\frac{h}{2}-Nd=\frac{1}{3}m{R}^2\alpha \end{array}}$

Vamos a estudiar los distintos casos que se pueden presentar cuando colocamos una caja de dimensiones b (base) y h (altura) en reposo sobre el plano inclinado.

1.-No desliza y no vuelca,

La caja permanece en reposo sobre el plano inclinado por lo que a=0, y α =0. A partir de estos dos datos, que introducimos en las tres ecuaciones se despejan las incógnitas

N=mgcosθ
F_r=mgsinθ
d=(h/2)·tanθ

La fuerza de rozamiento es inferior a su valor máximo, F_r≤ μ ·N, esta condición es equivalente a tanθ ≤ μ .

La reacción del plano N no puede salirse de la base de la caja d≤ b/2, lo que equivale a que tanθ ≤ tanβ .

2.-Desliza, pero no vuelca

Si desliza la aceleración ya no es nula a≥ 0, pero al no volcar la aceleración angular es nula α =0. Al deslizar, la fuerza de rozamiento tiene el valor F_r=μ ·N. A partir de estos dos datos, que introducimos en las tres ecuaciones se despejan las incógnitas

N=mg·cosθ
a=g(sinθ-μcosθ)=g·cosθ(tanθ-μ)
μ·N·h/2-N·d=0, por lo que  d=μh/2

La reacción del plano N no puede salirse de la base de la caja d≤ b/2, lo que equivale a que μ ≤ tanβ .

La condición de que la aceleración a sea positiva a≥ 0 equivale a μ ≤ tanθ .

3.-Vuelca, pero no desliza

Si no desliza la aceleración es nula, a=0, y si vuelca la aceleración angular no es nula α ≥ 0. La reacción del plano N se encontrará en el único punto de contacto A, de modo que d=b/2. En este caso, el valor de la fuerza de rozamiento F_r es desconocido, pero para que el punto A no deslice, se tiene que cumplir que F_r≤ μ ·N

A partir de estos dos datos, que introducimos en las tres ecuaciones se despejan las incógnitas

${\displaystyle \begin{array}{l}N-mg\cos \theta =m\alpha R\text{sin}\beta \\ mg\text{sin}\theta -F_r=m\alpha R\cos \beta \\ F_r\frac{h}{2}-N\frac{b}{2}=\frac{1}{3}m{R}^2\alpha \end{array}}$

Despejamos F_r en la segunda ecuación, N en la primera e introducimos sus expresiones en la tercera y teniendo en cuenta que h/2=R·cosβ, y b/2=R·sinβ

${\displaystyle \begin{array}{l}\alpha =\frac{3g}{4R}\text{sin}\left(\theta -\beta \right)\\ N=mg\cos \theta +\frac{3mg}{4}\text{sin}\beta \text{sin}\left(\theta -\beta \right)=\frac{3}{4}mg\cos \theta \left(\frac{1}{3}+{\cos }^2\beta +\text{sin}\beta \cos \beta \tan \theta \right)\\ F_r=mg\text{sin}\theta -\frac{3mg}{4}\cos \beta \text{sin}\left(\theta -\beta \right)=\frac{3}{4}mg\cos \theta \left(\left(\frac{1}{3}+{\text{sin}}^2\beta \right)\tan \theta +\text{sin}\beta \cos \beta \right)\end{array}}$

1. La condición de que la aceleración angular sea positiva α ≥ 0 equivale a tanθ≥ tanβ .

2. La condición de que el punto A no deslice F_r≤μ·N, equivale a

${\displaystyle \mu \ge \frac{\left(\frac{1}{3}+{\text{sin}}^2\beta \right)\tan \theta +\text{sin}\beta \cos \beta }{\frac{1}{3}+\cos \beta \text{sin}\beta \tan \theta +{\cos }^2\beta }}$

4.-Vuelca y desliza

Si desliza la aceleración no es nula, a≥ 0, y si vuelca la aceleración angular no es nula α ≥ 0. La reacción del plano N se encontrará en el único punto de contacto A, de modo que d=b/2. Al deslizar, la fuerza de rozamiento toma el valor  F_r=μ ·N

A partir de estos dos datos, que introducimos en las tres ecuaciones, se despejan las incógnitas

${\displaystyle \begin{array}{l}N-mg\cos \theta =m\alpha R\text{sin}\beta \\ mg\text{sin}\theta -F_r=ma+m\alpha R\cos \beta \\ F_r\frac{h}{2}-N\frac{b}{2}=\frac{1}{3}m{R}^2\alpha \end{array}}$

Se despeja N de la primera ecuación en función de α, se calcula F_r=μ·N en función de α. Se despeja α en la tercera ecuación. Se calcula N y a en la primera y en la segunda ecuación a partir de la expresión de α, y teniendo en cuenta que h/2=R·cosβ b/2=R·sinβ

${\displaystyle \begin{array}{l}\alpha =\frac{g}{R}\left(\frac{\cos \theta \left(\mu \cos \beta -\text{sin}\beta \right)}{\frac{1}{3}+{\text{sin}}^{\text{2}}\beta -\mu \text{sin}\beta \cos \beta }\right)\\ a=g\cos \theta \left(\tan \theta +\frac{\text{sin}\beta \cos \beta -\mu \left(\frac{1}{3}+{\cos }^2\beta \right)}{\frac{1}{3}+{\text{sin}}^2\beta -\mu \text{sin}\beta \cos \beta }\right)\\ N=mg\cos \theta \left(\frac{\frac{1}{3}}{\frac{1}{3}+{\text{sin}}^2\beta -\mu \text{sin}\beta \cos \beta }\right)\end{array}}$

1. Las condiciones de que N≥ 0, α ≥ 0 equivalen a

${\displaystyle \begin{array}{l}\mu \le \frac{\frac{1}{3}}{\text{sin}\beta \cos \beta }+\tan \beta ={\mu }^0\\ \tan \beta \le \mu \end{array}}$

1. La condición a≥0 nos lleva a

${\displaystyle \mu \le \frac{\left(\frac{1}{3}+{\text{sin}}^2\beta \right)\tan \theta +\text{sin}\beta \cos \beta }{\frac{1}{3}+\cos \beta \text{sin}\beta \tan \theta +{\cos }^2\beta }}$

Regiones del espacio (tanθ , μ )

Las desigualdades en cada uno de los cuatro casos definen en el espacio (tanθ , μ ), cuatro regiones que hemos pintado de distintos colores. Las abscisas son las tangentes de los ángulos θ del plano inclinado, las ordenadas son los valores del coeficiente de rozamiento μ. En el eje horizontal y vertical marcamos el valor de tanβ .

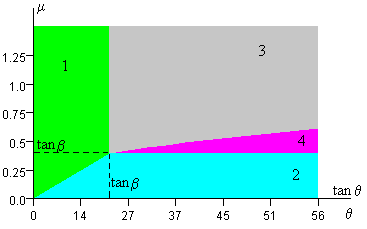
1. No desliza y no vuelca (región verde). Corresponde a la región definida por las desigualdades

1. tanθ ≤ μ .
2. tanθ ≤ tanβ

2. Desliza pero no vuelca (región azul). Corresponde a la región definida por las desigualdades

μ ≤ tanβ .
μ ≤ tanθ .

El espacio que queda se divide en dos regiones separadas por la curva μ_l en función de tanθ

${\displaystyle {\mu }_l=\frac{\left(\frac{1}{3}+{\text{sin}}^2\beta \right)\tan \theta +\text{sin}\beta \cos \beta }{\cos \beta \text{sin}\beta \tan \theta +\frac{1}{3}+{\cos }^2\beta }}$

cuya representación gráfica es

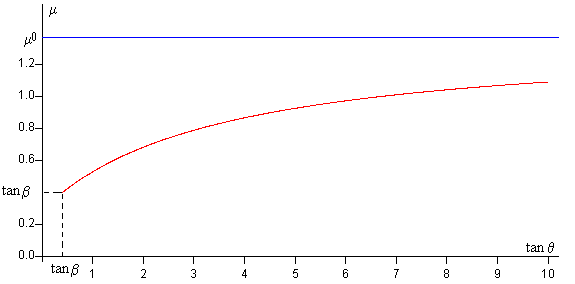
Esta curva pasa por el punto (tanβ , tanβ ) y tiene la forma

${\displaystyle y=\frac{ax+b}{cx+d}x\equiv \tan \theta \text{y}\equiv \mu }$

$\mathrm{Cuando\; x}\to \infty$ entonces $y\to a/c$. Cuando $\tan \theta \to \infty$ entonces $\mu \to {\mu }^0$

${\displaystyle {\mu }^0=\frac{\left(\frac{1}{3}+{\text{sin}}^2\beta \right)}{\cos \beta \text{sin}\beta }=\frac{\frac{1}{3}}{\text{sin}\beta \cos \beta }+\tan \beta }$

Por ejemplo, para una caja de dimensiones h=50 cm, y b=20 cm, tanβ=0.4. La asíntota horizontal es la recta μ=1.367

3. Vuelca (región gris)

La región "vuelca pero no desliza", está por encima de dicha curva, tal como expresa la desigualdad correspondiente

4. Desliza y vuelca (región en rojo)

La región "desliza y vuelca" está por debajo de dicha curva.

Ejemplo:

Por ejemplo, para una caja de dimensiones h=50 cm, y b=20 cm, tanβ=0.4, β=21.8º

• Coeficiente de rozamiento μ=0.5,
• Ángulo del plano inclinado θ=15º

Corresponde a la región 1 "No desliza y no vuelca": θ<β, tanθ<μ

• Coeficiente de rozamiento μ=0.2,
• Ángulo del plano inclinado θ=15º

Corresponde a la región 2 "Desliza y no vuelca": μ<tanβ, μ<tanθ

• Coeficiente de rozamiento μ=0.7,
• Ángulo del plano inclinado θ=40º

Para este ángulo, la curva μ_l que divide las regiones 3 y 4 vale

${\displaystyle {\mu }_l=\frac{\left(\frac{1}{3}+{\text{sin}}^{2}21.8\right)\tan 40+\text{sin}21.8\cos 21.8}{\cos 21.8\text{sin}21.8\tan 40+\frac{1}{3}+{\cos }^{2}21.8}=0.5}$

Corresponde a la región 3 "No desliza y vuelca": tanθ≥ tanβ, μ>0.5, por encima de la curva

• Coeficiente de rozamiento μ=0.45
• Ángulo del plano inclinado θ=40º

${\displaystyle {\mu }^0=\frac{\frac{1}{3}}{\text{sin}21.8\cos 21.8}+\tan 21.8=1.367}$

Corresponde a la región 4 "Desliza y vuelca": tanβ<μ<0.5, por debajo de la curva.

Actividades

Se introduce

• La altura h de la caja, en el control de edición titulado Altura
• La anchura o longitud de la base b de la caja, en el control de edición titulado Anchura

Se pulsa el botón titulado Nuevo

El programa interactivo calcula el ángulo β , tal que tanβ =b/h. El valor máximo admisible del ánguloβ  es 50º. Un mensaje en la parte inferior izquierda del applet nos avisa si al introducir las dimensiones de la caja se supera este valor.

Se representan las cuatro regiones del espacio (tanθ, μ)

• El coeficiente de rozamiento μ , en el control de edición titulado Coef. Rozamiento
• El ángulo θ  del plano inclinado, en el control de edición titulado Ángulo

Se pulsa el botón titulado Empieza.

Se representa el punto (tanθ , μ ) en color negro sobre la representación gráfica de las cuatro regiones y vemos el comportamiento de la caja, dependiendo en qué región esté situado dicho punto.

Nota: la simulación no describe correctamente el movimiento de rotación de la caja alrededor del vértice A, se limita a dar los valores iniciales de la aceleración angular en el instante en el que se inicia el vuelco. El estudio del comportamiento de una caja cuando no descansa sobre el plano inclinado, sino que su base forma un cierto ángulo con éste, es bastante complicado ya que los valores de las aceleraciones cambian a medida que la caja gira alrededor del vértice A.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Nunes A. M., Silva J. P. Tiltled boxes on inclined planes. Am. J. Phys. 68, (11) November 2000, pp. 1042-1049

Curso Interactivo de Física en Internet © Ángel Franco García